22.2 相似三角形的判定 同步练习 2022-2023学年上学期安徽省九年级数学期末试题选编(含解析)
文档属性
| 名称 | 22.2 相似三角形的判定 同步练习 2022-2023学年上学期安徽省九年级数学期末试题选编(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 416.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览



文档简介
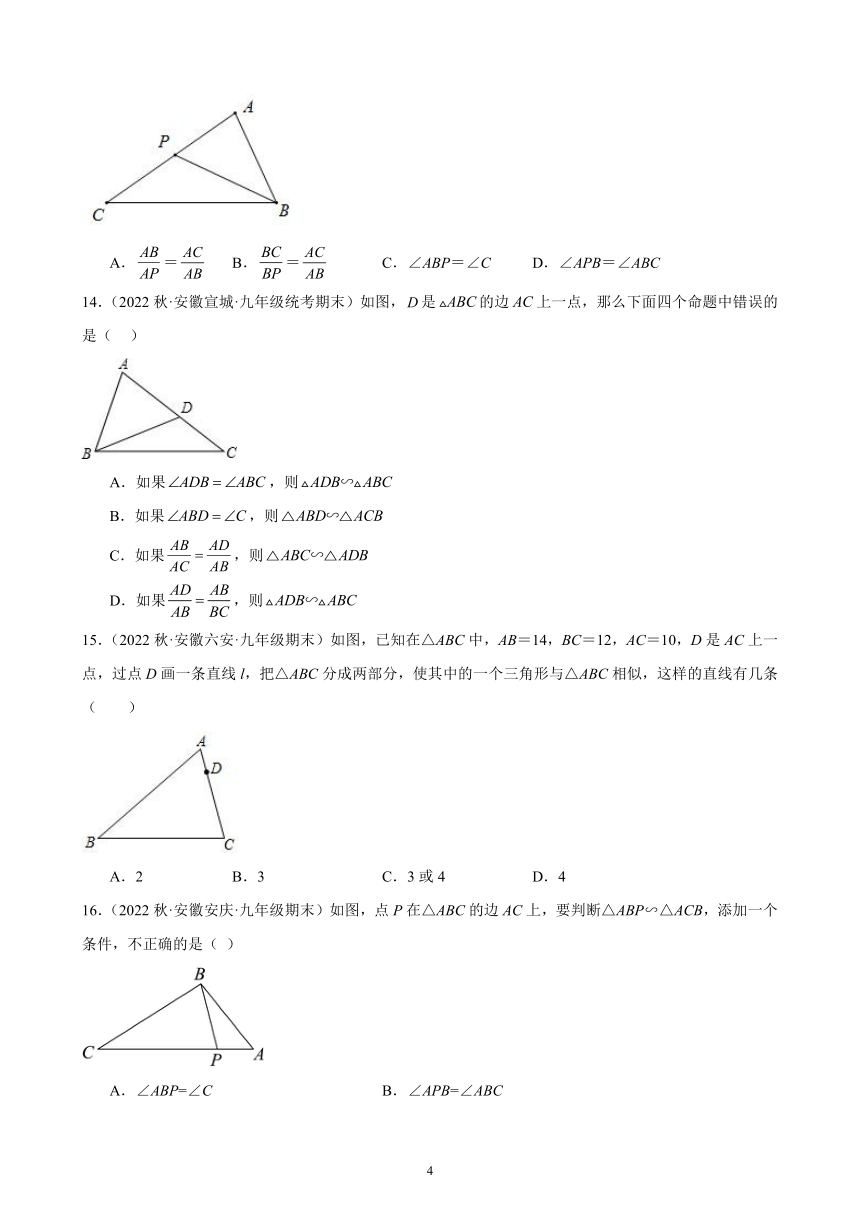
22.2 相似三角形的判定
一、单选题
1.(2022秋·安徽马鞍山·九年级期末)在和中,有下列条件:①;②;③;④,如果从中任取两个条件组成一组,那么能判断的共有( )
A.3组 B.4组 C.5组 D.6组
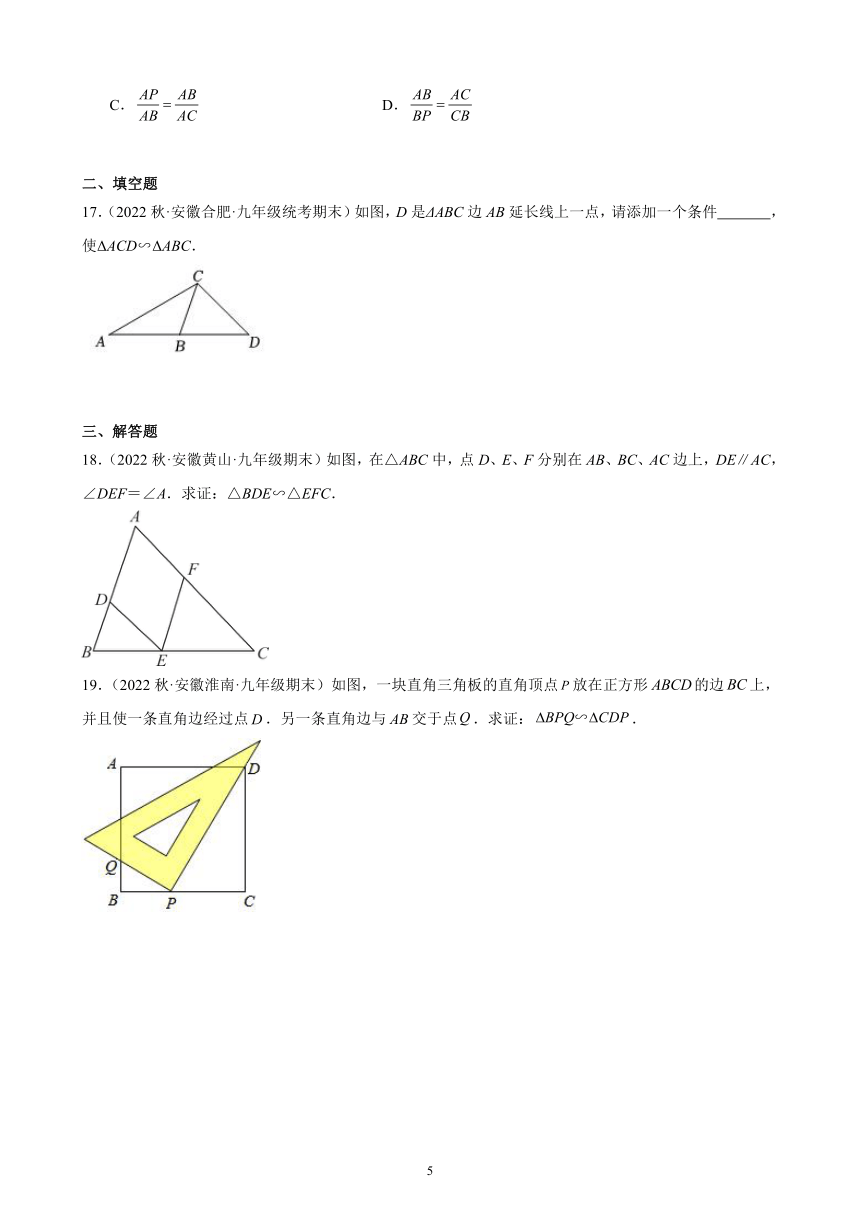
2.(2022秋·安徽宿州·九年级期末)下列各组条件中,一定能够判定△ABC与△DEF相似的是( )
A.∠A=∠B,∠D=∠E
B.∠B=∠E,AB=3,AC=4,DE:DF=3:4
C.△ABC三边长分别为6,18,21,△DEF三边之比为2:7:6
D.∠C=91°,∠E=91°,DE:AB=EF:AC
3.(2022秋·安徽安庆·九年级统考期末)如图所示,△ABC中∠BAC=80°,AB=4,AC=6.甲、乙、丙、丁四名同学分别在△ABC内画出一个阴影三角形与△ABC相似,其中画的错误的是( )
A. B.
C. D.
4.(2022秋·安徽宣城·九年级统考期末)如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是
A.B.C. D.
5.(2022秋·安徽六安·九年级统考期末)如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
6.(2022秋·安徽宣城·九年级统考期末)如图,点在的边上,要判断,添加下列一个条件,不正确的是( )
A. B. C. D.
7.(2022秋·安徽马鞍山·九年级期末)已知,如图∠DAB=∠CAE,下列条件中不能判断△DAE∽△BAC的是( )
A.∠D=∠B B.∠E=∠C C. D.
8.(2022秋·安徽合肥·九年级统考期末)如图,中,点是边上一点,下列条件中,不能判定与相似的是( )
A. B.
C. D.
9.(2022秋·安徽合肥·九年级统考期末)如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍然不能判定△ABC与△DAE相似的是( )
A.∠CAB=∠D B.AB:AC=AD:DE C.ADBC D.BC:AC=AD:AE
10.(2022秋·安徽蚌埠·九年级统考期末)在中,点D,E分别在边,上,则在下列条件中,不能使得以A,D,E为顶点的三角形与相似的是( )
A. B.
C. D.
11.(2022秋·安徽亳州·九年级统考期末)如图,在△ABC中,点D,E分别是AB,AC上的点,连接DE,下列条件不能使得△ABC与△ADE相似的是( )
A.∠ADE=∠ACB B.DE∥BC C. D.
12.(2022秋·安徽合肥·九年级统考期末)如图,CD是Rt△ABC斜边AB上的中线,过点C作CE⊥CD交AB的延长线于点E,添加下列条件仍不能判断△CEB与△CAD相似的是( )
A.∠CBA=2∠A B.点B是DE的中点
C.CE CD=CA CB D.=
13.(2022秋·安徽安庆·九年级统考期末)如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
14.(2022秋·安徽宣城·九年级统考期末)如图,是的边上一点,那么下面四个命题中错误的是( )
A.如果,则
B.如果,则
C.如果,则
D.如果,则
15.(2022秋·安徽六安·九年级期末)如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,这样的直线有几条( )
A.2 B.3 C.3或4 D.4
16.(2022秋·安徽安庆·九年级期末)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C. D.
二、填空题
17.(2022秋·安徽合肥·九年级统考期末)如图,D是ΔABC边AB延长线上一点,请添加一个条件 ,使ΔACD∽ΔABC.
三、解答题
18.(2022秋·安徽黄山·九年级期末)如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,∠DEF=∠A.求证:△BDE∽△EFC.
19.(2022秋·安徽淮南·九年级期末)如图,一块直角三角板的直角顶点放在正方形的边上,并且使一条直角边经过点.另一条直角边与交于点.求证:.
参考答案:
1.A
【分析】利用相似三角形的判定依次判断即可求解.
【详解】解:当时,;
当,时,;
当,时,;
综上所述:满足条件的组合为:①②、①④、③④,共3组,
故选:A.
【点睛】本题考查了相似三角形判定,掌握相似三角形的判定方法是解题的关键.
2.C
【分析】由题意直接根据相似三角形的判定方法进行分析判断即可得出答案.
【详解】解:A、∠A和∠B,∠D和∠E不是两个三角形的对应角,故不能判定两三角形相似,故此选项不符合题意;
B、根据∠B=∠E,不能判定两三角形相似,因为相等的两个角不是夹角,故此选项不符合题意;
C、△ABC三边长分别为6,21,18,则三边之比为2:7:6,由△DEF三边之比为2:7:6可知△ABC与△DEF相似,故此选项符合题意;
D、DE:AB=EF:AC不是直角三角形的对应边成比例,故不能判定两三角形相似,故此选项不符合题意.
故选:C.
【点睛】本题主要考查相似三角形的判定,解题的关键是掌握三角形相似的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.
3.D
【分析】通过相似三角形的判定方法分别对各选项进行判断.
【详解】A.满足两组角分别相等,则阴影三角形与△ABC相似;
B.满足两组角分别相等,则阴影三角形与△ABC相似;
C.满足两组边成比例且夹角相等,则阴影三角形与△ABC相似;
D.不满足相似三角形的判定方法.
故选D.
【点睛】考查了相似三角形的判定,解题关键是熟记相似三角形的判定方法.
4.B
【分析】根据网格的特点求出三角形的三边,再根据相似三角形的判定定理即可求解.
【详解】已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.
故选B.
【点睛】此题主要考查相似三角形的判定,解题的关键是熟知相似三角形的判定定理.
5.D
【分析】先根据求出,再根据相似三角形的判定方法解答.
【详解】解:,
,
、添加,可用两角法判定,故本选项错误;
、添加,可用两角法判定,故本选项错误;
、添加,可用两边及其夹角法判定,故本选项错误;
、添加,不能判定,故本选项正确;
故选:D.
【点睛】本题主要考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.
6.B
【分析】分别利用相似三角形的判定方法判断得出即可.
【详解】解:A.当时,又,
,故此选项不符合题意;
B.,但不知夹角是否相等,不能证明,故此选项符合题意;
C.当时,又,
,故此选项不符合题意;
D.当时,又,
,故此选项不符合题意;
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确把握判定方法是解题关键.
7.D
【分析】根据相似三角形的判定方法逐项分析即可.
【详解】解:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
∴∠DAE=∠BAC,
∴当添加条件∠D=∠B时,符合两角分别相等的两个三角形相似,则△DAE∽△BAC,故选项A不符合题意;
当添加条件∠E=∠C时,符合两角分别相等的两个三角形相似,则△DAE∽△BAC,故选项B不符合题意;
当添加条件时,符合两边成比例,且夹角相等的两个三角形相似,则△DAE∽△BAC,故选项C不符合题意;
当添加条件时,则△DAE和△BAC不一定相似,故选项D符合题意;
故选:D.
【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解答本题的关键.①两角分别相等的两个三角形相似;②两边成比例,且夹角相等的两个三角形相似;③三边成比例的两个三角形相似.
8.D
【分析】由图可知,∠B是△ABC与△ABD的公共角,所以再添加一组角相等或者添加夹∠B的两边成比例即可判断.
【详解】解:A.∵AB2=BD BC,
∴ ,
∵∠B=∠B,
∴△BAD∽△BCA,
故A不符合题意;
B.∵∠BDA=∠BAC,∠B=∠B,
∴△BAD∽△BCA,
故B不符合题意;
C.∵∠ADC=∠C+∠B,∠ADC=∠BAD+∠B,
∴∠C=∠BAD,
∵∠B=∠B,
∴△BAD∽△BCA,
故C不符合题意;
D.∵AD BC=AB AC,
∴,
∵∠B≠∠BAD,
∴不能判定△ABC与△ABD相似,
故选:D.
【点睛】本题考查了相似三角形的判定,结合图形分析并熟练掌握相似三角形的判定是解题的关键.
9.D
【分析】根据相似三角形的判定方法一一判断即可.
【详解】A.由∠C=∠AED=90°,∠CAB=∠D,可知△ACB∽△DEA,本选项不符合题意;
B.设,则AB=kAC,AD=kDE,,
∴,
∵∠C=∠AED=90°,
∴△ACB∽△DEA,本选项不符合题意;
C.由BCAD,可得∠B=∠DAE,由∠C=∠AED=90°,可得△ACB∽△DEA,本选项不符合题意;
D.由,无法判断三角形相似,本选项符合题意.
故选:D.
【点睛】本题考查相似三角形的判定,解题的关键是熟练掌握相似三角形的判定,属于中考常考题型.
10.C
【分析】根据题意画出图形,再由相似三角形的判定定理进行解答即可.
【详解】解:如图,
A、∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,故A不符合题意;
B、∵DE∥BC,
∴△ADE∽△ABC,故B不符合题意;
C、,不能使△ADE和△ABC相似,故C符合题意;
D、∵,∠A=∠A,
∴△ADE∽△ACB,故D不符合题意.
故选:C.
【点睛】此题考查了相似三角形的判定,属于基础题,关键是掌握相似三角形的几种判定定理.
11.C
【分析】根据相似三角形的判定方法逐一判断即可.
【详解】解:A.∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB,
故此选项不符合题意;
B.∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,
故此选项不符合题意;
C.∵,∠AED≠∠ABC,
∴△ABC与△ADE不相似,
故此选项符合题意;
D.∵,∠A=∠A,
∴△ADE∽△ACB,
故此选项不符合题意;
故选:C.
【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.
12.D
【分析】根据相似三角形的判定方法一一判断即可.
【详解】∵CE⊥CD,
∴∠EDC=90°,
∵∠BCA=90°,
∴∠BCE=∠DCA=90°-∠BCD,
∵CD是斜边AB上的中线,
∴DC=DB=DA,
∴∠DAC=∠A,
∴∠BCE=∠DCA=∠A,
∵∠CBA=2∠A,∠CBA+∠A=90°,
∴∠A=∠BCE=∠DCA=30°,∠CBA=60°,
∴∠E=∠CBA-∠BCE=30°,
∴∠BCE=∠DCA=∠E=∠A,
∴△CEB∽△CAD,
∴A不符合题意;
∵点B是DE的中点,
∴BE=BC,
∴∠BCE=∠E,
∴∠BCE=∠E=∠DCA=∠A,
∴△CEB∽△CAD,
∴B不符合题意;
∵CE CD=CA CB,
∴.
∵∠BCE=∠DCA,
∴△CEB∽△CAD,
∴C不符合题意;
由,由于∠E和∠A不能判断相等,故不能判断△CEB与△CAD相似,
∴D符合题意.
故选:D.
【点睛】本题考查判断三角形相似,直角三角形的性质.掌握判定三角形相似的条件是解题关键.
13.B
【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.
【详解】解:A、∵∠A=∠A,=∴△ABP∽△ACB,故本选项不符合题意;
B、根据=和∠A=∠A不能判断△ABP∽△ACB,故本选项符合题意;
C、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项不符合题意;
D、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项不符合题意;
故选:B.
【点睛】本题考查了相似的三角形的判定定理的应用,能正确运用判定定理进行推理是解此题的关键.
14.D
【分析】由两个角对应相等的两个三角形相似可判断,由两边对应成比例,且夹角相等可判断,从而可得答案.
【详解】解:A中∠ADB=∠ABC,∠A为公共角,所以,故A不符合题意;
B中∠ABD=∠C,∠A为公共角,所以,故B不符合题意;
C中对应边成比例,∠A为公共角,所以,故不符合题意;
D中对应边成比例,但夹角不相等,所以不一定相似,故符合题意.
故选:D.
【点睛】本题考查的是相似三角形的判定,掌握相似三角形的判定方法是解题的关键.
15.D
【分析】分别利用当DF∥BC时,当∠ADE=∠B时,当DN∥AB时,当∠CDM=∠B时求出相似三角形,进而得出答案.
【详解】解:如图所示:当DF∥BC时,则△AFD∽△ABC,
当∠ADE=∠B时,则△ADE∽△ABC,
当DN∥AB时,则△CDN∽△CAB,
当∠CDM=∠B时,则△CDM∽△CBA.
这样的直线可以画4条.
故选择:D.
【点睛】此题主要考查了相似三角形的判定,利用分类讨论得出相似三角形是解题关键.
16.D
【详解】解:A.当∠ABP=∠C时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
B.当∠APB=∠ABC时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
C.当时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
D.无法得到△ABP∽△ACB,故此选项正确.
故选:D.
17.AC=AB AD(答案不唯一)
【分析】根据相似三角形的判定添加适当的条件即可.
【详解】解: 添加:AC=AB AD
∵AC=AB AD
∴
∵∠A=∠A
∴ΔACD∽ΔABC.
故答案为:AC=AB AD(答案不唯一).
【点睛】本题考查相似三角形的判定,熟练掌握相似三角形的判定方法是解题的关键.
18.见解析
【分析】根据,得出,根据可判断,可证.
【详解】证明,
,
又,
,
,
,
.
【点睛】本题考查平行线性质,三角形相似判定,掌握平行线性质,三角形相似判定是解题关键.
19.详见解析
【分析】根据正方形性质得到角的关系,从而根据判定两三角形相似的方法证明△BPQ∽△CDP.
【详解】证明:四边形是正方形,
.
,
,,
,
.
【点睛】此题重点考查学生对两三角形相似的判定的理解,熟练掌握两三角形相似的判定方法是解题的关键.
一、单选题
1.(2022秋·安徽马鞍山·九年级期末)在和中,有下列条件:①;②;③;④,如果从中任取两个条件组成一组,那么能判断的共有( )
A.3组 B.4组 C.5组 D.6组
2.(2022秋·安徽宿州·九年级期末)下列各组条件中,一定能够判定△ABC与△DEF相似的是( )
A.∠A=∠B,∠D=∠E
B.∠B=∠E,AB=3,AC=4,DE:DF=3:4
C.△ABC三边长分别为6,18,21,△DEF三边之比为2:7:6
D.∠C=91°,∠E=91°,DE:AB=EF:AC
3.(2022秋·安徽安庆·九年级统考期末)如图所示,△ABC中∠BAC=80°,AB=4,AC=6.甲、乙、丙、丁四名同学分别在△ABC内画出一个阴影三角形与△ABC相似,其中画的错误的是( )
A. B.
C. D.
4.(2022秋·安徽宣城·九年级统考期末)如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC相似的是
A.B.C. D.
5.(2022秋·安徽六安·九年级统考期末)如图,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
6.(2022秋·安徽宣城·九年级统考期末)如图,点在的边上,要判断,添加下列一个条件,不正确的是( )
A. B. C. D.
7.(2022秋·安徽马鞍山·九年级期末)已知,如图∠DAB=∠CAE,下列条件中不能判断△DAE∽△BAC的是( )
A.∠D=∠B B.∠E=∠C C. D.
8.(2022秋·安徽合肥·九年级统考期末)如图,中,点是边上一点,下列条件中,不能判定与相似的是( )
A. B.
C. D.
9.(2022秋·安徽合肥·九年级统考期末)如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍然不能判定△ABC与△DAE相似的是( )
A.∠CAB=∠D B.AB:AC=AD:DE C.ADBC D.BC:AC=AD:AE
10.(2022秋·安徽蚌埠·九年级统考期末)在中,点D,E分别在边,上,则在下列条件中,不能使得以A,D,E为顶点的三角形与相似的是( )
A. B.
C. D.
11.(2022秋·安徽亳州·九年级统考期末)如图,在△ABC中,点D,E分别是AB,AC上的点,连接DE,下列条件不能使得△ABC与△ADE相似的是( )
A.∠ADE=∠ACB B.DE∥BC C. D.
12.(2022秋·安徽合肥·九年级统考期末)如图,CD是Rt△ABC斜边AB上的中线,过点C作CE⊥CD交AB的延长线于点E,添加下列条件仍不能判断△CEB与△CAD相似的是( )
A.∠CBA=2∠A B.点B是DE的中点
C.CE CD=CA CB D.=
13.(2022秋·安徽安庆·九年级统考期末)如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
14.(2022秋·安徽宣城·九年级统考期末)如图,是的边上一点,那么下面四个命题中错误的是( )
A.如果,则
B.如果,则
C.如果,则
D.如果,则
15.(2022秋·安徽六安·九年级期末)如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,这样的直线有几条( )
A.2 B.3 C.3或4 D.4
16.(2022秋·安徽安庆·九年级期末)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C. D.
二、填空题
17.(2022秋·安徽合肥·九年级统考期末)如图,D是ΔABC边AB延长线上一点,请添加一个条件 ,使ΔACD∽ΔABC.
三、解答题
18.(2022秋·安徽黄山·九年级期末)如图,在△ABC中,点D、E、F分别在AB、BC、AC边上,DE∥AC,∠DEF=∠A.求证:△BDE∽△EFC.
19.(2022秋·安徽淮南·九年级期末)如图,一块直角三角板的直角顶点放在正方形的边上,并且使一条直角边经过点.另一条直角边与交于点.求证:.
参考答案:
1.A
【分析】利用相似三角形的判定依次判断即可求解.
【详解】解:当时,;
当,时,;
当,时,;
综上所述:满足条件的组合为:①②、①④、③④,共3组,
故选:A.
【点睛】本题考查了相似三角形判定,掌握相似三角形的判定方法是解题的关键.
2.C
【分析】由题意直接根据相似三角形的判定方法进行分析判断即可得出答案.
【详解】解:A、∠A和∠B,∠D和∠E不是两个三角形的对应角,故不能判定两三角形相似,故此选项不符合题意;
B、根据∠B=∠E,不能判定两三角形相似,因为相等的两个角不是夹角,故此选项不符合题意;
C、△ABC三边长分别为6,21,18,则三边之比为2:7:6,由△DEF三边之比为2:7:6可知△ABC与△DEF相似,故此选项符合题意;
D、DE:AB=EF:AC不是直角三角形的对应边成比例,故不能判定两三角形相似,故此选项不符合题意.
故选:C.
【点睛】本题主要考查相似三角形的判定,解题的关键是掌握三角形相似的判定方法:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.
3.D
【分析】通过相似三角形的判定方法分别对各选项进行判断.
【详解】A.满足两组角分别相等,则阴影三角形与△ABC相似;
B.满足两组角分别相等,则阴影三角形与△ABC相似;
C.满足两组边成比例且夹角相等,则阴影三角形与△ABC相似;
D.不满足相似三角形的判定方法.
故选D.
【点睛】考查了相似三角形的判定,解题关键是熟记相似三角形的判定方法.
4.B
【分析】根据网格的特点求出三角形的三边,再根据相似三角形的判定定理即可求解.
【详解】已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.
故选B.
【点睛】此题主要考查相似三角形的判定,解题的关键是熟知相似三角形的判定定理.
5.D
【分析】先根据求出,再根据相似三角形的判定方法解答.
【详解】解:,
,
、添加,可用两角法判定,故本选项错误;
、添加,可用两角法判定,故本选项错误;
、添加,可用两边及其夹角法判定,故本选项错误;
、添加,不能判定,故本选项正确;
故选:D.
【点睛】本题主要考查了相似三角形的判定:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.
6.B
【分析】分别利用相似三角形的判定方法判断得出即可.
【详解】解:A.当时,又,
,故此选项不符合题意;
B.,但不知夹角是否相等,不能证明,故此选项符合题意;
C.当时,又,
,故此选项不符合题意;
D.当时,又,
,故此选项不符合题意;
故选:B.
【点睛】此题主要考查了相似三角形的判定,正确把握判定方法是解题关键.
7.D
【分析】根据相似三角形的判定方法逐项分析即可.
【详解】解:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
∴∠DAE=∠BAC,
∴当添加条件∠D=∠B时,符合两角分别相等的两个三角形相似,则△DAE∽△BAC,故选项A不符合题意;
当添加条件∠E=∠C时,符合两角分别相等的两个三角形相似,则△DAE∽△BAC,故选项B不符合题意;
当添加条件时,符合两边成比例,且夹角相等的两个三角形相似,则△DAE∽△BAC,故选项C不符合题意;
当添加条件时,则△DAE和△BAC不一定相似,故选项D符合题意;
故选:D.
【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定方法是解答本题的关键.①两角分别相等的两个三角形相似;②两边成比例,且夹角相等的两个三角形相似;③三边成比例的两个三角形相似.
8.D
【分析】由图可知,∠B是△ABC与△ABD的公共角,所以再添加一组角相等或者添加夹∠B的两边成比例即可判断.
【详解】解:A.∵AB2=BD BC,
∴ ,
∵∠B=∠B,
∴△BAD∽△BCA,
故A不符合题意;
B.∵∠BDA=∠BAC,∠B=∠B,
∴△BAD∽△BCA,
故B不符合题意;
C.∵∠ADC=∠C+∠B,∠ADC=∠BAD+∠B,
∴∠C=∠BAD,
∵∠B=∠B,
∴△BAD∽△BCA,
故C不符合题意;
D.∵AD BC=AB AC,
∴,
∵∠B≠∠BAD,
∴不能判定△ABC与△ABD相似,
故选:D.
【点睛】本题考查了相似三角形的判定,结合图形分析并熟练掌握相似三角形的判定是解题的关键.
9.D
【分析】根据相似三角形的判定方法一一判断即可.
【详解】A.由∠C=∠AED=90°,∠CAB=∠D,可知△ACB∽△DEA,本选项不符合题意;
B.设,则AB=kAC,AD=kDE,,
∴,
∵∠C=∠AED=90°,
∴△ACB∽△DEA,本选项不符合题意;
C.由BCAD,可得∠B=∠DAE,由∠C=∠AED=90°,可得△ACB∽△DEA,本选项不符合题意;
D.由,无法判断三角形相似,本选项符合题意.
故选:D.
【点睛】本题考查相似三角形的判定,解题的关键是熟练掌握相似三角形的判定,属于中考常考题型.
10.C
【分析】根据题意画出图形,再由相似三角形的判定定理进行解答即可.
【详解】解:如图,
A、∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,故A不符合题意;
B、∵DE∥BC,
∴△ADE∽△ABC,故B不符合题意;
C、,不能使△ADE和△ABC相似,故C符合题意;
D、∵,∠A=∠A,
∴△ADE∽△ACB,故D不符合题意.
故选:C.
【点睛】此题考查了相似三角形的判定,属于基础题,关键是掌握相似三角形的几种判定定理.
11.C
【分析】根据相似三角形的判定方法逐一判断即可.
【详解】解:A.∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB,
故此选项不符合题意;
B.∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,
故此选项不符合题意;
C.∵,∠AED≠∠ABC,
∴△ABC与△ADE不相似,
故此选项符合题意;
D.∵,∠A=∠A,
∴△ADE∽△ACB,
故此选项不符合题意;
故选:C.
【点睛】本题考查了相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.
12.D
【分析】根据相似三角形的判定方法一一判断即可.
【详解】∵CE⊥CD,
∴∠EDC=90°,
∵∠BCA=90°,
∴∠BCE=∠DCA=90°-∠BCD,
∵CD是斜边AB上的中线,
∴DC=DB=DA,
∴∠DAC=∠A,
∴∠BCE=∠DCA=∠A,
∵∠CBA=2∠A,∠CBA+∠A=90°,
∴∠A=∠BCE=∠DCA=30°,∠CBA=60°,
∴∠E=∠CBA-∠BCE=30°,
∴∠BCE=∠DCA=∠E=∠A,
∴△CEB∽△CAD,
∴A不符合题意;
∵点B是DE的中点,
∴BE=BC,
∴∠BCE=∠E,
∴∠BCE=∠E=∠DCA=∠A,
∴△CEB∽△CAD,
∴B不符合题意;
∵CE CD=CA CB,
∴.
∵∠BCE=∠DCA,
∴△CEB∽△CAD,
∴C不符合题意;
由,由于∠E和∠A不能判断相等,故不能判断△CEB与△CAD相似,
∴D符合题意.
故选:D.
【点睛】本题考查判断三角形相似,直角三角形的性质.掌握判定三角形相似的条件是解题关键.
13.B
【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.
【详解】解:A、∵∠A=∠A,=∴△ABP∽△ACB,故本选项不符合题意;
B、根据=和∠A=∠A不能判断△ABP∽△ACB,故本选项符合题意;
C、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项不符合题意;
D、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项不符合题意;
故选:B.
【点睛】本题考查了相似的三角形的判定定理的应用,能正确运用判定定理进行推理是解此题的关键.
14.D
【分析】由两个角对应相等的两个三角形相似可判断,由两边对应成比例,且夹角相等可判断,从而可得答案.
【详解】解:A中∠ADB=∠ABC,∠A为公共角,所以,故A不符合题意;
B中∠ABD=∠C,∠A为公共角,所以,故B不符合题意;
C中对应边成比例,∠A为公共角,所以,故不符合题意;
D中对应边成比例,但夹角不相等,所以不一定相似,故符合题意.
故选:D.
【点睛】本题考查的是相似三角形的判定,掌握相似三角形的判定方法是解题的关键.
15.D
【分析】分别利用当DF∥BC时,当∠ADE=∠B时,当DN∥AB时,当∠CDM=∠B时求出相似三角形,进而得出答案.
【详解】解:如图所示:当DF∥BC时,则△AFD∽△ABC,
当∠ADE=∠B时,则△ADE∽△ABC,
当DN∥AB时,则△CDN∽△CAB,
当∠CDM=∠B时,则△CDM∽△CBA.
这样的直线可以画4条.
故选择:D.
【点睛】此题主要考查了相似三角形的判定,利用分类讨论得出相似三角形是解题关键.
16.D
【详解】解:A.当∠ABP=∠C时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
B.当∠APB=∠ABC时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
C.当时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
D.无法得到△ABP∽△ACB,故此选项正确.
故选:D.
17.AC=AB AD(答案不唯一)
【分析】根据相似三角形的判定添加适当的条件即可.
【详解】解: 添加:AC=AB AD
∵AC=AB AD
∴
∵∠A=∠A
∴ΔACD∽ΔABC.
故答案为:AC=AB AD(答案不唯一).
【点睛】本题考查相似三角形的判定,熟练掌握相似三角形的判定方法是解题的关键.
18.见解析
【分析】根据,得出,根据可判断,可证.
【详解】证明,
,
又,
,
,
,
.
【点睛】本题考查平行线性质,三角形相似判定,掌握平行线性质,三角形相似判定是解题关键.
19.详见解析
【分析】根据正方形性质得到角的关系,从而根据判定两三角形相似的方法证明△BPQ∽△CDP.
【详解】证明:四边形是正方形,
.
,
,,
,
.
【点睛】此题重点考查学生对两三角形相似的判定的理解,熟练掌握两三角形相似的判定方法是解题的关键.
同课章节目录
