2023—2024学年人教版数学七年级上册1.2.3 相反数 课件(共26张PPT)
文档属性
| 名称 | 2023—2024学年人教版数学七年级上册1.2.3 相反数 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 06:33:22 | ||
图片预览





文档简介
(共26张PPT)
1.2.1 有理数
人教版· 数学· 七年级(上)
第一章 有理数
第3课时 相反数
1.借助数轴理解相反数的意义,了解数轴上表示相反数的两个点关于原点对称.
2.会求有理数的相反数.
学习目标
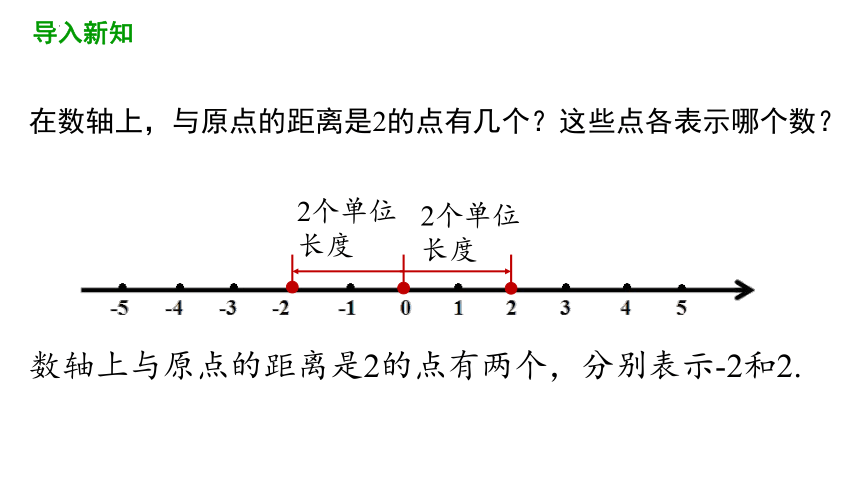
在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
数轴上与原点的距离是2的点有两个,分别表示-2和2.
2个单位长度
2个单位长度
导入新知
设a是一个正数,数轴上与原点的距离等于a(a为正数)的点有几个?这些点表示的数有什么关系?
如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右两侧,表示-a和a,我们说这两个点关于原点对称.
在数轴上与原点的距离是2的点有两个,分别表示的数是2和-2.
观察:
+ 2 - 2
只有符号不同
想一想:
在数轴上,距离原点4个单位长度的点所表示的数有几个?这些点各表示哪些数?
-4 -3 -2 -1 0 1 2 3 4 5
●
●
+ 4 - 4
+2 -2 +4 -4
像+2和-2,+4和-4 这样 ,只有符号不同的 两个数 叫做互为相反数。
(特别地,0的相反数是0)
理解新知
像+2和-2,+4和-4 这样 ,只有符号不同的 两个数 叫做互为相反数。
(特别地,0的相反数是0)
思考:
1、“只有”二字可以省略吗?为什么?
2、“相反数”前面的“互为”二字说明什么?
0
1
2
3
-1
-2
-3
在数轴上描出-2,2,-3,3,-1,1这些互为相反数的点,思考这些点在数轴上的位置有什么关系?
二 相反数的几何意义
每组的两个数,在数轴上对应的点都位于原点的两侧,且原点的距离相等
你还能举出其他的例子吗?
1.在数轴上,与原点的距离是2的点有几个?这些点各表示哪些数?
设a是一个正数,数轴上与原点距离是a的点有两个,分别在原点左右,表示-a和a,我们说这两个点关于原点对称。
数轴上表示相反数的两个点分别在原点左右,到原点的距离相等,是关于原点对称的。
2.设a是一个正数,数轴上与原点距离是a的点有几个,这些点表示的数有什么关系?
自主探索
正数的相反数是负数
负数的相反数是正数
零的相反数是0
借助数轴探索,正数,负数,零的相反数分别是什么?
结合数轴考虑:
0的相反数是_____。
一个正数的相反数是一个 。
一个负数的相反数是一个 。
负数
正数
一个数的相反数是它本身的数是______。
0
0
求相反数的方法
1. 在原数的前面加“–”号后,再进行符号化简.
2. 复杂的数在求相反数前,可先进行符号化简,然后再变号.
探究新知
方法总结
如果a = –a,那么表示a的点在数轴上的位置是在( )
A.原点左侧 B.原点右侧
C.原点上或原点右侧 D.原点上
巩固练习
解析:a = –a表示a与它的相反数–a相等,因为只有0的相反数等于它本身.
D
用相反数化简一个数的符号
-(-6)=______; +(-6)=________;
-(+0.73)=_______;-0=________;
-(-34)=________; -(- )=
如何进行符号化简呢?你能自己总结出简化符号的规律吗?
6
-6
-0.73
0
34
归纳
括号外的符号与括号内的符号同号,则化简符号后的数是正数;括号内、外符号异号,则化简符号后的数是负数.
这就是双重符号的化简
1. -[-(-4)]=
2. -[-(+3.5)]=
3. -{-[-(-5)]}=
例 根据以上归纳,解答下列各题.
归纳
多重符号化简的依据:相反数的意义是多重符号化简的依据.-a的实质就是求a的相反数.一般地,-(-a)=a,-(+a)=-a.
多重符号的化简:多重符号化简的结果由“-”号的个数决定,与“+”号无关.如果“-”号个数是奇数,那么结果为负数;如果“-”号个数是偶数,那么结果是正数.
能力拓展
已知数轴上的点A和点B分别表示互为相反数的两个数a,b,且a解:a=-2,b=2
1.-1.6是____的相反数,____的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和 B. 与
C. 与
3.5的相反数是____;a的相反数是___;
4. 的相反数是_____,-3x的相反数是__ _.
1.6
-a
-5
C
-0.3
基础巩固
3x
连接中考
2. 点A在数轴上的位置如图所示,则点A表示的数的相反数是 .
C
–2
1. –8的相反数是( )
A.–8 B. C.8 D.
2. a-3的相反数可以表示为________,
x + y的相反数可以表示为________,
-{-[-(-3)]} =_______.
-(a-3)
-(x+y)
3
综合运用
1.若2x+1是–9的相反数,求x的值.
解:由相反数的意义,得
2x+1=9
2x=8
x=4
-a+3 或a-3
-x-y
3. (1)若 a = 3.2,则 –a = ;
(2)若 –a = 2, 则 a = ;
(3)若-(-a)=3,则 -a= ;
(4)-(a-b)= .
综合运用
-2
-3.2
-3
-a+b
拓展思考:已知两个有理数x、y,且x+y=0, 那么这两个可能有理数有什么关系?
这两个有理数可能互为相反数.
b-a
课堂总结
2.相反数的几何意义:数轴上表示相反数的两个对应点,分别位于原点两侧,它们到原点距离相等。
1.相反数的定义:只有符号不同的两个数叫互为相反数。
3.多重符号的化简:“数负号,奇负偶正”。
Thank you!
人教版
七年级上册
第 1 章 有理数
1.2.1 有理数
人教版· 数学· 七年级(上)
第一章 有理数
第3课时 相反数
1.借助数轴理解相反数的意义,了解数轴上表示相反数的两个点关于原点对称.
2.会求有理数的相反数.
学习目标
在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
数轴上与原点的距离是2的点有两个,分别表示-2和2.
2个单位长度
2个单位长度
导入新知
设a是一个正数,数轴上与原点的距离等于a(a为正数)的点有几个?这些点表示的数有什么关系?
如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右两侧,表示-a和a,我们说这两个点关于原点对称.
在数轴上与原点的距离是2的点有两个,分别表示的数是2和-2.
观察:
+ 2 - 2
只有符号不同
想一想:
在数轴上,距离原点4个单位长度的点所表示的数有几个?这些点各表示哪些数?
-4 -3 -2 -1 0 1 2 3 4 5
●
●
+ 4 - 4
+2 -2 +4 -4
像+2和-2,+4和-4 这样 ,只有符号不同的 两个数 叫做互为相反数。
(特别地,0的相反数是0)
理解新知
像+2和-2,+4和-4 这样 ,只有符号不同的 两个数 叫做互为相反数。
(特别地,0的相反数是0)
思考:
1、“只有”二字可以省略吗?为什么?
2、“相反数”前面的“互为”二字说明什么?
0
1
2
3
-1
-2
-3
在数轴上描出-2,2,-3,3,-1,1这些互为相反数的点,思考这些点在数轴上的位置有什么关系?
二 相反数的几何意义
每组的两个数,在数轴上对应的点都位于原点的两侧,且原点的距离相等
你还能举出其他的例子吗?
1.在数轴上,与原点的距离是2的点有几个?这些点各表示哪些数?
设a是一个正数,数轴上与原点距离是a的点有两个,分别在原点左右,表示-a和a,我们说这两个点关于原点对称。
数轴上表示相反数的两个点分别在原点左右,到原点的距离相等,是关于原点对称的。
2.设a是一个正数,数轴上与原点距离是a的点有几个,这些点表示的数有什么关系?
自主探索
正数的相反数是负数
负数的相反数是正数
零的相反数是0
借助数轴探索,正数,负数,零的相反数分别是什么?
结合数轴考虑:
0的相反数是_____。
一个正数的相反数是一个 。
一个负数的相反数是一个 。
负数
正数
一个数的相反数是它本身的数是______。
0
0
求相反数的方法
1. 在原数的前面加“–”号后,再进行符号化简.
2. 复杂的数在求相反数前,可先进行符号化简,然后再变号.
探究新知
方法总结
如果a = –a,那么表示a的点在数轴上的位置是在( )
A.原点左侧 B.原点右侧
C.原点上或原点右侧 D.原点上
巩固练习
解析:a = –a表示a与它的相反数–a相等,因为只有0的相反数等于它本身.
D
用相反数化简一个数的符号
-(-6)=______; +(-6)=________;
-(+0.73)=_______;-0=________;
-(-34)=________; -(- )=
如何进行符号化简呢?你能自己总结出简化符号的规律吗?
6
-6
-0.73
0
34
归纳
括号外的符号与括号内的符号同号,则化简符号后的数是正数;括号内、外符号异号,则化简符号后的数是负数.
这就是双重符号的化简
1. -[-(-4)]=
2. -[-(+3.5)]=
3. -{-[-(-5)]}=
例 根据以上归纳,解答下列各题.
归纳
多重符号化简的依据:相反数的意义是多重符号化简的依据.-a的实质就是求a的相反数.一般地,-(-a)=a,-(+a)=-a.
多重符号的化简:多重符号化简的结果由“-”号的个数决定,与“+”号无关.如果“-”号个数是奇数,那么结果为负数;如果“-”号个数是偶数,那么结果是正数.
能力拓展
已知数轴上的点A和点B分别表示互为相反数的两个数a,b,且a
1.-1.6是____的相反数,____的相反数是0.3.
2.下列几对数中互为相反数的一对为( ).
A. 和 B. 与
C. 与
3.5的相反数是____;a的相反数是___;
4. 的相反数是_____,-3x的相反数是__ _.
1.6
-a
-5
C
-0.3
基础巩固
3x
连接中考
2. 点A在数轴上的位置如图所示,则点A表示的数的相反数是 .
C
–2
1. –8的相反数是( )
A.–8 B. C.8 D.
2. a-3的相反数可以表示为________,
x + y的相反数可以表示为________,
-{-[-(-3)]} =_______.
-(a-3)
-(x+y)
3
综合运用
1.若2x+1是–9的相反数,求x的值.
解:由相反数的意义,得
2x+1=9
2x=8
x=4
-a+3 或a-3
-x-y
3. (1)若 a = 3.2,则 –a = ;
(2)若 –a = 2, 则 a = ;
(3)若-(-a)=3,则 -a= ;
(4)-(a-b)= .
综合运用
-2
-3.2
-3
-a+b
拓展思考:已知两个有理数x、y,且x+y=0, 那么这两个可能有理数有什么关系?
这两个有理数可能互为相反数.
b-a
课堂总结
2.相反数的几何意义:数轴上表示相反数的两个对应点,分别位于原点两侧,它们到原点距离相等。
1.相反数的定义:只有符号不同的两个数叫互为相反数。
3.多重符号的化简:“数负号,奇负偶正”。
Thank you!
人教版
七年级上册
第 1 章 有理数
