类比与归纳[下学期]

课件13张PPT。类比与归纳思想例1.如图所示,1,3,6,10…称为三角形数(1)求出第n个三角形数tn;
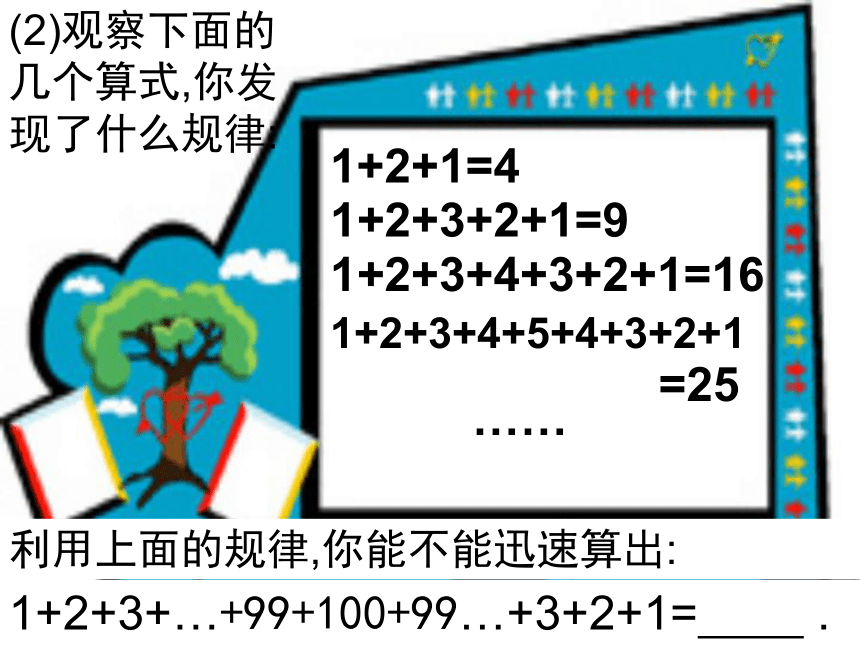
(2)证明8tn+1为完全平方数.(2)观察下面的几个算式,你发现了什么规律:1+2+1=41+2+3+2+1=91+2+3+4+3+2+1=161+2+3+4+5+4+3+2+1 ……利用上面的规律,你能不能迅速算出:1+2+3+…+99+100+99…+3+2+1= .=25(3)观察下列等式:
36-16=20…这些等式反映出自然数间的某种规律,设n表示自然数,试用关于n的等式表示出你所发现的规律: .9-1=8，16-4=12，25-9=16，(4)已知31=3，32=9， 33=27， 34=81，35=343，36=729，37=2187，38=6561,
…推到320的个位数是 .(5)比较下面列算式结果的大小:(在横线上选填”>”、”<”、”=”) 通过观察归纳,写出能反映这种规律的一种结论,并加以证明.数学中的一些基本规律
1+2+3+···+n=n（n+1）/2
1+3+5+···+（2n-1）=n2
2+4+6+···+2n=n（n+1）
12+22+32+···+n2=n（n+1）（2n+1）/6
13+23+33+43+···+n3=n2（n+1）2/4
12+32+52+···+（2n-1）2=n（4n2-1）/3
13+33+53+···+（2n-1）3=n2（2n2-1）例2.(1)判断下列各式是否成立,你认为成立的请在括号内打”√”,不成立的打”χ”① ( )③ ( )② ( )④ ( )(2)你判断完以上各题之后,发现了什么规律?请用含有n的式子将规律表示出来,并注明n的取值范围: .(3)请用数学知识说明你所写式子的正确性.例3.如图,⊙O1和⊙O2外离,BC是两圆的外公切线,切点分别为B、C,连心线O1O2分别交两圆于A、D，BA和CD的延长线交于点E,试判断∠E是什么样的角.例4.有若干个数,第一个数记为a1,第二个数记为a2,第三个数记为a3,……,第n个数记为an.若a1=3,第二个数起,每个数都等于1与它前面那个数的差的倒数.(1)试计算a2,a3,a4;(2)根据以上的计算结果,请你直接写出a2001、a2003各是多少?(3)若a1=k,(2)中a2001、a2003分别又是多少验 (直接写出结论)?例5.计算:(1)1×2×3×4+1=25=52;(2) 2×3×4×5+1=( )2;(3) 3×4×5×6+1=( )2;……(4)根据以上的计算,你能得出一个什么规律(用文字说明)?(5)设第一个数为n,证明你得出的结论.例6.操作:第一次将圆周分成两个半圆,在每个分点标上数3,第二次将两个半圆周的每一个分成两个相等的 圆周,在新产生的分点标上相邻两数和的 ;第三次将四个 圆周的每一个分两个相等的 圆周,在新产生的分点标上其相邻两数和的 ;第四次将八个 圆周的每一个分成两个相等的 圆周,在新产生的分点标上其相邻两数和的 ……如此进行了n次,各次操作的圆上各数的和为An(1)在图所示的各个圆圈中标出数(2)填上A1.A2.A3.A4的值(4)猜想An= .试说明理由 (1)经过⊙O内或⊙O外一点P作两条直线交⊙O于AB和CD四点(图5.6中,有重合的点),得到了如图1-6所表示的六种不同情况.在六种不同情况下,PA.PB.PC.PD四条线段之间在数量上满足的关系式可以用同一个式子表示出来,请你首先写出这个式子,然后只就如图2所示的圆内两条相交弦相交的一般情况,给出证明;(2)已知⊙O的半径为一定值r,若点P不在⊙O上的一个定点,请你过点P任作一直线交⊙O于不重合的两点E.F,PE.PF的值是否为定值?为什么?由此你发现了什么结论?请你把这一结论用文字叙述出来.提高训练CB