直角三角形相似的判定(一)[下学期]
文档属性
| 名称 | 直角三角形相似的判定(一)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-08 18:56:00 | ||
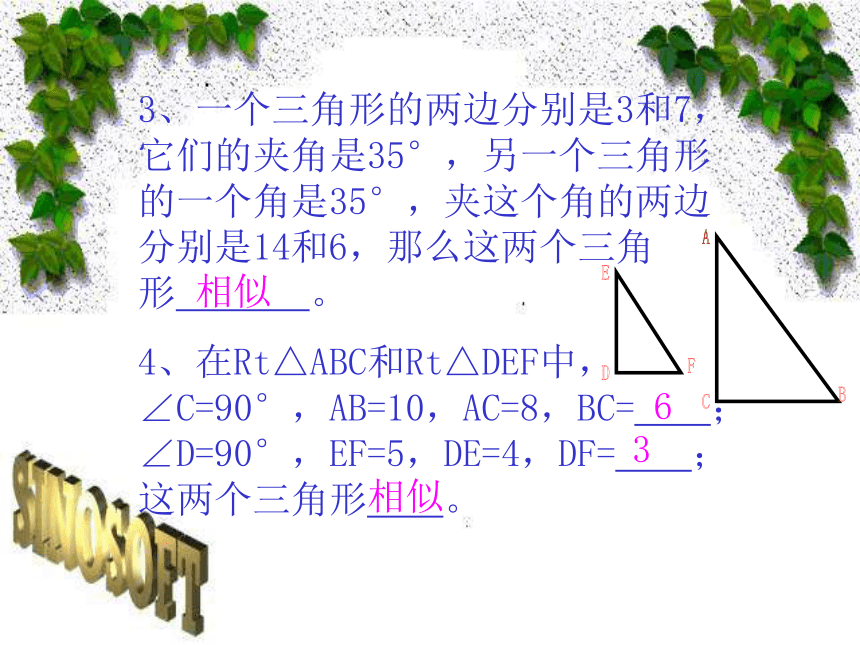
图片预览





文档简介
课件16张PPT。直角三角形相似的判定ABCabcA′B′C′∟一、复习提问1、到目前为止我们总共学过几种判定两 个三
角形相似的方法?答:
(1)两角对应相等的两个三角形相似。
(2)两边对应成比例且夹角相等的两个三角形相似。
(3)三边对应成比例的两个三角形相似。
2、判定两个直角三角形相似有几种方法?答:一个锐角对应相等或两直角边对应成比例。相似相似相似相似63BDEFACA返回上一张下一张已知:如图所示,Rt⊿ABC与Rt⊿A′B′C′中,∠C=∠C′=90°,
求证: Rt⊿ABC∽Rt⊿A′B′C′BCA′B′C′A证明∵ =∴=∴==∴=由勾股定理,得=∵ 和 都是正数。∴ 即==又∠C=∠C′=90° ∴ Rt⊿ABC∽Rt⊿A′B′C′1、∠A=25°,∠B′=65°。AC=3,BC=4,A′C′=6,B′C′=8。3、AB=10,AC=8,A′B′=15, B′C′=9。55°12343a例:如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,⊿ABC∽ ⊿CDB?ABDCab分析:要使R t⊿ABC∽ R t⊿CDB
而题中已经知道R t⊿ABC的斜边和一直角边及R t⊿CDB的斜边,利用今天讲的这个定理可知只须加上条件 = 即可。解:∵ ∠ABC=∠CDB=90°
∴当 = 时, ⊿ABC∽ ⊿CDB。
即当 = 时, ⊿ABC∽ ⊿CDB
∴BD=
答:当BD= 时, ⊿ABC∽ ⊿CDB
问:若改为⊿ABC∽ ⊿BDC,结果如何?
CBD三、小结1、如何判定两个直角三角形相似呢?
答:一个锐角对应相等或两边对应成比例的两个直角三角形相似。
2、直角三角形相似的判定定理的简单应用。3、初步了解转移比例的证法。作业:练习册135-136页1、2、3、4题。
角形相似的方法?答:
(1)两角对应相等的两个三角形相似。
(2)两边对应成比例且夹角相等的两个三角形相似。
(3)三边对应成比例的两个三角形相似。
2、判定两个直角三角形相似有几种方法?答:一个锐角对应相等或两直角边对应成比例。相似相似相似相似63BDEFACA返回上一张下一张已知:如图所示,Rt⊿ABC与Rt⊿A′B′C′中,∠C=∠C′=90°,
求证: Rt⊿ABC∽Rt⊿A′B′C′BCA′B′C′A证明∵ =∴=∴==∴=由勾股定理,得=∵ 和 都是正数。∴ 即==又∠C=∠C′=90° ∴ Rt⊿ABC∽Rt⊿A′B′C′1、∠A=25°,∠B′=65°。AC=3,BC=4,A′C′=6,B′C′=8。3、AB=10,AC=8,A′B′=15, B′C′=9。55°12343a例:如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,⊿ABC∽ ⊿CDB?ABDCab分析:要使R t⊿ABC∽ R t⊿CDB
而题中已经知道R t⊿ABC的斜边和一直角边及R t⊿CDB的斜边,利用今天讲的这个定理可知只须加上条件 = 即可。解:∵ ∠ABC=∠CDB=90°
∴当 = 时, ⊿ABC∽ ⊿CDB。
即当 = 时, ⊿ABC∽ ⊿CDB
∴BD=
答:当BD= 时, ⊿ABC∽ ⊿CDB
问:若改为⊿ABC∽ ⊿BDC,结果如何?
CBD三、小结1、如何判定两个直角三角形相似呢?
答:一个锐角对应相等或两边对应成比例的两个直角三角形相似。
2、直角三角形相似的判定定理的简单应用。3、初步了解转移比例的证法。作业:练习册135-136页1、2、3、4题。
