24.4弧长和扇形面积 课件
文档属性
| 名称 | 24.4弧长和扇形面积 课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 174.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-21 15:43:21 | ||
图片预览




文档简介
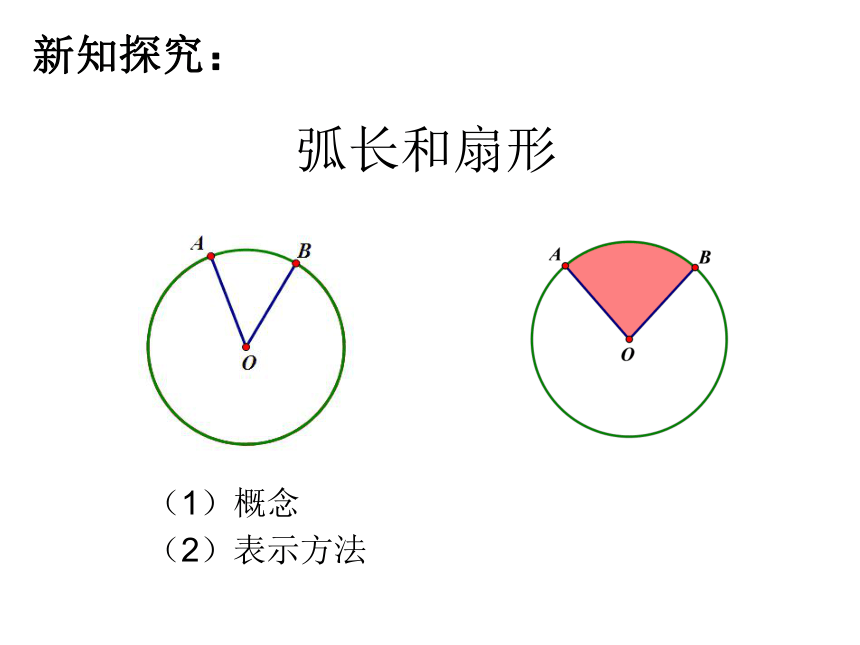
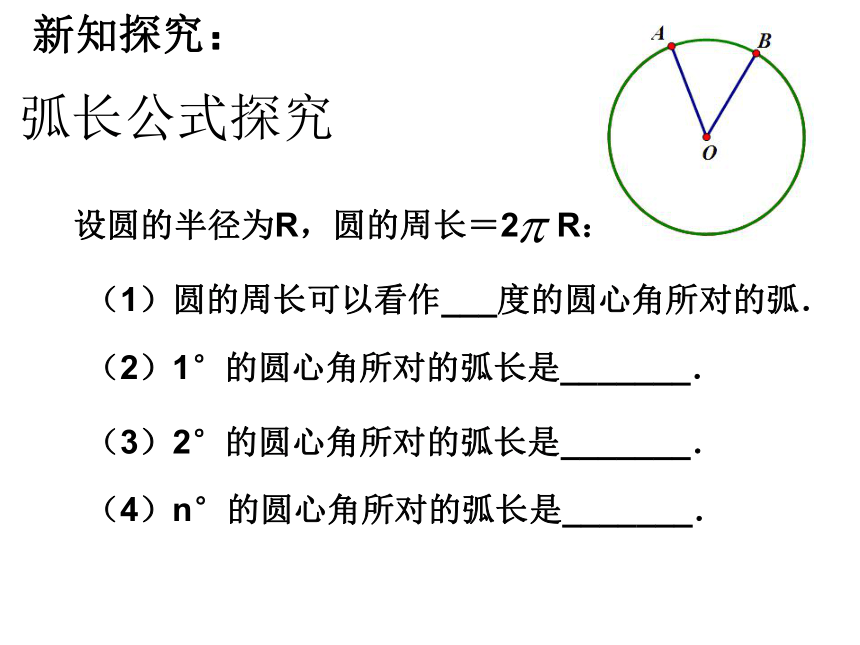
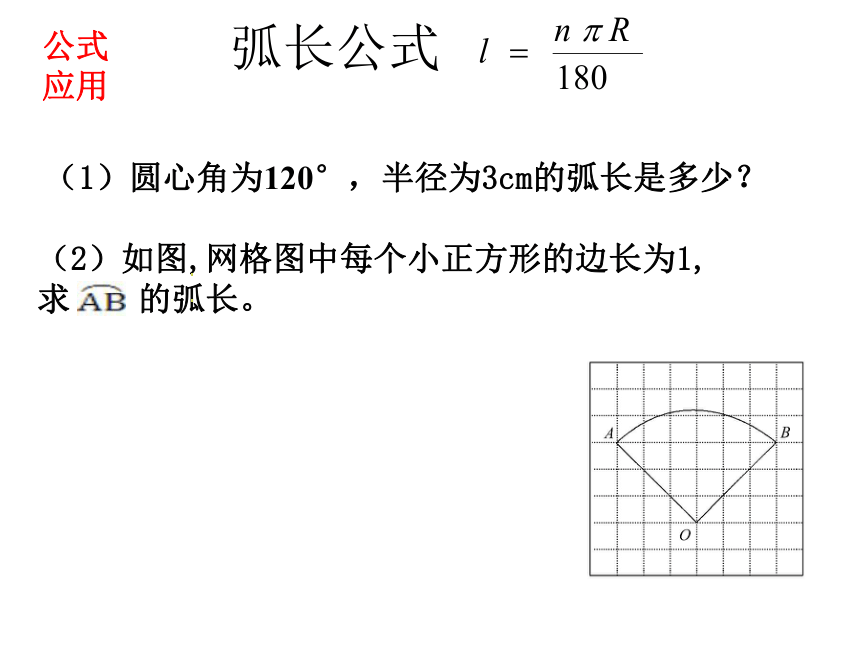
课件17张PPT。制造弯形管道时,要先按中心线计算“展直长度”(虚线的长度),再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)创设情境24.4.1弧长和扇形面积学习目标了解扇形的概念,理解弧长和扇形面积的计算公式,并应用这些公式解决相关问题。新知探究: 弧长和扇形(1)概念(2)表示方法弧长公式探究新知探究: (4)n°的圆心角所对的弧长是_______.设圆的半径为R,圆的周长=2 R:(1)圆的周长可以看作___度的圆心角所对的弧.(2)1°的圆心角所对的弧长是_______.(3)2°的圆心角所对的弧长是_______.弧长的公式弧长公式(1)圆心角为120°,半径为3cm的弧长是多少? (2)如图,网格图中每个小正方形的边长为1,
求 的弧长。公式应用新知探究: 扇形面积公式探究(1)圆的面积可以看作是_______度的圆心角 所对的扇形的面积.(2)1°的圆心角所对的扇形面积S扇形=_______.(3)2°的圆心角所对的扇形面积S扇形=_______.(4)n°的圆心角所对的扇形面积S扇形=_______.(5)60°的圆心角,半径为2cm,S扇形=_______. 观察比较弧长和扇形的公式:
用弧长 表示扇形的面积
S扇形=_______.公式应用 2、求弧长为4 cm,圆心角60°的扇形的面积。 1、求弧长为18cm,半径为3cm的扇形的面积。问题解决:1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长因此所要求的展直长度 2、如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)CD问题解决问题解决3、某花园内有一块四边形的空地如图所示,为了美化环境,现计划在以四边形各顶点为圆心,1m长为半径的扇形区域内(阴影部分)种上花草,那么种上花草的扇形区域总面积是多少? 课堂小结(1)本节课的数学知识:(2)本节课的数学思想和方法有 。 1.弧长公式:2.扇形的面积公式:类比转化课堂检测1.扇形的圆心角为120°,半径为6,则扇形的弧长=
2.扇形的圆心角为60°,半径为6,则扇形的面积=
3.如图,一个圆心角为90°的扇形,半径OA=2.图中阴影部分的面积为 .(结果保留π))拓展与提高 如图CD为☉O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小.
(2)求阴影部分的面积
再见
求 的弧长。公式应用新知探究: 扇形面积公式探究(1)圆的面积可以看作是_______度的圆心角 所对的扇形的面积.(2)1°的圆心角所对的扇形面积S扇形=_______.(3)2°的圆心角所对的扇形面积S扇形=_______.(4)n°的圆心角所对的扇形面积S扇形=_______.(5)60°的圆心角,半径为2cm,S扇形=_______. 观察比较弧长和扇形的公式:
用弧长 表示扇形的面积
S扇形=_______.公式应用 2、求弧长为4 cm,圆心角60°的扇形的面积。 1、求弧长为18cm,半径为3cm的扇形的面积。问题解决:1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长因此所要求的展直长度 2、如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积。(精确到0.01cm)CD问题解决问题解决3、某花园内有一块四边形的空地如图所示,为了美化环境,现计划在以四边形各顶点为圆心,1m长为半径的扇形区域内(阴影部分)种上花草,那么种上花草的扇形区域总面积是多少? 课堂小结(1)本节课的数学知识:(2)本节课的数学思想和方法有 。 1.弧长公式:2.扇形的面积公式:类比转化课堂检测1.扇形的圆心角为120°,半径为6,则扇形的弧长=
2.扇形的圆心角为60°,半径为6,则扇形的面积=
3.如图,一个圆心角为90°的扇形,半径OA=2.图中阴影部分的面积为 .(结果保留π))拓展与提高 如图CD为☉O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小.
(2)求阴影部分的面积
再见
同课章节目录
