北师大版七年级上册数学第一章 丰富的图形世界 练习题(含答案)
文档属性
| 名称 | 北师大版七年级上册数学第一章 丰富的图形世界 练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 176.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 06:45:04 | ||
图片预览


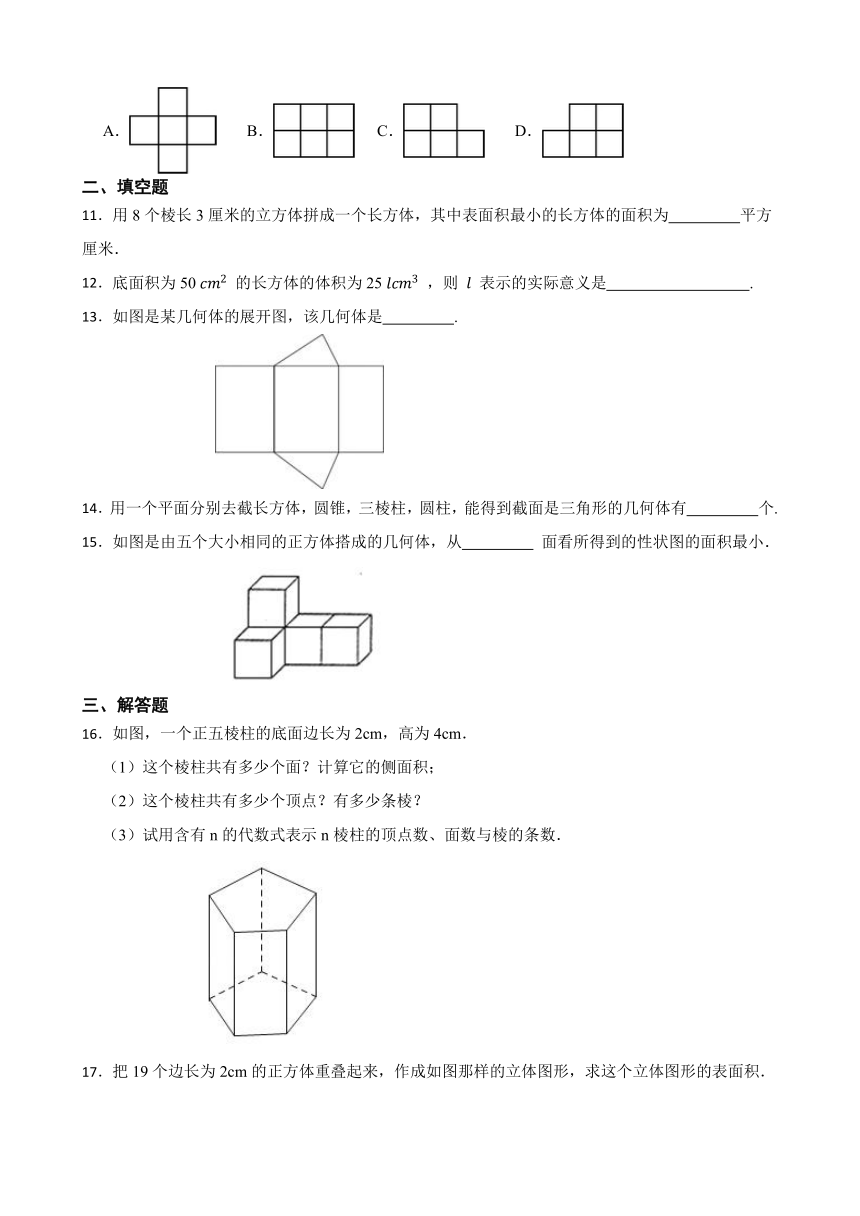
文档简介
北师大版七年级上册数学第一章丰富的图形世界练习题(含答案)
一、单选题
1.下列立体图形的面都是平面的是( )
A.球 B.圆锥 C.圆柱 D.棱柱
2.如图,含有曲面的几何体编号是( )
A.①②③ B.②③④ C.①④⑤ D.②③
3.下列几何体中,面的个数最多的是( )
A. B. C. D.
4.2022年2月7日,中国女足不屈不挠、力闯难关,以骄人战绩时隔16年再次夺得亚洲杯冠军.如图所示,小楠将“中国女足夺冠”这句话写在了一个正方体的表面展开图上,那么在原正方体中,与“冠”所在面相对的面上的汉字是( )
A.中 B.国 C.女 D.足
5.下列图形中,不是正方体的表面展开图的是( )
A. B. C. D.
6.如图,将长方体表面展开,下列选项中错误的是( )
A. B. C. D.
7.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有( )
A.1个 B.2个 C.3个 D.4个
8.用一个平面去截一个正方体,截面形状不能为( )
A. B. C. D.
9.如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是( )
A.图甲的主视图与图乙的左视图形状相同 B.图甲的左视图与图乙的俯视图形状相同
C.图甲的俯视图与图乙的俯视图形状相同 D.图甲的主视图与图乙的主视图形状相同
10.几个大小相同的小正方体搭成几何体的俯视图如图所示,图中小正方形中数字表示对应位置小正方体的个数,该几何体的主视图是( )
A. B. C. D.
二、填空题
11.用8个棱长3厘米的立方体拼成一个长方体,其中表面积最小的长方体的面积为 平方厘米.
12.底面积为50 的长方体的体积为25 ,则 表示的实际意义是 .
13.如图是某几何体的展开图,该几何体是 .
14.用一个平面分别去截长方体,圆锥,三棱柱,圆柱,能得到截面是三角形的几何体有 个.
15.如图是由五个大小相同的正方体搭成的几何体,从 面看所得到的性状图的面积最小.
三、解答题
16.如图,一个正五棱柱的底面边长为2cm,高为4cm.
(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.
17.把19个边长为2cm的正方体重叠起来,作成如图那样的立体图形,求这个立体图形的表面积.
18.请你举出利用圆柱体、长方体的表面能展开成平面图形的原理,在生产和生活中做圆柱形和长方体用品的实例.
19.正方体是由六个平面图形围成的立体图形.设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形.但同一个正方体,按不同的方式展开所得的平面展开图悬不一样的,下面的图形是由6个大小一样的正方彤,拼接而成的,请问这些图形中哪些可以折成正方体
20.如图所示,说出下列几何体截面(阴影部分)的形状.
21.如图是三个三棱柱,用一刀切下去.
(1)把图①中的三棱柱分割成两个完全相同的三棱柱;
(2)把图②中的三棱柱分割成一个四棱锥与一个三棱锥;
(3)把图③中的三棱柱分割成一个四棱柱与一个三棱柱.
22.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
23.某一空间图形的三视图如图,其中主视图:半径为1的半圆以及高为1的矩形;左视图:半径为1的圆以及高为1的矩形;俯视图:半径为1的圆.求此图形的体积.
答案
1.D 2.D 3.C 4.B 5.D 6.C 7.B 8.A 9.B 10.D 11.216
12.长方体高的2倍 13.三棱柱 14.3 15.左
16.解:(1)侧面有5个,底面有2个,共有5+2=7个面;
侧面积:2×5×4=40(cm2).
(2)顶点共10个,棱共有15条;
(3)n棱柱的顶点数2n;面数n+2;棱的条数3n.
17.解:这个立体图形的表面积是4×2×(9+8+10)=216(平方厘米),
答:这个立体图形的表面积是216平方厘米.
18.圆柱体的展开图是由两个相同的圆和一个长方形组成。圆的周长等于长方形的长,确定好长方形的长,就可以计算出圆的直径或半径,就可以运用数据来切割。同时,如果油桶的容积固定,也可以设定一个油桶高度或者油桶底面半径,推算出其他数据。
长方体包装盒在生产和生活中运用较为广泛,因为长方体的展开图,相对的面相同。同时,长方体的大小是由长、宽、高的长度来决定,可以通过设定长方体的容积和长宽高中的任意两个值,推算出第三个值,然后再按照长方体的展开图进行裁剪,裁剪后的图形就可以折叠成所需要的物体。
19.解:(1)、(2)、(3)、(4)、(6)、(10)、(11)、(12)可以折成正方体。
20.三角形截面,等腰三角形截面,长方形截面,圆形截面
解答:(1)切了三个面,可以得到三角形截面;(2)沿圆锥的高线切割,可得到等腰三角形截面;(3)沿正方体的对角线切割,可得到长方形截面;(4)截面与底平行,可以得到圆形截面.
21.解:(1)(2)(3)如图所示:
22.解:(1)根据三视图可得这个几何体是长方体;(2)由三视图知,几何体是一个长方体,长方体的底面是边长为3的正方形,高是4,则这个几何体的表面积是2×(3×3+3×4+3×4)=66(cm2).答:这个几何体的表面积是66cm2.
23.解:根据题意,该图形为圆柱和一个的球的组合体,
球体积应为V球=πr3=π, 圆柱体积V圆柱=πr2h=π,
则图形的体积是:V球+V圆柱=π.
一、单选题
1.下列立体图形的面都是平面的是( )
A.球 B.圆锥 C.圆柱 D.棱柱
2.如图,含有曲面的几何体编号是( )
A.①②③ B.②③④ C.①④⑤ D.②③
3.下列几何体中,面的个数最多的是( )
A. B. C. D.
4.2022年2月7日,中国女足不屈不挠、力闯难关,以骄人战绩时隔16年再次夺得亚洲杯冠军.如图所示,小楠将“中国女足夺冠”这句话写在了一个正方体的表面展开图上,那么在原正方体中,与“冠”所在面相对的面上的汉字是( )
A.中 B.国 C.女 D.足
5.下列图形中,不是正方体的表面展开图的是( )
A. B. C. D.
6.如图,将长方体表面展开,下列选项中错误的是( )
A. B. C. D.
7.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有( )
A.1个 B.2个 C.3个 D.4个
8.用一个平面去截一个正方体,截面形状不能为( )
A. B. C. D.
9.如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是( )
A.图甲的主视图与图乙的左视图形状相同 B.图甲的左视图与图乙的俯视图形状相同
C.图甲的俯视图与图乙的俯视图形状相同 D.图甲的主视图与图乙的主视图形状相同
10.几个大小相同的小正方体搭成几何体的俯视图如图所示,图中小正方形中数字表示对应位置小正方体的个数,该几何体的主视图是( )
A. B. C. D.
二、填空题
11.用8个棱长3厘米的立方体拼成一个长方体,其中表面积最小的长方体的面积为 平方厘米.
12.底面积为50 的长方体的体积为25 ,则 表示的实际意义是 .
13.如图是某几何体的展开图,该几何体是 .
14.用一个平面分别去截长方体,圆锥,三棱柱,圆柱,能得到截面是三角形的几何体有 个.
15.如图是由五个大小相同的正方体搭成的几何体,从 面看所得到的性状图的面积最小.
三、解答题
16.如图,一个正五棱柱的底面边长为2cm,高为4cm.
(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有n的代数式表示n棱柱的顶点数、面数与棱的条数.
17.把19个边长为2cm的正方体重叠起来,作成如图那样的立体图形,求这个立体图形的表面积.
18.请你举出利用圆柱体、长方体的表面能展开成平面图形的原理,在生产和生活中做圆柱形和长方体用品的实例.
19.正方体是由六个平面图形围成的立体图形.设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形.但同一个正方体,按不同的方式展开所得的平面展开图悬不一样的,下面的图形是由6个大小一样的正方彤,拼接而成的,请问这些图形中哪些可以折成正方体
20.如图所示,说出下列几何体截面(阴影部分)的形状.
21.如图是三个三棱柱,用一刀切下去.
(1)把图①中的三棱柱分割成两个完全相同的三棱柱;
(2)把图②中的三棱柱分割成一个四棱锥与一个三棱锥;
(3)把图③中的三棱柱分割成一个四棱柱与一个三棱柱.
22.一个几何体的三个视图如图所示(单位:cm).
(1)写出这个几何体的名称;
(2)若其俯视图为正方形,根据图中数据计算这个几何体的表面积.
23.某一空间图形的三视图如图,其中主视图:半径为1的半圆以及高为1的矩形;左视图:半径为1的圆以及高为1的矩形;俯视图:半径为1的圆.求此图形的体积.
答案
1.D 2.D 3.C 4.B 5.D 6.C 7.B 8.A 9.B 10.D 11.216
12.长方体高的2倍 13.三棱柱 14.3 15.左
16.解:(1)侧面有5个,底面有2个,共有5+2=7个面;
侧面积:2×5×4=40(cm2).
(2)顶点共10个,棱共有15条;
(3)n棱柱的顶点数2n;面数n+2;棱的条数3n.
17.解:这个立体图形的表面积是4×2×(9+8+10)=216(平方厘米),
答:这个立体图形的表面积是216平方厘米.
18.圆柱体的展开图是由两个相同的圆和一个长方形组成。圆的周长等于长方形的长,确定好长方形的长,就可以计算出圆的直径或半径,就可以运用数据来切割。同时,如果油桶的容积固定,也可以设定一个油桶高度或者油桶底面半径,推算出其他数据。
长方体包装盒在生产和生活中运用较为广泛,因为长方体的展开图,相对的面相同。同时,长方体的大小是由长、宽、高的长度来决定,可以通过设定长方体的容积和长宽高中的任意两个值,推算出第三个值,然后再按照长方体的展开图进行裁剪,裁剪后的图形就可以折叠成所需要的物体。
19.解:(1)、(2)、(3)、(4)、(6)、(10)、(11)、(12)可以折成正方体。
20.三角形截面,等腰三角形截面,长方形截面,圆形截面
解答:(1)切了三个面,可以得到三角形截面;(2)沿圆锥的高线切割,可得到等腰三角形截面;(3)沿正方体的对角线切割,可得到长方形截面;(4)截面与底平行,可以得到圆形截面.
21.解:(1)(2)(3)如图所示:
22.解:(1)根据三视图可得这个几何体是长方体;(2)由三视图知,几何体是一个长方体,长方体的底面是边长为3的正方形,高是4,则这个几何体的表面积是2×(3×3+3×4+3×4)=66(cm2).答:这个几何体的表面积是66cm2.
23.解:根据题意,该图形为圆柱和一个的球的组合体,
球体积应为V球=πr3=π, 圆柱体积V圆柱=πr2h=π,
则图形的体积是:V球+V圆柱=π.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
