切线[下学期]

课件11张PPT。切线的判定 班级：初三年（7）班
授课人：厦门市城东中学 纪文滨
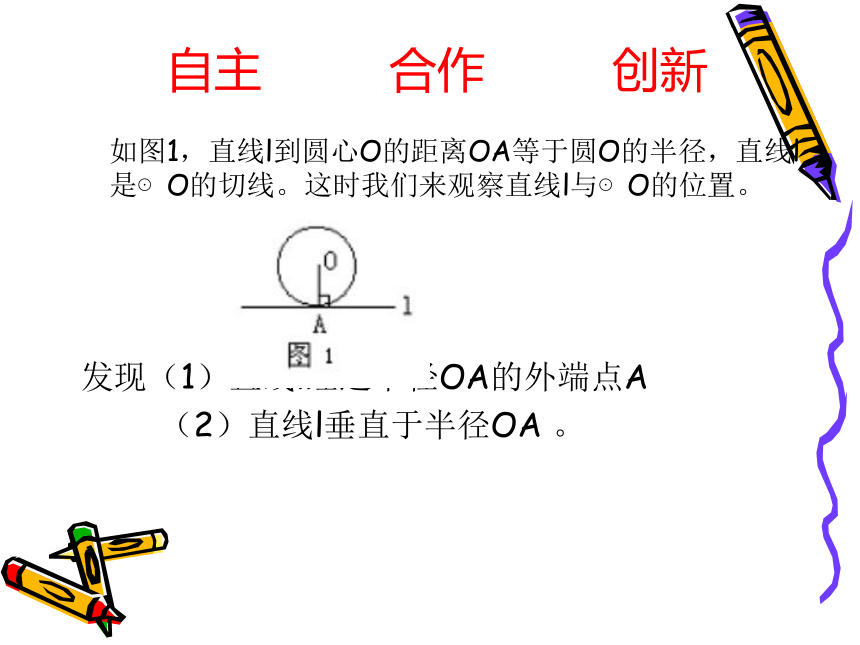
如图1，直线l到圆心O的距离OA等于圆O的半径，直线l是⊙O的切线。这时我们来观察直线l与⊙O的位置。 发现（1）直线l经过半径OA的外端点A
（2）直线l垂直于半径OA 。
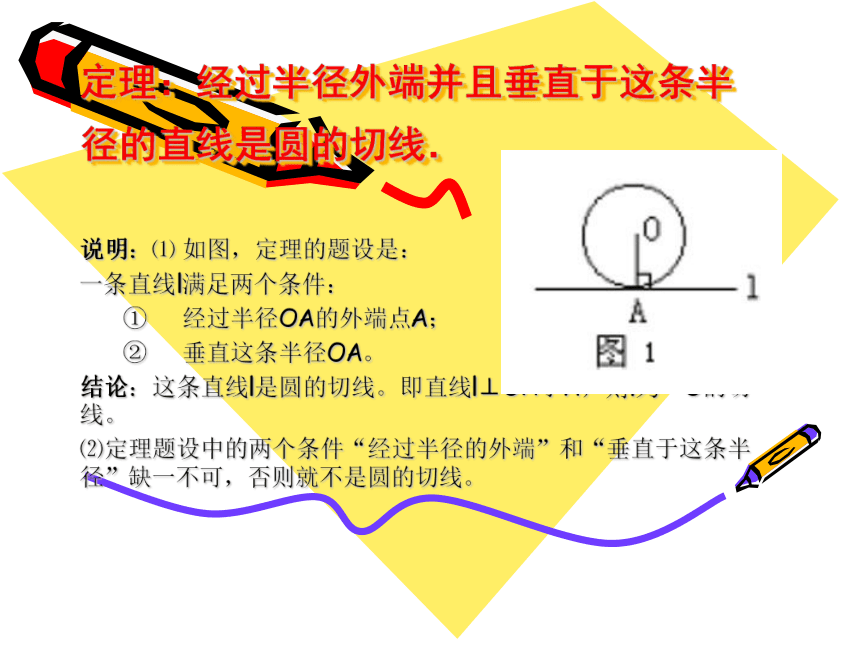
自主 合作 创新定理：经过半径外端并且垂直于这条半径的直线是圆的切线． 说明：⑴ 如图，定理的题设是：
一条直线l满足两个条件：
①???? 经过半径OA的外端点A；
②???? 垂直这条半径OA。
结论：这条直线l是圆的切线。即直线l⊥OA于A，则l为⊙O的切线。
⑵定理题设中的两个条件“经过半径的外端”和“垂直于这条半径”缺一不可，否则就不是圆的切线。
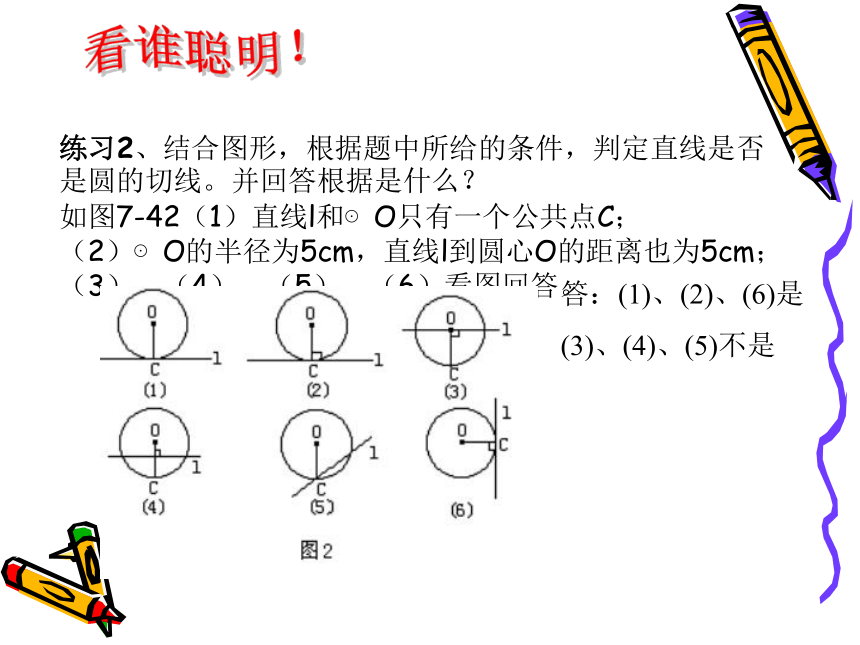
比 谁 快练习1：是非题：（1）垂直于圆的半径的直线一定是这个圆的切线。 （ ）（2）过圆的半径的外端的直线一定是这个圆的切线。 （ ）练习2、结合图形，根据题中所给的条件，判定直线是否是圆的切线。并回答根据是什么？如图7-42（1）直线l和⊙O只有一个公共点C；（2）⊙O的半径为5cm，直线l到圆心O的距离也为5cm；（3）、（4）、（5）、（6）看图回答。看谁聪明！答：(1)、(2)、(6)是
(3)、(4)、(5)不是4、例题：
例1、已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB（如图3）试说明直线AB是⊙O的切线。
证明：连结OC. ∵OA=OB，CA=CB， ∴OC是等腰三角形OAB底边AB上的中线. ∴AB⊥OC 即直线AB经过半径OC的外端C，并且垂直于半径OC， ∴AB是⊙O的切线。 练习3、如图4，AB是⊙O的直径，∠ABC=45°，AC=AB，AC是⊙O的切线吗？为什么？ 比比谁棒！图5练习4、如图5，线段AB经过圆心O，交⊙O于点A、C，∠BAD=∠B = 30°，边BD交圆于点D。BD是⊙O的切线吗？为什么？
机动练习：已知，如图6，△ABC为等腰三角形，O是底边BC的中点，⊙O与腰AB相切于点D。AC与⊙O相切吗？为什么?
总结、扩展
1．切线的判定定理。
2．判定一条直线是圆的切线，我们有哪些方法呢？
①定义：直线和圆有唯一公共点。
②数量关系：直线到圆心的距离等于该圆半径（即d = r）。
③切线的判定定理：经过半径外端且与这条半径垂直的直线是圆的切线。
3．证明一条直线是圆的切线的辅助线和证法规律。 作业
1、如图7，已知△ABC内接于⊙O，P是CB延长线上的一点，连结AP，且AP2 = PB·PC，试说明PA是⊙O的切线。
2、思考题：如图，A是⊙O直径上的一点，OB是和这条直径垂直的半径，BA和⊙O相交于另一点C，过点C的切线和OA的延长线相交于点D，那么DA = DC吗？为什么？
变题1：若将直线DA向上平行移至OB上，DA还会等于DC吗？为什么？
变题2：若将直线DA向上平行移至OB外，DA还会等于DC吗？为什么？