函数应用题解析[下学期]
图片预览


文档简介
课题: 函数应用题解析 班级: 三(5)(10) 授课时间:20 年 月 日
教学目标 通过复习学生能掌握解函数应用题来解题的一般方法和步骤
教学重点 函数应用题的审题和分析问题能力
教学难点 函数应用题的审题和分析问题能力。
教学工具 多媒体进行教学 教学方法 分层次教学
教学流程
一、解答函数应用题的基本步骤:
1.仔细审题,分析问题中常量,变量以及它们之间的关系,找出与两个变量相
关的等量关系;
2.列出函数关系式并化简,如需要写出自变量的取值范围,画出函数的图象;
3.运用函数的知识及相关性质,求得符合实际的答案,并完整地写出答句。
以上步骤中,将实际问题转化为函数关系式,是解决函数应用题的关键。这
个转化过程变就是建立函数模型。建立函数模型的过程和思想方法,类似于建立
方程模型应用题。
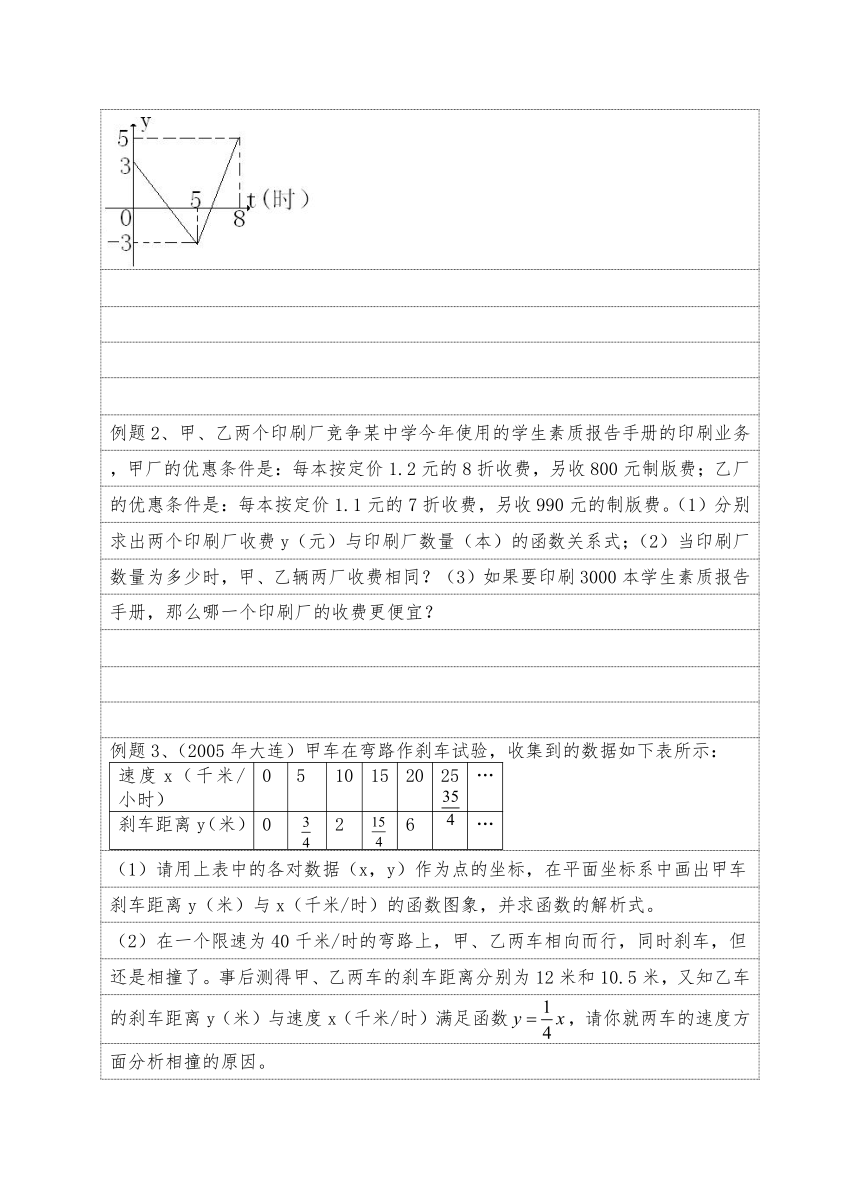
例题1、春、秋季节,由于冷空气的入侵,地面气温急剧下降到00C以下的天气
称为“霜冻”,由霜冻导致植物受到影响或破坏的现象称为霜冻灾害。某种植物
在气温00C以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施。图1
是气象台某天发布的气象信息,预报了次日0时到8时气温随时间变化的情况,
其中0时到5时,5时到8时的图象分别满足一次函数关系。请你根据图中信息
针对这种植物,判断次日是否需要采取措施,并说明理由。
例题2、甲、乙两个印刷厂竞争某中学今年使用的学生素质报告手册的印刷业务
,甲厂的优惠条件是:每本按定价1.2元的8折收费,另收800元制版费;乙厂
的优惠条件是:每本按定价1.1元的7折收费,另收990元的制版费。(1)分别
求出两个印刷厂收费y(元)与印刷厂数量(本)的函数关系式;(2)当印刷厂
数量为多少时,甲、乙辆两厂收费相同?(3)如果要印刷3000本学生素质报告
手册,那么哪一个印刷厂的收费更便宜?
例题3、(2005年大连)甲车在弯路作刹车试验,收集到的数据如下表所示:速度x(千米/小时)0510152025…刹车距离y(米)026…
(1)请用上表中的各对数据(x,y)作为点的坐标,在平面坐标系中画出甲车
刹车距离y(米)与x(千米/时)的函数图象,并求函数的解析式。
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向而行,同时刹车,但
还是相撞了。事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车
的刹车距离y(米)与速度x(千米/时)满足函数,请你就两车的速度方
面分析相撞的原因。
例题4、某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷
的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册)500080001000015000……成本y(元)28500360004100053500……
经过对上表中数据的探究,发现这种读物的投入成本y(元)是印数x(册)
的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入成本48000元,那么能印该读物多少册?
学生练习:见书本P98,教师讲解分析练习
课堂小结:
以现实生活问题为背景的函数应用性问题,成为近年来中考试题的一个亮点,这
类问题取材新,立意巧,有利于考生应用能力的考查。要求学生要理解每个数据
的含义,这是能顺利解决此类问题的关键。同学们在解题时应能迅速找到问题的
关键,将实际问题转化为数学问题,并探求问题中的函数关系式,灵活运用函数
的性质解题。
板书设计 函数应用例题1、 例题2、 例题3、 例题4、
教学反思
课题: 开放性试题 班级: 三(5)(10) 授课时间:20 年 月 日
教学目标 学生能学会对答案不唯一问题的讨论,能够较全面地思考问题,使结论尽可能完整;学生能学会运用观察、想象、分析、归纳、类比、演绎等思维方法,从多个角度思考与探索,获得多种结论,并加以推理论证;培养学生综合分析问题的能力,提高解题的灵活性和完备性;
教学重点 开放性问题的审题是重点
教学难点 结论或条件的多样性分析是本节课的难点
教学工具 多媒体进行教学 教学方法 分层次教学
教学流程
一、开放题的类型一般可分为:
1.条件开放型:即问题的条件不完备或满足结论的条件不唯一;
2.结论开放型:即在给定的条件下,结论不唯一;
3.策略开放型:即思维策略与解题方法不唯一;
4.综合型:即条件、结论、策略中至少有两项均是开放的;
二、各类别型解题要求:
条件开放型就是要求解题者直接写满足结论的有限个条件,或者根据结论论
证应该具备哪些条件;结论开放型就是要求答题者直接写出符合条件的有限个结
论,或者根据条件论证出多个结论;策略开放型就是要求答题者从不同角度探索
问题,或用不同知识点,或用不同解题路径与方法解决同一个问题。
三、例题讲解:
A、条件开放型试题
1.请你写出两个你喜欢的无理数,使它们的和等于有理数______。
2.如图, E、F是□ABCD对角线BD上的两点,请你添加一个适当的条件:
___________ ,使四边形AECF是平行四边形.
B、结论开放型试题
3.写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式 ;
4.已知:如图DC∥AB,且DC=1/2AB,E为AB的中点。(1)求证:ΔAED≌ΔEBC。
(2)观察图形,在不添加辅助线的的情况下,除ΔEBC外,再写出两个与ΔAED
面积相等的三角形: 。(直接写出结果,不要求证明)
C、策略开放型试题
5.要在河的两岸A、B建一座观赏桥,由于条件限制,无法直接测量A、B两点
间的距离。请你用学过的知识,按以下要求设计一种测量方案。(1)画出测量图
案:(1)画出测量图案;(2)写出测量步骤(测量数据用字母表示);(3)计算
AB的距离(写出求解或推测过程,结果用字母表示)。
学生练习:
1.写出一个系数是2005,且含有x、y两个字母的三次单项式: ;
2.先化简代数式,然后选取一个使原式有意义的a值
代入求值.
3.若函数的图象经过点(1,2),则函数的表达式可能是 (写
出一个即可).
4.写出一个函数解析式,使它的图象与X轴的夹角等于450,这个一次函数的解
析式是 ;
5.如果方程X2-m=0有整数根,那么M的值可以是 (只写一个)
6.写出一个含有字母的分式(要求:不论取任何实数,该分式都有意义,且
分式的值为负) .
7.请写出你熟悉的两个无理数__________.
8.在四边形ABCD中,已知AB//CD,请补充条件 (写一个即可),
使得四边形ABCD为平行四边形;若ABCD是平行四边形,请补充条件
(写一个即可),使四边形ABCD为菱形。
9.在△ABC和△ADC中,下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC
将其中的两个论断作为条件,另一个论断作为结论写出一个真命题是 。
10.如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.(1)请你再添加
一个条件,使得△BEA≌△BDC,并给出证明.你添加的条件是: .证明:(2)
根据你添加的条件,再写出图中的一对全等三角形: . (只要求写出一对全
等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)
四、课堂小结:开放型试题是相对常规性问题而言,其条件、结论及其解题目思
路是丰富多彩的,需要学生通过观察、比较、分析、综合甚至猜想,展开发散性
思维,运用已学过的知识和数学方法,经过必要的推理,才能得出正确的结论。
板书设计 开放题复习例题板书1、 2、 3、 学生练习
教学反思
教学目标 通过复习学生能掌握解函数应用题来解题的一般方法和步骤
教学重点 函数应用题的审题和分析问题能力
教学难点 函数应用题的审题和分析问题能力。
教学工具 多媒体进行教学 教学方法 分层次教学
教学流程
一、解答函数应用题的基本步骤:
1.仔细审题,分析问题中常量,变量以及它们之间的关系,找出与两个变量相
关的等量关系;
2.列出函数关系式并化简,如需要写出自变量的取值范围,画出函数的图象;
3.运用函数的知识及相关性质,求得符合实际的答案,并完整地写出答句。
以上步骤中,将实际问题转化为函数关系式,是解决函数应用题的关键。这
个转化过程变就是建立函数模型。建立函数模型的过程和思想方法,类似于建立
方程模型应用题。
例题1、春、秋季节,由于冷空气的入侵,地面气温急剧下降到00C以下的天气
称为“霜冻”,由霜冻导致植物受到影响或破坏的现象称为霜冻灾害。某种植物
在气温00C以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施。图1
是气象台某天发布的气象信息,预报了次日0时到8时气温随时间变化的情况,
其中0时到5时,5时到8时的图象分别满足一次函数关系。请你根据图中信息
针对这种植物,判断次日是否需要采取措施,并说明理由。
例题2、甲、乙两个印刷厂竞争某中学今年使用的学生素质报告手册的印刷业务
,甲厂的优惠条件是:每本按定价1.2元的8折收费,另收800元制版费;乙厂
的优惠条件是:每本按定价1.1元的7折收费,另收990元的制版费。(1)分别
求出两个印刷厂收费y(元)与印刷厂数量(本)的函数关系式;(2)当印刷厂
数量为多少时,甲、乙辆两厂收费相同?(3)如果要印刷3000本学生素质报告
手册,那么哪一个印刷厂的收费更便宜?
例题3、(2005年大连)甲车在弯路作刹车试验,收集到的数据如下表所示:速度x(千米/小时)0510152025…刹车距离y(米)026…
(1)请用上表中的各对数据(x,y)作为点的坐标,在平面坐标系中画出甲车
刹车距离y(米)与x(千米/时)的函数图象,并求函数的解析式。
(2)在一个限速为40千米/时的弯路上,甲、乙两车相向而行,同时刹车,但
还是相撞了。事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车
的刹车距离y(米)与速度x(千米/时)满足函数,请你就两车的速度方
面分析相撞的原因。
例题4、某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷
的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册)500080001000015000……成本y(元)28500360004100053500……
经过对上表中数据的探究,发现这种读物的投入成本y(元)是印数x(册)
的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入成本48000元,那么能印该读物多少册?
学生练习:见书本P98,教师讲解分析练习
课堂小结:
以现实生活问题为背景的函数应用性问题,成为近年来中考试题的一个亮点,这
类问题取材新,立意巧,有利于考生应用能力的考查。要求学生要理解每个数据
的含义,这是能顺利解决此类问题的关键。同学们在解题时应能迅速找到问题的
关键,将实际问题转化为数学问题,并探求问题中的函数关系式,灵活运用函数
的性质解题。
板书设计 函数应用例题1、 例题2、 例题3、 例题4、
教学反思
课题: 开放性试题 班级: 三(5)(10) 授课时间:20 年 月 日
教学目标 学生能学会对答案不唯一问题的讨论,能够较全面地思考问题,使结论尽可能完整;学生能学会运用观察、想象、分析、归纳、类比、演绎等思维方法,从多个角度思考与探索,获得多种结论,并加以推理论证;培养学生综合分析问题的能力,提高解题的灵活性和完备性;
教学重点 开放性问题的审题是重点
教学难点 结论或条件的多样性分析是本节课的难点
教学工具 多媒体进行教学 教学方法 分层次教学
教学流程
一、开放题的类型一般可分为:
1.条件开放型:即问题的条件不完备或满足结论的条件不唯一;
2.结论开放型:即在给定的条件下,结论不唯一;
3.策略开放型:即思维策略与解题方法不唯一;
4.综合型:即条件、结论、策略中至少有两项均是开放的;
二、各类别型解题要求:
条件开放型就是要求解题者直接写满足结论的有限个条件,或者根据结论论
证应该具备哪些条件;结论开放型就是要求答题者直接写出符合条件的有限个结
论,或者根据条件论证出多个结论;策略开放型就是要求答题者从不同角度探索
问题,或用不同知识点,或用不同解题路径与方法解决同一个问题。
三、例题讲解:
A、条件开放型试题
1.请你写出两个你喜欢的无理数,使它们的和等于有理数______。
2.如图, E、F是□ABCD对角线BD上的两点,请你添加一个适当的条件:
___________ ,使四边形AECF是平行四边形.
B、结论开放型试题
3.写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式 ;
4.已知:如图DC∥AB,且DC=1/2AB,E为AB的中点。(1)求证:ΔAED≌ΔEBC。
(2)观察图形,在不添加辅助线的的情况下,除ΔEBC外,再写出两个与ΔAED
面积相等的三角形: 。(直接写出结果,不要求证明)
C、策略开放型试题
5.要在河的两岸A、B建一座观赏桥,由于条件限制,无法直接测量A、B两点
间的距离。请你用学过的知识,按以下要求设计一种测量方案。(1)画出测量图
案:(1)画出测量图案;(2)写出测量步骤(测量数据用字母表示);(3)计算
AB的距离(写出求解或推测过程,结果用字母表示)。
学生练习:
1.写出一个系数是2005,且含有x、y两个字母的三次单项式: ;
2.先化简代数式,然后选取一个使原式有意义的a值
代入求值.
3.若函数的图象经过点(1,2),则函数的表达式可能是 (写
出一个即可).
4.写出一个函数解析式,使它的图象与X轴的夹角等于450,这个一次函数的解
析式是 ;
5.如果方程X2-m=0有整数根,那么M的值可以是 (只写一个)
6.写出一个含有字母的分式(要求:不论取任何实数,该分式都有意义,且
分式的值为负) .
7.请写出你熟悉的两个无理数__________.
8.在四边形ABCD中,已知AB//CD,请补充条件 (写一个即可),
使得四边形ABCD为平行四边形;若ABCD是平行四边形,请补充条件
(写一个即可),使四边形ABCD为菱形。
9.在△ABC和△ADC中,下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC
将其中的两个论断作为条件,另一个论断作为结论写出一个真命题是 。
10.如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.(1)请你再添加
一个条件,使得△BEA≌△BDC,并给出证明.你添加的条件是: .证明:(2)
根据你添加的条件,再写出图中的一对全等三角形: . (只要求写出一对全
等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)
四、课堂小结:开放型试题是相对常规性问题而言,其条件、结论及其解题目思
路是丰富多彩的,需要学生通过观察、比较、分析、综合甚至猜想,展开发散性
思维,运用已学过的知识和数学方法,经过必要的推理,才能得出正确的结论。
板书设计 开放题复习例题板书1、 2、 3、 学生练习
教学反思
同课章节目录
