人教版高中数学必修第一册3.2 函数的基本性质 课时6 函数的最大(小)值 课件(共25张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册3.2 函数的基本性质 课时6 函数的最大(小)值 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1005.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
3.2 函数的基本性质
课时6 函数的最大(小)值
教学目标
1. 理解函数的最大(小)值的概念及其几何意义,了解函数的最值与单调性之间的关系.
2. 能够正确地运用函数的图象和函数的单调性求一些简单函数的最大(小)值与值域.
3. 了解函数图象与性质之间的内在联系,体会函数图象在研究函数问题中的应用功能.
学习目标
课程目标 学科核心素养
借助函数图象,会用符号语言表达函数的最大(小)值,理解函数的最大(小)值的意义 在用符号语言表达函数的最大(小)值的过程中,培养数学抽象与直观想象素养
会求一些简单函数的最大(小)值,进而运用函数的最大(小)值解决实际应用问题 在求解函数的值域、最值以及实际问题的过程中,培养逻辑推理、数学运算等素养
了解函数图象与性质之间的内在联系,体会函数图象在解决函数问题中的作用 在解决问题的过程中,体会函数图象与性质的内在联系,培养数学抽象、数学运算等素养
情境导学
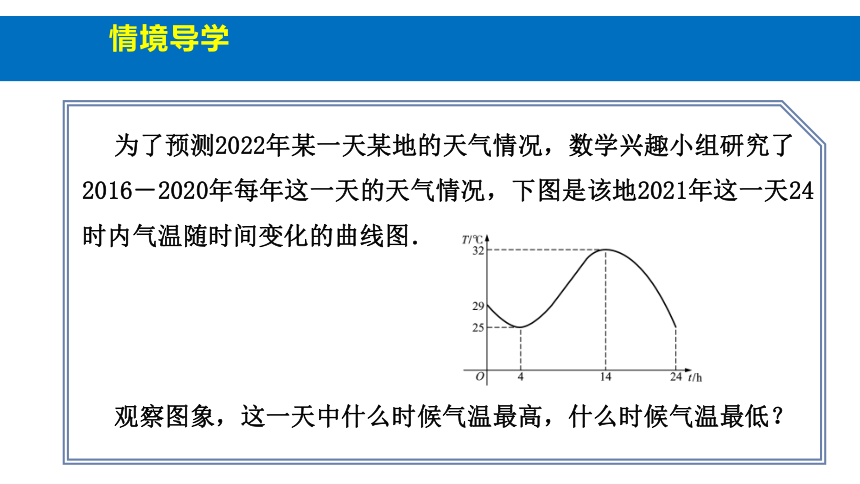
为了预测2022年某一天某地的天气情况,数学兴趣小组研究了2016-2020年每年这一天的天气情况,下图是该地2021年这一天24时内气温随时间变化的曲线图.
观察图象,这一天中什么时候气温最高,什么时候气温最低?
【活动1】 概括函数最大值的含义
初探新知
【问题2】函数最值定义中的条件(2)能不能去掉?为什么?
【问题1】什么是函数的最大值 从函数的图象上如何获得函数的最大值?
【问题3】你能仿照函数最大值的定义,给出函数最小值的定义吗?
【活动2】由函数最大值的含义类比函数最小值的含义
【问题4】你能说出函数的最值和值域的联系与区别吗?
【问题5】若函数y=f(x)在区间 上单调递增,那么函数y=f(x)在区间 上有何最值?
【活动3】探究最大(小)值与单调性的关系
【问题6】若函数y=f(x)在区间 上x=b两侧单调性相反,那么函数y=f(x)在区间 上有何最值?
典例精析
【例1】[教材改编题]函数y=f(x)在[-2,2]上的图象如图,则此函数的最小值、最大值分别是 ( )
A. -1,0 B. 0,2
C. -1,2 D. ,2
【解】由函数的图象可知f(x)的最大值为f(1)=2,f(x)的最小值为f(-2)=-1.故选C.
C
【方法规律】
从函数的图象上来看,函数的最大值就是函数图象的最高点的纵坐标,函数的最小值就是函数图象的最低点的纵坐标,因此,要求函数的最大值与最小值,只要作出函数的图象,求出图象的最高点与最低点的纵坐标即可.
【变式训练1】已知x∈R,定义函数f(x)是y=2-x2,y=x这两个函数中的较小者,则f(x)的最大值为 ( )
A. 2 B. 1
C. -1 D. 无最大值
【解】在同一平面直角坐标系中画出函数y=2-x2,y=x的图象,如图.根据题意,图中实线部分即为函数f(x)的图象.所以当x=1时,f(x)max=1.故选B.
B
【例2】函数y= ,的最大值为________.
思路点拨:求分段函数的最大值,需要先求出每一段在各自范围上的最大值,再比较.注意每段上最大值的求解,需要先判断各段的单调性.也可以通过作出图象来求.
【解】
方法1:当x<1时,函数y=x+3单调递增,且有y<4,无最大值;当x≥1时,函数y=-x+6单调递减,则在x=1处取得最大值,最大值为5.故函数在整个定义域内的最大值为5.
方法2:作出分段函数y= 的图象,如图,由图象可得函数在整个定义域内的最大值为5.
【方法规律】
分段函数的最大(小)值是各段函数最大(小)值中的最大(小)者,或者作出其图象,由图象得出其最大(小)值.
【变式训练2】 求函数y=|x+1|-|x-2|的最大值和最小值.
【解】y=|x+1|-|x-2|=作出函数的图象(图略),由图可知,y∈[-3,3].所以函数的最大值为3,最小值为-3.
【例3】[2021·广东省广州市增城区高一期末改编题] 已知函数f(x)=x2+2ax+1在区间[-1,2]上的最大值为4,求a的值.
思路点拨 求解与二次函数的最大值、最小值有关的问题,应先考虑该函数的定义域,可以采用配方法和图象法求解.
【解】 f(x)=x2+2ax+1=(x+a)2+1-a2,对称轴为直线x=-a,结合二次函数的图象知:当-a≥,即a≤-时,f(x)max=f(-1)=1-2a+1=4,所以a=-1,满足条件;当-a<,即a>-时,f(x)max=f(2)=4+4a+1=4,所以a=-,满足条件.综上所述,a=-1或a=-.
【方法规律】
求解二次函数的最大(小)值,需要综合考虑开口方向和对称轴与定义域区间的位置关系,当二次函数中含有参数时,需根据参数的不同取值进行分类讨论.
【变式训练3】已知函数f(x)=x2-2ax+2,x∈ ,求函数f(x)的最小值.
【解】 f(x)=(x-a)2+2-a2,x∈ .当a≥1时,f(x)在 上单调递减,f(x)min=f(1)=3-2a;当-1(备选例题)已知函数f(x)=,其中a≤1.
(1) 当a=,x∈[1,2]时,求函数f(x)的值域;
(2) 若对任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
思路点拨(1) 当a=,x∈[1,2]时,f(x)=x++2,是单调递增函数,求出其最大值和最小值,即可得到其值域. (2) 分离参数,将不等式恒成立问题转化为求函数的最值问题来处理.
【解】(1) 当a=,x∈[1,2]时,f(x)=x++2,f(x)在x∈[1,2]上是单调递增,证明如下:设1≤x10,2x1x2-1>0,所以f(x1)-f(x2)<0,即f(x1)(2) 当x∈[1,+∞)时,>0恒成立,则x2+2x+a>0对x∈[1,+∞)恒成立,即a>-(x2+2x)在x∈[1,+∞)上恒成立.令g(x)=-(x2+2x)=-(x+1)2+1,x∈[1,+∞),所以g(x)在[1,+∞)上是单调递减,g(x)max=g(1)=-3.又a≤1,所以-3【方法规律】
(1) 若函数f(x)在[a,b]上是单调递增,则f(x)min=f(a),f(x)max=f(b),得值域为[f(a),f(b)],若函数f(x)在[a,b]上是减函数,则f(x)min=f(b),f(x)max=f(a),得值域为[f(b),f(a)].
(2) 不等式恒成立问题常可转化为函数的最值问题借助单调性来求解.
课堂反思
通过本节课的学习,你学到了哪些知识?
2.你认为本节课的重点和难点是什么?
随堂演练
1. [教材改编题]函数f(x)= 的最大值是( )
A. B. C. D.
A
2. [2021·湖南省怀化市高一期末]下列函数中,在(0,+∞)上存在最小值的是( )
A. y=(x-1)2 B. y=
C. y=-x2+2x D. y=2x+1
A
3. (多选)[2021·江苏省常州市高一期末]已知函数f(x)= (x∈[3,5]),下列结论中正确的是( )
A. f(x)是增函数 B. f(x)是减函数
C. f(x)的最大值是 D. f(x)的值域是
ACD
4. 已知函数f(x)=其中m>0,若f(x)的最小值为0,则实数m的取值范围是 .
5. [2021·陕西省汉中市汉台中学高三月考]二次函数f(x)=x2-2x+3在[0,m]上有最大值3,最小值1,则实数m的取值范围是 .
[2,4]
(0,4]
同学们再见!
Goodbye Students!
3.2 函数的基本性质
课时6 函数的最大(小)值
教学目标
1. 理解函数的最大(小)值的概念及其几何意义,了解函数的最值与单调性之间的关系.
2. 能够正确地运用函数的图象和函数的单调性求一些简单函数的最大(小)值与值域.
3. 了解函数图象与性质之间的内在联系,体会函数图象在研究函数问题中的应用功能.
学习目标
课程目标 学科核心素养
借助函数图象,会用符号语言表达函数的最大(小)值,理解函数的最大(小)值的意义 在用符号语言表达函数的最大(小)值的过程中,培养数学抽象与直观想象素养
会求一些简单函数的最大(小)值,进而运用函数的最大(小)值解决实际应用问题 在求解函数的值域、最值以及实际问题的过程中,培养逻辑推理、数学运算等素养
了解函数图象与性质之间的内在联系,体会函数图象在解决函数问题中的作用 在解决问题的过程中,体会函数图象与性质的内在联系,培养数学抽象、数学运算等素养
情境导学
为了预测2022年某一天某地的天气情况,数学兴趣小组研究了2016-2020年每年这一天的天气情况,下图是该地2021年这一天24时内气温随时间变化的曲线图.
观察图象,这一天中什么时候气温最高,什么时候气温最低?
【活动1】 概括函数最大值的含义
初探新知
【问题2】函数最值定义中的条件(2)能不能去掉?为什么?
【问题1】什么是函数的最大值 从函数的图象上如何获得函数的最大值?
【问题3】你能仿照函数最大值的定义,给出函数最小值的定义吗?
【活动2】由函数最大值的含义类比函数最小值的含义
【问题4】你能说出函数的最值和值域的联系与区别吗?
【问题5】若函数y=f(x)在区间 上单调递增,那么函数y=f(x)在区间 上有何最值?
【活动3】探究最大(小)值与单调性的关系
【问题6】若函数y=f(x)在区间 上x=b两侧单调性相反,那么函数y=f(x)在区间 上有何最值?
典例精析
【例1】[教材改编题]函数y=f(x)在[-2,2]上的图象如图,则此函数的最小值、最大值分别是 ( )
A. -1,0 B. 0,2
C. -1,2 D. ,2
【解】由函数的图象可知f(x)的最大值为f(1)=2,f(x)的最小值为f(-2)=-1.故选C.
C
【方法规律】
从函数的图象上来看,函数的最大值就是函数图象的最高点的纵坐标,函数的最小值就是函数图象的最低点的纵坐标,因此,要求函数的最大值与最小值,只要作出函数的图象,求出图象的最高点与最低点的纵坐标即可.
【变式训练1】已知x∈R,定义函数f(x)是y=2-x2,y=x这两个函数中的较小者,则f(x)的最大值为 ( )
A. 2 B. 1
C. -1 D. 无最大值
【解】在同一平面直角坐标系中画出函数y=2-x2,y=x的图象,如图.根据题意,图中实线部分即为函数f(x)的图象.所以当x=1时,f(x)max=1.故选B.
B
【例2】函数y= ,的最大值为________.
思路点拨:求分段函数的最大值,需要先求出每一段在各自范围上的最大值,再比较.注意每段上最大值的求解,需要先判断各段的单调性.也可以通过作出图象来求.
【解】
方法1:当x<1时,函数y=x+3单调递增,且有y<4,无最大值;当x≥1时,函数y=-x+6单调递减,则在x=1处取得最大值,最大值为5.故函数在整个定义域内的最大值为5.
方法2:作出分段函数y= 的图象,如图,由图象可得函数在整个定义域内的最大值为5.
【方法规律】
分段函数的最大(小)值是各段函数最大(小)值中的最大(小)者,或者作出其图象,由图象得出其最大(小)值.
【变式训练2】 求函数y=|x+1|-|x-2|的最大值和最小值.
【解】y=|x+1|-|x-2|=作出函数的图象(图略),由图可知,y∈[-3,3].所以函数的最大值为3,最小值为-3.
【例3】[2021·广东省广州市增城区高一期末改编题] 已知函数f(x)=x2+2ax+1在区间[-1,2]上的最大值为4,求a的值.
思路点拨 求解与二次函数的最大值、最小值有关的问题,应先考虑该函数的定义域,可以采用配方法和图象法求解.
【解】 f(x)=x2+2ax+1=(x+a)2+1-a2,对称轴为直线x=-a,结合二次函数的图象知:当-a≥,即a≤-时,f(x)max=f(-1)=1-2a+1=4,所以a=-1,满足条件;当-a<,即a>-时,f(x)max=f(2)=4+4a+1=4,所以a=-,满足条件.综上所述,a=-1或a=-.
【方法规律】
求解二次函数的最大(小)值,需要综合考虑开口方向和对称轴与定义域区间的位置关系,当二次函数中含有参数时,需根据参数的不同取值进行分类讨论.
【变式训练3】已知函数f(x)=x2-2ax+2,x∈ ,求函数f(x)的最小值.
【解】 f(x)=(x-a)2+2-a2,x∈ .当a≥1时,f(x)在 上单调递减,f(x)min=f(1)=3-2a;当-1
(1) 当a=,x∈[1,2]时,求函数f(x)的值域;
(2) 若对任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
思路点拨(1) 当a=,x∈[1,2]时,f(x)=x++2,是单调递增函数,求出其最大值和最小值,即可得到其值域. (2) 分离参数,将不等式恒成立问题转化为求函数的最值问题来处理.
【解】(1) 当a=,x∈[1,2]时,f(x)=x++2,f(x)在x∈[1,2]上是单调递增,证明如下:设1≤x1
(1) 若函数f(x)在[a,b]上是单调递增,则f(x)min=f(a),f(x)max=f(b),得值域为[f(a),f(b)],若函数f(x)在[a,b]上是减函数,则f(x)min=f(b),f(x)max=f(a),得值域为[f(b),f(a)].
(2) 不等式恒成立问题常可转化为函数的最值问题借助单调性来求解.
课堂反思
通过本节课的学习,你学到了哪些知识?
2.你认为本节课的重点和难点是什么?
随堂演练
1. [教材改编题]函数f(x)= 的最大值是( )
A. B. C. D.
A
2. [2021·湖南省怀化市高一期末]下列函数中,在(0,+∞)上存在最小值的是( )
A. y=(x-1)2 B. y=
C. y=-x2+2x D. y=2x+1
A
3. (多选)[2021·江苏省常州市高一期末]已知函数f(x)= (x∈[3,5]),下列结论中正确的是( )
A. f(x)是增函数 B. f(x)是减函数
C. f(x)的最大值是 D. f(x)的值域是
ACD
4. 已知函数f(x)=其中m>0,若f(x)的最小值为0,则实数m的取值范围是 .
5. [2021·陕西省汉中市汉台中学高三月考]二次函数f(x)=x2-2x+3在[0,m]上有最大值3,最小值1,则实数m的取值范围是 .
[2,4]
(0,4]
同学们再见!
Goodbye Students!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
