2023-2024学年人教版八年级数学上册13.1.2 线段的垂直平分线的性质 同步练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册13.1.2 线段的垂直平分线的性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 493.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 09:13:01 | ||
图片预览


文档简介
13.1.2 线段的垂直平分线的性质 同步练习
一、单选题
1.甲、乙、丙三地如图所示,若想建立一个货物中转仓,使其到甲、乙、丙三地的距离相等,则中转仓的位置应选在( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三边中线的交点 D.三边上高的中点
2..如图,在中,的垂直平分线交于点D,则,这是根据( )
A.到线段两端距离相等的点在线段的垂直平分线上 B.中垂线定义
C.线段垂直平分线上的点到线段两端的距离相等 D.等腰三角形三线合一
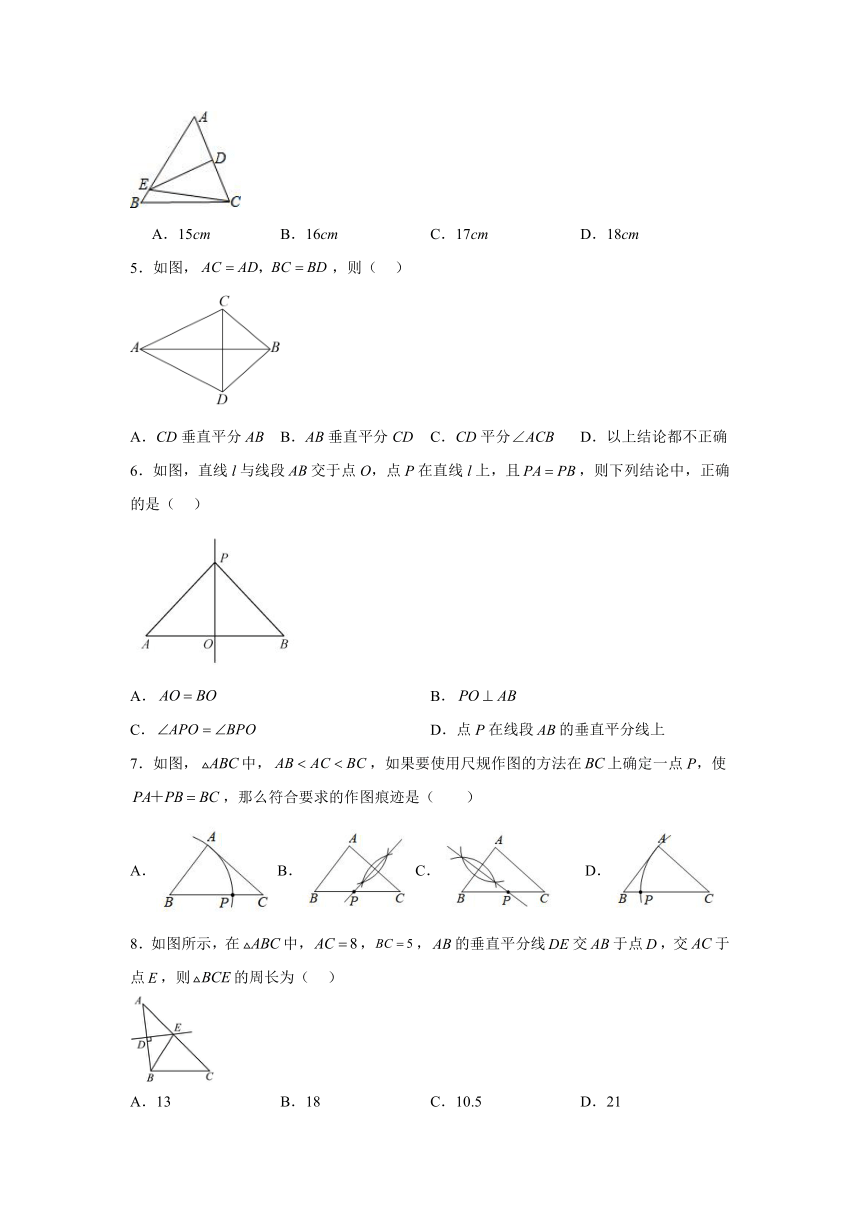
3.如图,在中,以A为圆心,为半径作弧交于点D,再分别以B,D为圆心,大于的长为半径作弧,两弧分别交于M,N,连接交于点E,己知的周长为13,,则的长为( )
A.7 B.8 C.9 D.10
4.如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,AC=7cm,则△EBC的周长为( )
A.15cm B.16cm C.17cm D.18cm
5.如图,,则( )
A.CD垂直平分AB B.AB垂直平分CD C.CD平分∠ACB D.以上结论都不正确
6.如图,直线l与线段交于点O,点P在直线l上,且,则下列结论中,正确的是( )
A. B.
C. D.点P在线段的垂直平分线上
7.如图,中,,如果要使用尺规作图的方法在上确定一点P,使,那么符合要求的作图痕迹是( )
A.B.C. D.
8.如图所示,在中,,,的垂直平分线交于点,交于点,则的周长为( )
A.13 B.18 C.10.5 D.21
二、填空题
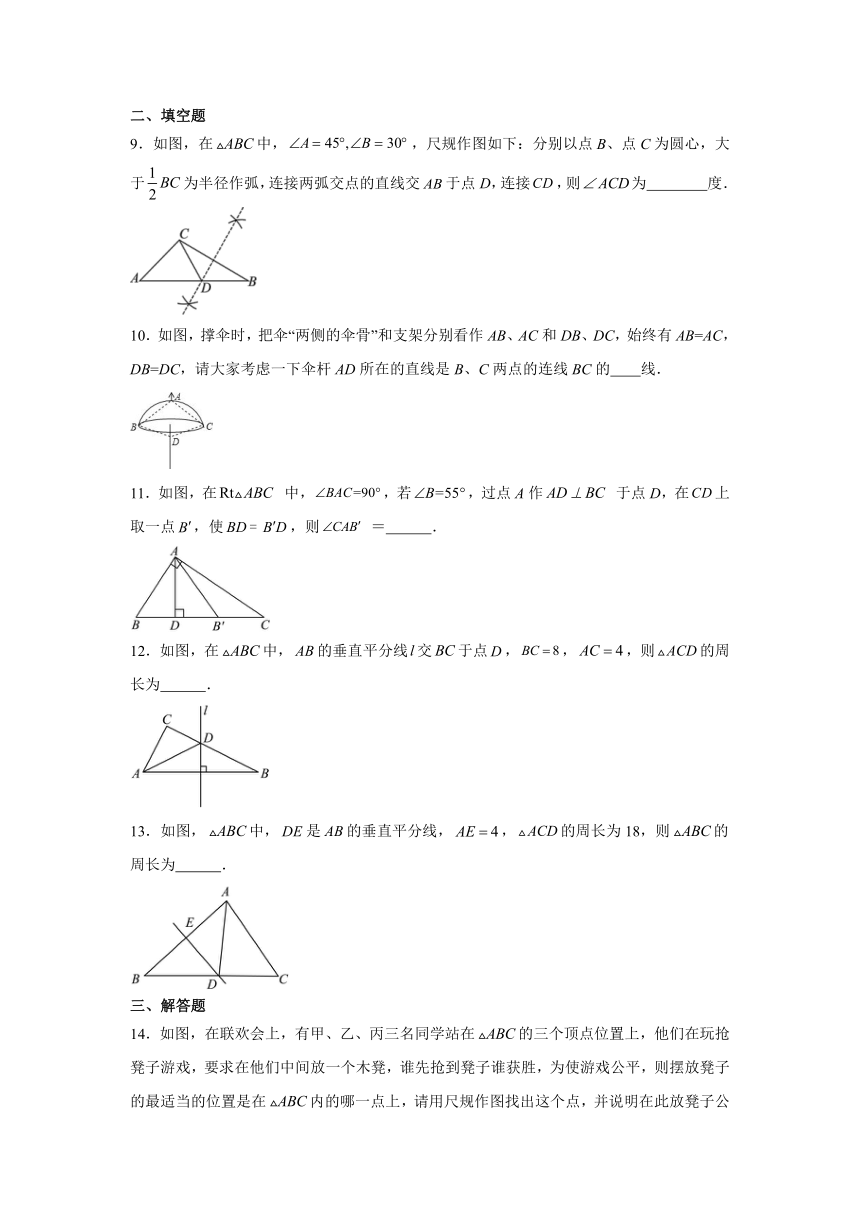
9.如图,在中,,尺规作图如下:分别以点B、点C为圆心,大于为半径作弧,连接两弧交点的直线交于点D,连接,则为 度.
10.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作AB、AC和DB、DC,始终有AB=AC,DB=DC,请大家考虑一下伞杆AD所在的直线是B、C两点的连线BC的 线.
11.如图,在 中,,若,过点A作 于点D,在上取一点,使,则 = .
12.如图,在中,的垂直平分线交于点,,,则的周长为 .
13.如图,中,是的垂直平分线,,的周长为18,则的周长为 .
三、解答题
14.如图,在联欢会上,有甲、乙、丙三名同学站在的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则摆放凳子的最适当的位置是在内的哪一点上,请用尺规作图找出这个点,并说明在此放凳子公平的理由?
15.如图,点是平分线上一点,,,垂足分别是,.
求证:
(1);
(2)是线段的垂直平分线.
16.如图,在中,的垂直平分线交于点,交于点,的垂直平分线交于点,交于点,与相交于点,的周长为.请你解答下列问题:
(1)求的长;
(2)试判断点是否在边的垂直平分线上,并说明理由.
17.如图,在△ABC中,CA=CB,过点A作射线AP∥BC,点M、N分别在边BC、AC上(点M、N不与所在线段端点重合),且BM=AN,连结BN并延长交射线AP于点D,连结MA并延长交AD的垂直平分线于点E,连结ED.
【猜想】如图①,当∠C=30°时,可证△BCN≌△ACM,从而得出∠CBN=∠CAM,进而得出∠BDE的大小为______度.
【探究】如图②,若∠C=β.
(1)求证:△BCN≌△ACM.
(2)∠BDE的大小为______度(用含β的代数式表示).
【应用】如图③,当∠C=120°时,AM平分∠BAC,若AM、BN交于点F,DE=DF,DE=1,则△DEF的面积为______.
参考答案
1--8BCBDB DBA
9.
10.垂直平分
11.
12.
13.26
14.解:∵三角形的三条边的垂直平分线的交点到中间的凳子的距离相等,
∴凳子应放在△ABC的三边中垂线的交点最适当.
如图,分别作AB边和BC边的垂直平分线,交点P即为所求.
15.(1)证明:是的平分线上一点,,,
.
在和中,
,
.
.
(2),
点在的垂直平分线上.
又,
点在的垂直平分线上,
是的垂直平分线.
16.(1)垂直平分,
,
同理,
;
(2)点在边的垂直平分线上,
理由:连接,,,
与是,的垂直平分线,
,,
,
点在边的垂直平分线上.
17.证明:如图,延长ED交BC于点F,交AC于点O,
∵CB=CA,
∴∠ABM=∠BAN,
∵CA=CB,BM=AN,
∴CM=CN,
∵∠C=∠C,
∴△BCN≌△ACM(SAS),
∴∠CBN=∠CAM,
∵E是AD的垂直平分线上的点,
∴EA=ED,
∴∠EAD=∠EDA,
∵AD∥BC,
∴∠EAD=∠EMF,∠EDA=∠EFM,
∴∠BNC=∠BFE,
∴∠NOD+∠BDF=∠C+∠FOC,
∵∠C=30°,∠FOC=∠NOD,
∴∠NDO=30°,
∴∠BDE=150°,
故答案为:150°;
探究:
(1)证明:∵CA=CB,BM=AN,
∴CA﹣AN=CB﹣BM,
∴MC=NC,
在△BCN和△ACM中,,
∴△BCN≌△ACM(SAS);
(2)如图,延长ED交BC于点F,
同理得△BCN≌△ACM(SAS),
∴∠CBN=∠CAM,
同理得:∠BNC=∠AMC=∠BFE,
∴∠BNC+∠NBC=∠NBC+∠BFE,
∴∠ACB=∠BDF=β,
∴∠BDE=180°﹣β.
故答案为:(180﹣β);
应用:
∵∠C=120°,CA=CB,
∴∠BAC=30°,
∵AM平分∠BAC,
∴∠MAC=∠BAC=15°,
∵AP∥BC,
∴∠C=∠CAD=120°,
∴∠EAD=180°﹣∠MAC﹣∠CAD=45°,
由(2)可知,∠BDE=180°﹣120°=60°,∠CBN=∠CAM=∠ADB=15°,
∴∠ADE=45°,
∴∠E=90°,
∵DE=DF,DE=1,
∴DF=2,
∴△DEF的面积为.
故答案为:1.
一、单选题
1.甲、乙、丙三地如图所示,若想建立一个货物中转仓,使其到甲、乙、丙三地的距离相等,则中转仓的位置应选在( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三边中线的交点 D.三边上高的中点
2..如图,在中,的垂直平分线交于点D,则,这是根据( )
A.到线段两端距离相等的点在线段的垂直平分线上 B.中垂线定义
C.线段垂直平分线上的点到线段两端的距离相等 D.等腰三角形三线合一
3.如图,在中,以A为圆心,为半径作弧交于点D,再分别以B,D为圆心,大于的长为半径作弧,两弧分别交于M,N,连接交于点E,己知的周长为13,,则的长为( )
A.7 B.8 C.9 D.10
4.如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,AC=7cm,则△EBC的周长为( )
A.15cm B.16cm C.17cm D.18cm
5.如图,,则( )
A.CD垂直平分AB B.AB垂直平分CD C.CD平分∠ACB D.以上结论都不正确
6.如图,直线l与线段交于点O,点P在直线l上,且,则下列结论中,正确的是( )
A. B.
C. D.点P在线段的垂直平分线上
7.如图,中,,如果要使用尺规作图的方法在上确定一点P,使,那么符合要求的作图痕迹是( )
A.B.C. D.
8.如图所示,在中,,,的垂直平分线交于点,交于点,则的周长为( )
A.13 B.18 C.10.5 D.21
二、填空题
9.如图,在中,,尺规作图如下:分别以点B、点C为圆心,大于为半径作弧,连接两弧交点的直线交于点D,连接,则为 度.
10.如图,撑伞时,把伞“两侧的伞骨”和支架分别看作AB、AC和DB、DC,始终有AB=AC,DB=DC,请大家考虑一下伞杆AD所在的直线是B、C两点的连线BC的 线.
11.如图,在 中,,若,过点A作 于点D,在上取一点,使,则 = .
12.如图,在中,的垂直平分线交于点,,,则的周长为 .
13.如图,中,是的垂直平分线,,的周长为18,则的周长为 .
三、解答题
14.如图,在联欢会上,有甲、乙、丙三名同学站在的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则摆放凳子的最适当的位置是在内的哪一点上,请用尺规作图找出这个点,并说明在此放凳子公平的理由?
15.如图,点是平分线上一点,,,垂足分别是,.
求证:
(1);
(2)是线段的垂直平分线.
16.如图,在中,的垂直平分线交于点,交于点,的垂直平分线交于点,交于点,与相交于点,的周长为.请你解答下列问题:
(1)求的长;
(2)试判断点是否在边的垂直平分线上,并说明理由.
17.如图,在△ABC中,CA=CB,过点A作射线AP∥BC,点M、N分别在边BC、AC上(点M、N不与所在线段端点重合),且BM=AN,连结BN并延长交射线AP于点D,连结MA并延长交AD的垂直平分线于点E,连结ED.
【猜想】如图①,当∠C=30°时,可证△BCN≌△ACM,从而得出∠CBN=∠CAM,进而得出∠BDE的大小为______度.
【探究】如图②,若∠C=β.
(1)求证:△BCN≌△ACM.
(2)∠BDE的大小为______度(用含β的代数式表示).
【应用】如图③,当∠C=120°时,AM平分∠BAC,若AM、BN交于点F,DE=DF,DE=1,则△DEF的面积为______.
参考答案
1--8BCBDB DBA
9.
10.垂直平分
11.
12.
13.26
14.解:∵三角形的三条边的垂直平分线的交点到中间的凳子的距离相等,
∴凳子应放在△ABC的三边中垂线的交点最适当.
如图,分别作AB边和BC边的垂直平分线,交点P即为所求.
15.(1)证明:是的平分线上一点,,,
.
在和中,
,
.
.
(2),
点在的垂直平分线上.
又,
点在的垂直平分线上,
是的垂直平分线.
16.(1)垂直平分,
,
同理,
;
(2)点在边的垂直平分线上,
理由:连接,,,
与是,的垂直平分线,
,,
,
点在边的垂直平分线上.
17.证明:如图,延长ED交BC于点F,交AC于点O,
∵CB=CA,
∴∠ABM=∠BAN,
∵CA=CB,BM=AN,
∴CM=CN,
∵∠C=∠C,
∴△BCN≌△ACM(SAS),
∴∠CBN=∠CAM,
∵E是AD的垂直平分线上的点,
∴EA=ED,
∴∠EAD=∠EDA,
∵AD∥BC,
∴∠EAD=∠EMF,∠EDA=∠EFM,
∴∠BNC=∠BFE,
∴∠NOD+∠BDF=∠C+∠FOC,
∵∠C=30°,∠FOC=∠NOD,
∴∠NDO=30°,
∴∠BDE=150°,
故答案为:150°;
探究:
(1)证明:∵CA=CB,BM=AN,
∴CA﹣AN=CB﹣BM,
∴MC=NC,
在△BCN和△ACM中,,
∴△BCN≌△ACM(SAS);
(2)如图,延长ED交BC于点F,
同理得△BCN≌△ACM(SAS),
∴∠CBN=∠CAM,
同理得:∠BNC=∠AMC=∠BFE,
∴∠BNC+∠NBC=∠NBC+∠BFE,
∴∠ACB=∠BDF=β,
∴∠BDE=180°﹣β.
故答案为:(180﹣β);
应用:
∵∠C=120°,CA=CB,
∴∠BAC=30°,
∵AM平分∠BAC,
∴∠MAC=∠BAC=15°,
∵AP∥BC,
∴∠C=∠CAD=120°,
∴∠EAD=180°﹣∠MAC﹣∠CAD=45°,
由(2)可知,∠BDE=180°﹣120°=60°,∠CBN=∠CAM=∠ADB=15°,
∴∠ADE=45°,
∴∠E=90°,
∵DE=DF,DE=1,
∴DF=2,
∴△DEF的面积为.
故答案为:1.
