切割线定理[下学期]
图片预览

文档简介
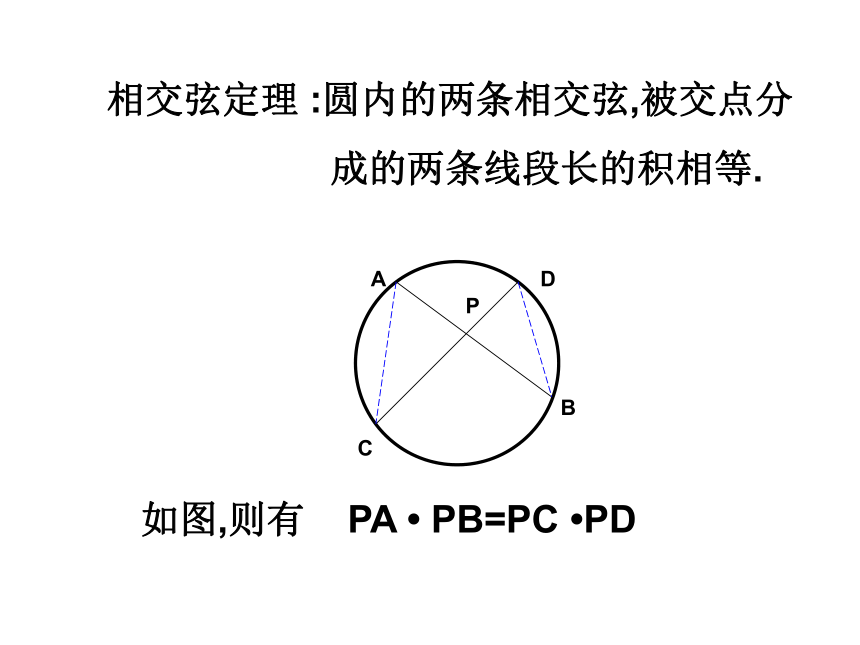
课件17张PPT。切割线定理杭十中 赵玉华相交弦定理 :圆内的两条相交弦,被交点分
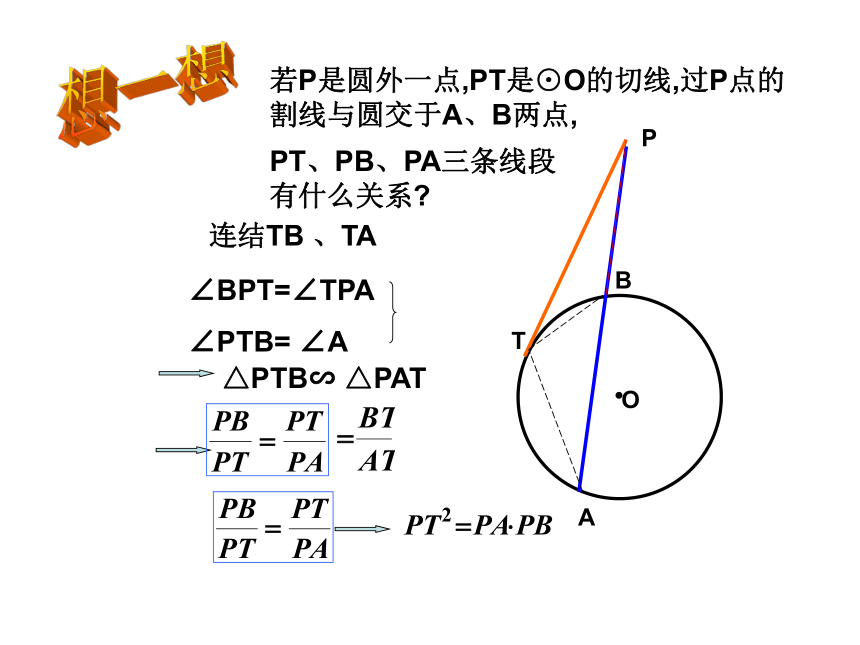
成的两条线段长的积相等.如图,则有 PA ? PB=PC ?PDTPAB?O想一想若P是圆外一点,PT是⊙O的切线,过P点的割线与圆交于A、B两点,PT、PB、PA三条线段有什么关系?∠BPT=∠TPA
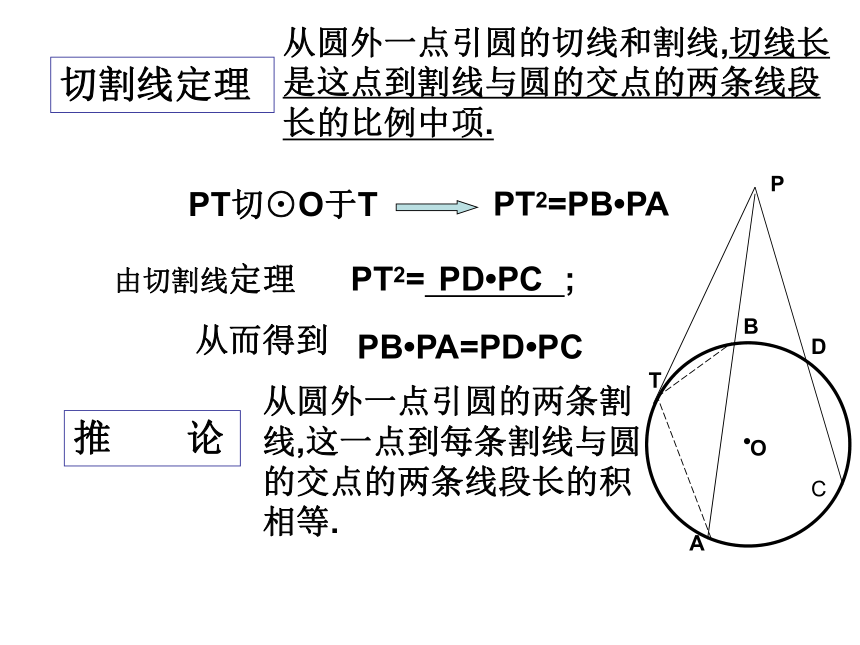
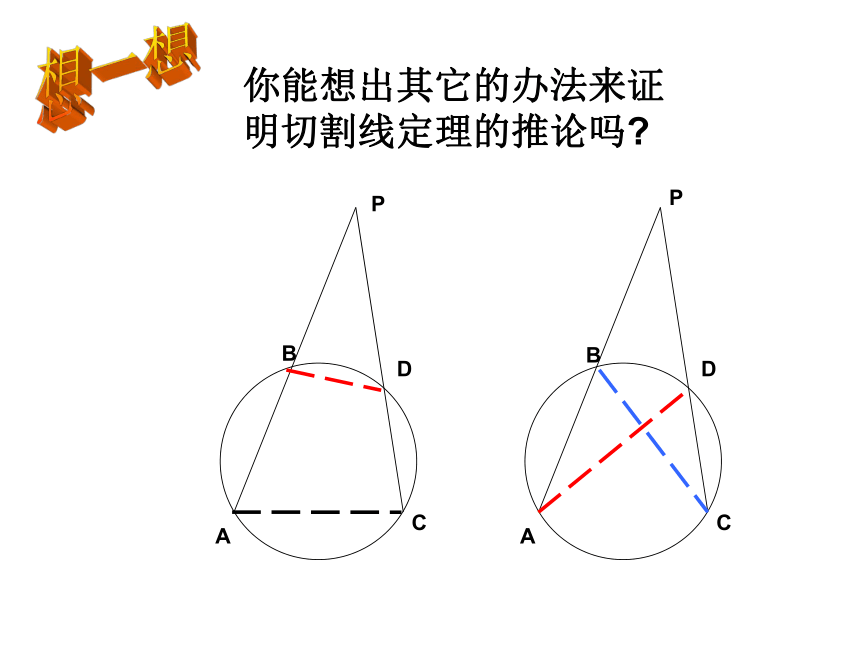
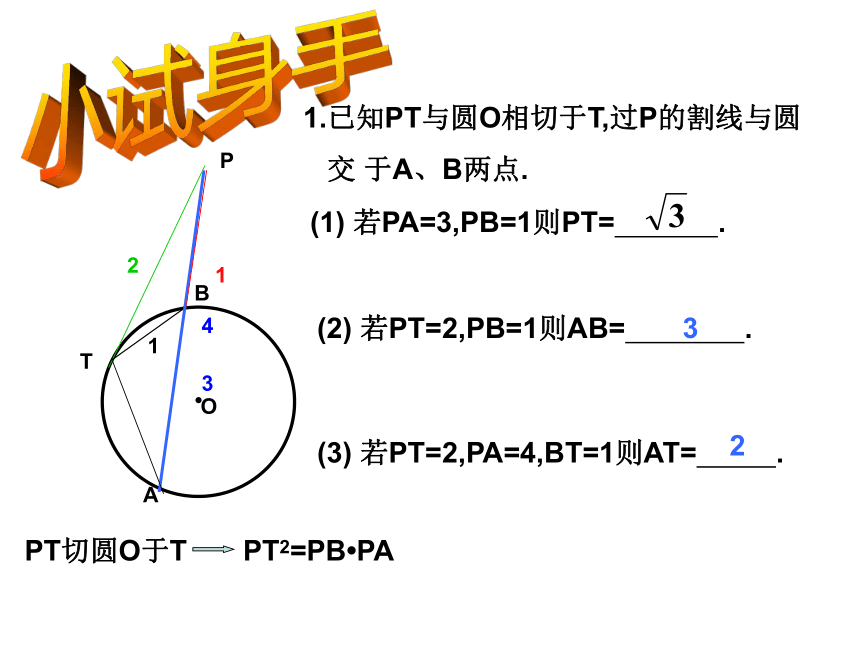
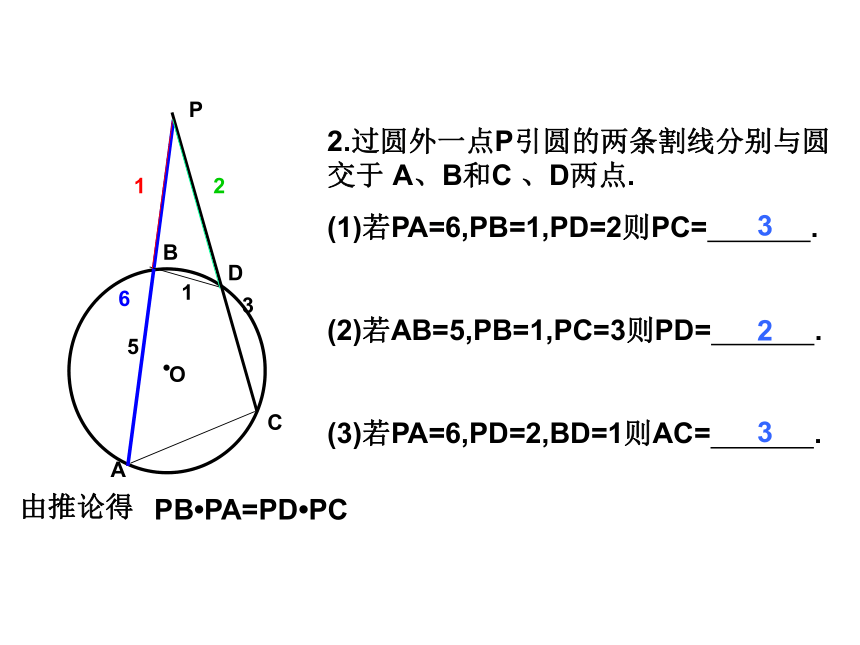
∠PTB= ∠A△PTB∽ △PATPAB?ODC切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆的交点的两条线段长的比例中项.推 论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.T PT2=PB?PA PB?PA=PD?PC从而得到PT切⊙O于T由切割线定理PT2= ;PD?PCPABDC想一想你能想出其它的办法来证明切割线定理的推论吗?(2) 若PT=2,PB=1则AB= . (3) 若PT=2,PA=4,BT=1则AT= .32(1) 若PA=3,PB=1则PT= . 31小试身手2412.过圆外一点P引圆的两条割线分别与圆交于 A、B和C 、D两点.
(1)若PA=6,PB=1,PD=2则PC= .
(2)若AB=5,PB=1,PC=3则PD= .
(3)若PA=6,PD=2,BD=1则AC= . 323PAB?ODCPB?PA=PD?PC由推论得612531例1 如图过圆外一点P作两条割线,分别交圆O于A、B和C、D.
再作圆O切线PE,E为切点,连结CE、DE.已知 AB=3cm,
PA=2cm,CD=4cm。解: BAPCDE ∵AB=3cm, PA=2cm ∴ PB=AB+PA=5(cm)∵CD=4cm, ∴PD=PC+CD=x+4∴x(x+4)=2×5化简,整理得 x2+4x-10=0 由切割线定理,得PE2=PA?PB234x设PC=x∴PE2= 2×5=10
∴PE= (cm). 由切割线定理推论得,PC?PD=PA?PB(1) 求PC,PE的长例1 如图过圆外一点P作两条割线,分别交⊙O于A、B和C、D.再作⊙O
切线PE,E为切点,连结CE、DE.已知AB=3cm,PA=2cm,CD=4cm
.解:由弦切角定理,得∠CEP= ∠D又∵∠CPE=∠EPD,∴△CPE∽△EPD ∴ ∵PD=PC+CDBAPCDE234x(2) 设CE=a,试用含a的代数式表示DEa判断题如图所示,PT切⊙O于T。下面的判断是否正确.PBACDTO(1)PT2=PE?PD ( )(2)PA?PB=PE?PD ( )(3) PA?AB=PE?ED ( )(4) PT2=PC?PO ( )E.PBACO 在上题中,若PO=5,r=2,你能求出
PA和PB的积吗?D思考分析:延长PO交⊙O于DPC=PO-CO=5-2=3PD=PO + OD=5 + 2=7PA?PB=PC?PD=21例2 如图,A是圆O上的一点,过点A的切线交直径
CB的延长线于点P,AD⊥BC ,D为垂足。
求证:D证明: 连结OAPD?PO=PA2PA切圆O于APB?PC=PA2PB?PC=PD?POPA切圆O于AOA⊥PAAD⊥PC1。若过圆外一点P的切线与⊙O相切于T点,P与圆心O的
连线与圆交于A点,若PO=5,半径是4,求切线长PT。
OB练习2。如图,过点A作圆的两条割线分别交⊙O于B,C
和D,E。已知AD=4cm,DE=2cm,CE=5cm,
AB=BC,求AB,BD。DBCEA练习小结1.切割线定理及其推论2.切割线定理及其推论和相交线定理一样
是相似三角形对应边成比例的另一种形
式。3. 应用切割线定理和推论可以运用其乘积
式和比例式关系进行问题的转化。 想一想ABPCDEF(1)如图⊙O1与⊙O2相交于A、B两点,P是
AB的延长线上的一点,过P点的割线分
别与⊙O1、⊙O2交于D、C;E,F。
O1O2 试判断PD?PC是否和PF?PE相等。
为什么?OABST(2)如图A、B是⊙O割线上的两点,AS切⊙O于S,BT切⊙O于T。若AC=BD,则AS和TB有什么关系?CD
成的两条线段长的积相等.如图,则有 PA ? PB=PC ?PDTPAB?O想一想若P是圆外一点,PT是⊙O的切线,过P点的割线与圆交于A、B两点,PT、PB、PA三条线段有什么关系?∠BPT=∠TPA
∠PTB= ∠A△PTB∽ △PATPAB?ODC切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆的交点的两条线段长的比例中项.推 论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.T PT2=PB?PA PB?PA=PD?PC从而得到PT切⊙O于T由切割线定理PT2= ;PD?PCPABDC想一想你能想出其它的办法来证明切割线定理的推论吗?(2) 若PT=2,PB=1则AB= . (3) 若PT=2,PA=4,BT=1则AT= .32(1) 若PA=3,PB=1则PT= . 31小试身手2412.过圆外一点P引圆的两条割线分别与圆交于 A、B和C 、D两点.
(1)若PA=6,PB=1,PD=2则PC= .
(2)若AB=5,PB=1,PC=3则PD= .
(3)若PA=6,PD=2,BD=1则AC= . 323PAB?ODCPB?PA=PD?PC由推论得612531例1 如图过圆外一点P作两条割线,分别交圆O于A、B和C、D.
再作圆O切线PE,E为切点,连结CE、DE.已知 AB=3cm,
PA=2cm,CD=4cm。解: BAPCDE ∵AB=3cm, PA=2cm ∴ PB=AB+PA=5(cm)∵CD=4cm, ∴PD=PC+CD=x+4∴x(x+4)=2×5化简,整理得 x2+4x-10=0 由切割线定理,得PE2=PA?PB234x设PC=x∴PE2= 2×5=10
∴PE= (cm). 由切割线定理推论得,PC?PD=PA?PB(1) 求PC,PE的长例1 如图过圆外一点P作两条割线,分别交⊙O于A、B和C、D.再作⊙O
切线PE,E为切点,连结CE、DE.已知AB=3cm,PA=2cm,CD=4cm
.解:由弦切角定理,得∠CEP= ∠D又∵∠CPE=∠EPD,∴△CPE∽△EPD ∴ ∵PD=PC+CDBAPCDE234x(2) 设CE=a,试用含a的代数式表示DEa判断题如图所示,PT切⊙O于T。下面的判断是否正确.PBACDTO(1)PT2=PE?PD ( )(2)PA?PB=PE?PD ( )(3) PA?AB=PE?ED ( )(4) PT2=PC?PO ( )E.PBACO 在上题中,若PO=5,r=2,你能求出
PA和PB的积吗?D思考分析:延长PO交⊙O于DPC=PO-CO=5-2=3PD=PO + OD=5 + 2=7PA?PB=PC?PD=21例2 如图,A是圆O上的一点,过点A的切线交直径
CB的延长线于点P,AD⊥BC ,D为垂足。
求证:D证明: 连结OAPD?PO=PA2PA切圆O于APB?PC=PA2PB?PC=PD?POPA切圆O于AOA⊥PAAD⊥PC1。若过圆外一点P的切线与⊙O相切于T点,P与圆心O的
连线与圆交于A点,若PO=5,半径是4,求切线长PT。
OB练习2。如图,过点A作圆的两条割线分别交⊙O于B,C
和D,E。已知AD=4cm,DE=2cm,CE=5cm,
AB=BC,求AB,BD。DBCEA练习小结1.切割线定理及其推论2.切割线定理及其推论和相交线定理一样
是相似三角形对应边成比例的另一种形
式。3. 应用切割线定理和推论可以运用其乘积
式和比例式关系进行问题的转化。 想一想ABPCDEF(1)如图⊙O1与⊙O2相交于A、B两点,P是
AB的延长线上的一点,过P点的割线分
别与⊙O1、⊙O2交于D、C;E,F。
O1O2 试判断PD?PC是否和PF?PE相等。
为什么?OABST(2)如图A、B是⊙O割线上的两点,AS切⊙O于S,BT切⊙O于T。若AC=BD,则AS和TB有什么关系?CD
同课章节目录
