4.1.2 图形的坐标变化与平移变换同步练习(含解析)
文档属性
| 名称 | 4.1.2 图形的坐标变化与平移变换同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
1 图形的平移
第2课时 图形的坐标变化与平移变换
刷基础
知识点1 由图形的平移分析点的坐标变化
1.在平面直角坐标系中,将点A(-3,2)向下平移3个单位后得到的点 A 的坐标为( )
A.(-3,5) B.(-3,3) C.(-3,-1) D.(0,2)
2.如图,在平面直角坐标系中,点A 的坐标是(1,2),将线段 OA 向右平移4个单位长度,得到线段BC,点A 的对应点C的坐标是____________.
3.在平面直角坐标系中,已知线段 MN的两个端点的坐标分别是M(-4,-1),N(0,1),将线段 MN平移后得到线段M'N'(点 M,N分别平移到点 M',N'的位置),若点M'的坐标为(-2,2),则点 N'的坐标为___________.
4如图,点 A 的坐标为(1,3),点 B 在x轴上,把△OAB沿x轴向右平移得到△ECD,若平行四边形 ABDC 的 面积为 9,则点 C 的 坐标为__________.
5如图,平面直角坐标系中,A,B的坐标分别为(2,0),(0,1),若将线段 AB平移至A1B1,则的值为______________.
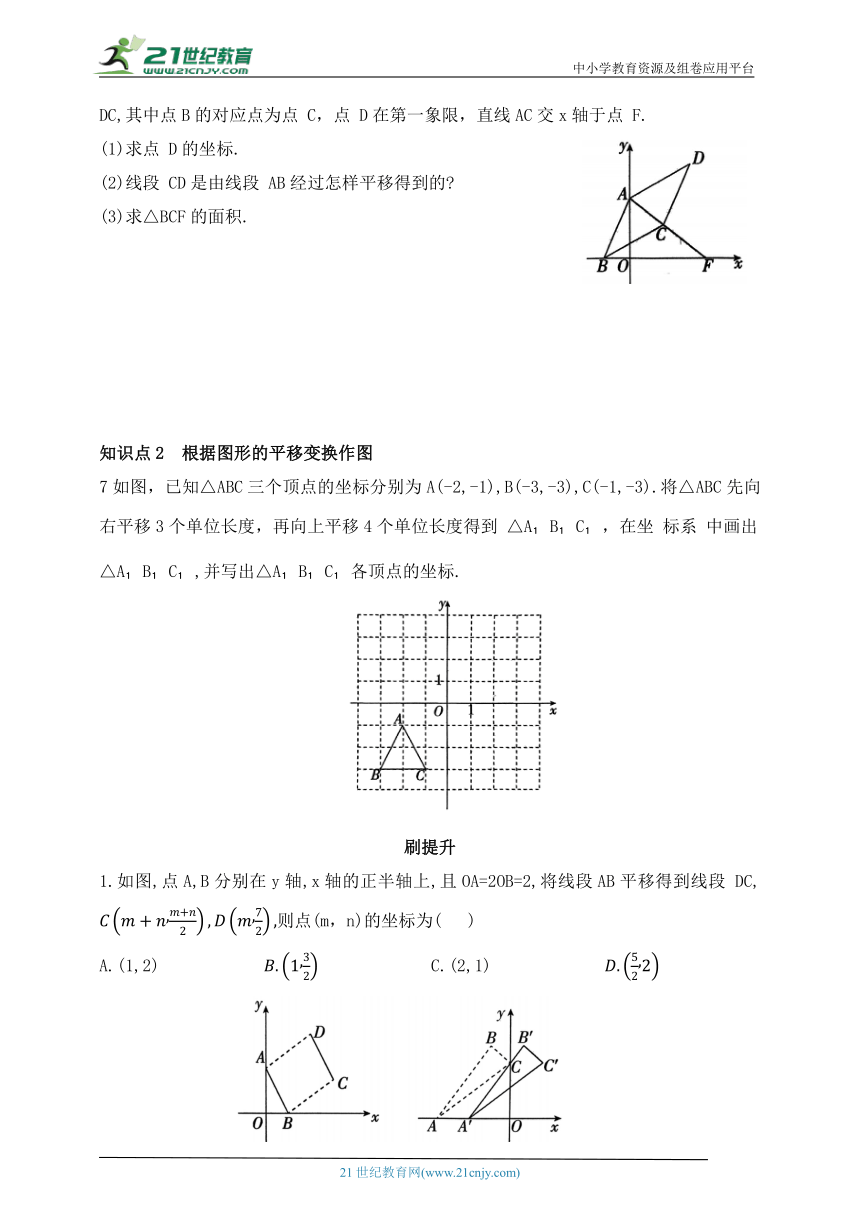
6.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB 经过平移得到线段 DC,其中点B的对应点为点 C,点 D在第一象限,直线AC交x轴于点 F.
(1)求点 D的坐标.
(2)线段 CD是由线段 AB经过怎样平移得到的
(3)求△BCF的面积.
知识点2 根据图形的平移变换作图
7如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).将△ABC先向右平移3个单位长度,再向上平移4个单位长度得到 △A B C ,在坐 标系 中画出
△A B C ,并写出△A B C 各顶点的坐标.
刷提升
1.如图,点A,B分别在y轴,x轴的正半轴上,且OA=2OB=2,将线段AB平移得到线段 DC, 则点(m,n)的坐标为( )
A.(1,2) C.(2,1)
第1题图 第2题图
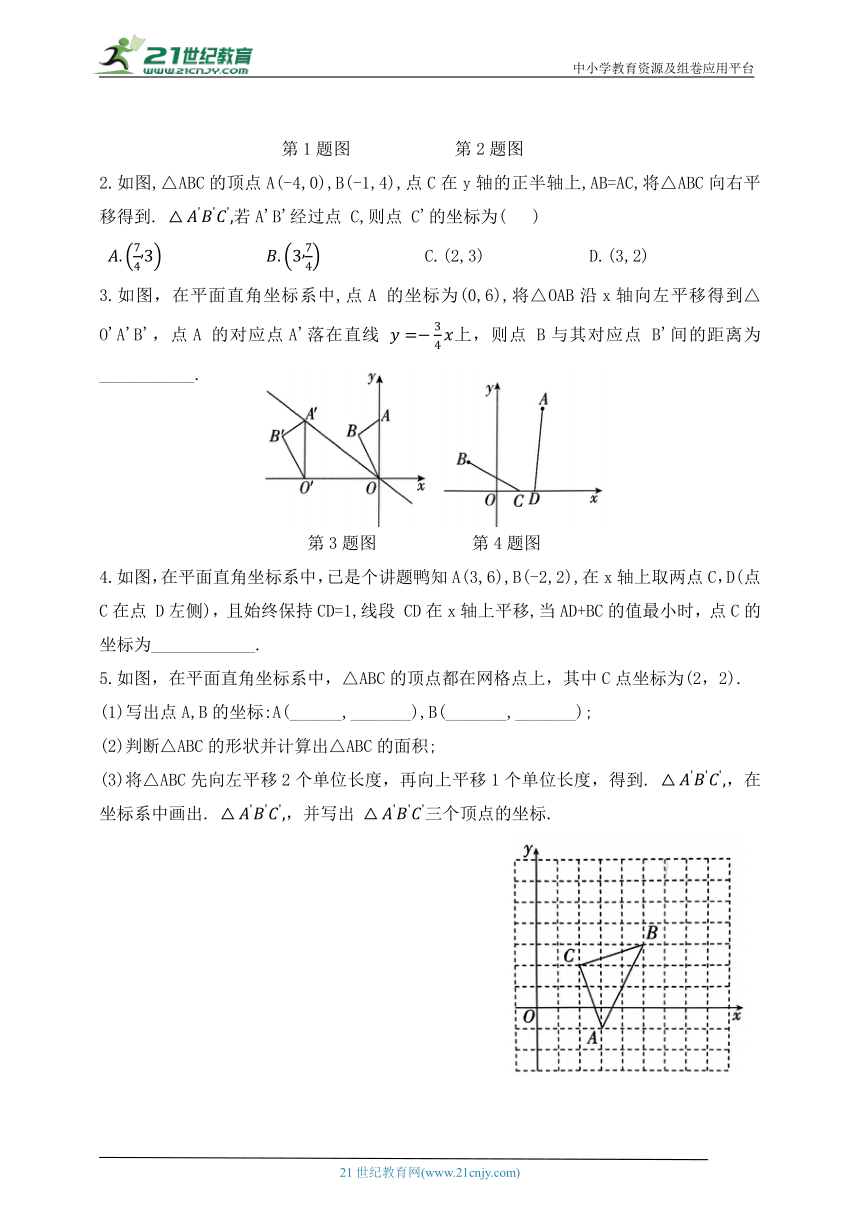
2.如图,△ABC的顶点A(-4,0),B(-1,4),点C在y轴的正半轴上,AB=AC,将△ABC向右平移得到. 若A'B'经过点 C,则点 C'的坐标为( )
C.(2,3) D.(3,2)
3.如图,在平面直角坐标系中,点A 的坐标为(0,6),将△OAB沿x轴向左平移得到△O'A'B',点A 的对应点A'落在直线 上,则点 B与其对应点 B'间的距离为___________.
第3题图 第4题图
4.如图,在平面直角坐标系中,已是个讲题鸭知A(3,6),B(-2,2),在x轴上取两点C,D(点C在点 D左侧),且始终保持CD=1,线段 CD在x轴上平移,当AD+BC的值最小时,点C的坐标为____________.
5.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(2,2).
(1)写出点A,B的坐标:A(______,_______),B(_______,_______);
(2)判断△ABC的形状并计算出△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到. ,在坐标系中画出. ,并写出 三个顶点的坐标.
刷素养
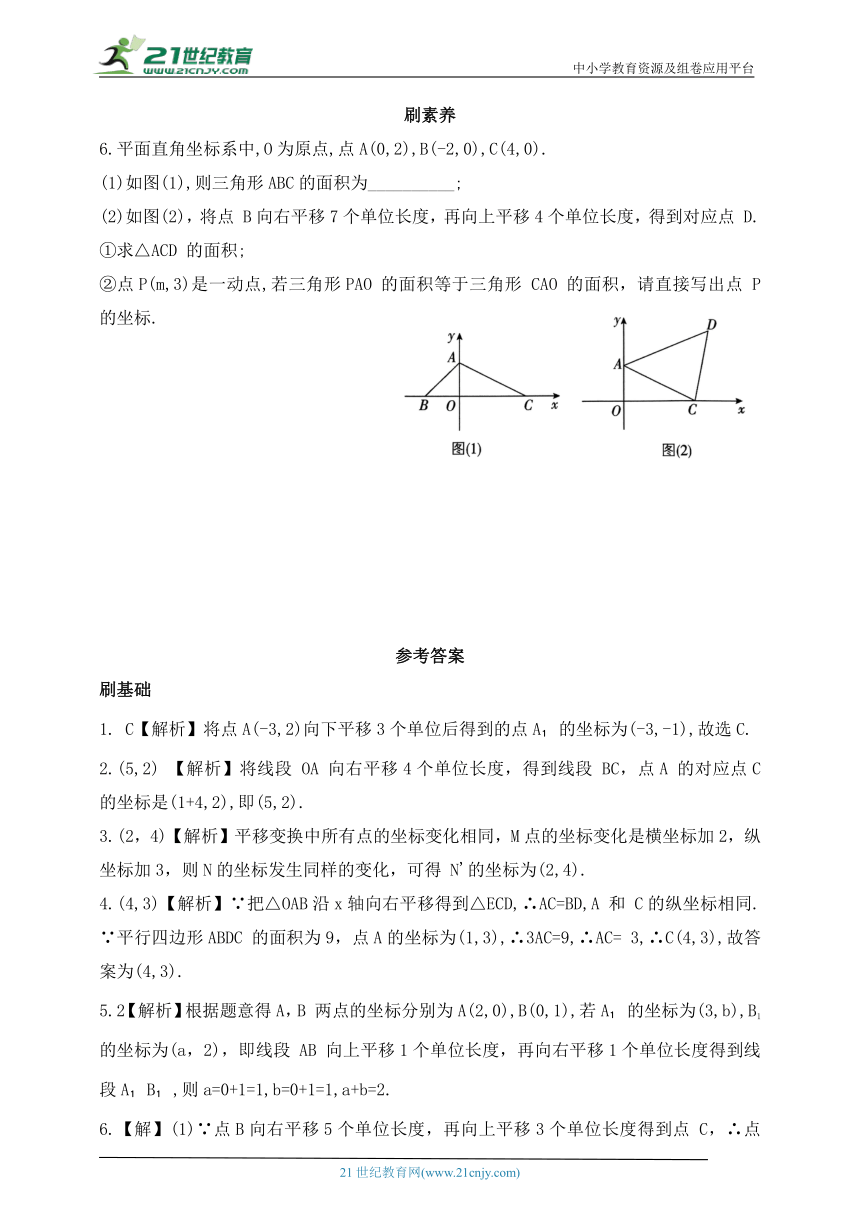
6.平面直角坐标系中,O为原点,点A(0,2),B(-2,0),C(4,0).
(1)如图(1),则三角形ABC的面积为__________;
(2)如图(2),将点 B向右平移7个单位长度,再向上平移4个单位长度,得到对应点 D.
①求△ACD 的面积;
②点P(m,3)是一动点,若三角形PAO 的面积等于三角形 CAO 的面积,请直接写出点 P的坐标.
参考答案
刷基础
1. C【解析】将点A(-3,2)向下平移3个单位后得到的点A 的坐标为(-3,-1),故选C.
2.(5,2) 【解析】将线段 OA 向右平移4个单位长度,得到线段 BC,点A 的对应点C的坐标是(1+4,2),即(5,2).
3.(2,4)【解析】平移变换中所有点的坐标变化相同,M点的坐标变化是横坐标加2,纵坐标加3,则N的坐标发生同样的变化,可得 N'的坐标为(2,4).
4.(4,3)【解析】∵把△OAB沿x轴向右平移得到△ECD,∴AC=BD,A 和 C的纵坐标相同.∵平行四边形ABDC 的面积为9,点A的坐标为(1,3),∴3AC=9,∴AC= 3,∴C(4,3),故答案为(4,3).
5.2【解析】根据题意得A,B 两点的坐标分别为A(2,0),B(0,1),若A 的坐标为(3,b),B1的坐标为(a,2),即线段 AB 向上平移1个单位长度,再向右平移1个单位长度得到线段A B ,则a=0+1=1,b=0+1=1,a+b=2.
6.【解】(1)∵点B向右平移5个单位长度,再向上平移3个单位长度得到点 C,∴点A(0,5)向右平移5个单位长度,再向上平移3个单位长度得到点 D(5,8).
(2)先向右平移5个单位长度,再向上平移3个单位长度(或先向上平移3个单位长度,再向右平移5个单位长度).
(3)设直线 AC 的表达式为y=kx+b(k≠0),则有 解得
∴直线AC 的表达式为 ∴点F的坐标为
7.【解】△A B C 如图所示.
A (1,3),B (0,1),C (2,1).
刷提升
1. C 【解析】由题意得 A(0,2),B(1,0),
点(m,n)的坐标变为(2,1).
2. A【解析】连接 CC'.∵A(-4,0),B(-1,4),∴易得直线AB 的表达式为 5,∴AB=AC = 5.又∵OA=4,∴ OC = 3,∴C(0,3).∵A'B'∥AB,∴直线A'B'的表达式为 故选A.
3.8【解析】由题意可知,点A 移动到点A'位置时,纵坐标不变,∴点A'的纵坐标为6.∵点A'在直线 上, 解得x=-8,∴△OAB沿x轴向左平移了8个单位长度得到△O'A'B',∴点B与其对应点 B'间的距离为8.故答案为8.
4.(-1,0)【解析】如图,把点A(3,6)向左平移1个单位得到点A'(2,6),作点B关于x轴的对称点 B',连接B'A'交x轴于C,在x轴上取点D(点C在点D左侧),使 CD=1,连接AD,则 AD+BC 的值最小.
∵B(-2,2),∴B'(-2,-2).设直线B'A'的表达式为y=kx+b(解得
直线B'A'的表达式为y=2x+2,当y=0时,x=-1,∴C(-1,0),故答案为(-1,0).
5.(1)3 -1 5 3
【解】(2)△ABC是等腰直角三角形.∵AC=即
△ABC 是等腰直角三角形. 故△ABC 的面积为5.
如图所示. 4),C'(0,3).
刷素养
6.【解】(1)∵A(0,2),B(-2,0),C(4,0),∴OA=(2+4)×2=6.故答案为 6.
(2)①∵点B(-2,0)向右平移7个单位长度,再向上平移4个单位长度,得到对应点 D∴D(5,4).连接 OD,如图.
②P(-4,3)或(4,3).∵三角形PAO 的面积等于三角形CAO 的面积,∴ 4,解得 m=±4,∴P(-4,3)或(4,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 图形的平移与旋转
1 图形的平移
第2课时 图形的坐标变化与平移变换
刷基础
知识点1 由图形的平移分析点的坐标变化
1.在平面直角坐标系中,将点A(-3,2)向下平移3个单位后得到的点 A 的坐标为( )
A.(-3,5) B.(-3,3) C.(-3,-1) D.(0,2)
2.如图,在平面直角坐标系中,点A 的坐标是(1,2),将线段 OA 向右平移4个单位长度,得到线段BC,点A 的对应点C的坐标是____________.
3.在平面直角坐标系中,已知线段 MN的两个端点的坐标分别是M(-4,-1),N(0,1),将线段 MN平移后得到线段M'N'(点 M,N分别平移到点 M',N'的位置),若点M'的坐标为(-2,2),则点 N'的坐标为___________.
4如图,点 A 的坐标为(1,3),点 B 在x轴上,把△OAB沿x轴向右平移得到△ECD,若平行四边形 ABDC 的 面积为 9,则点 C 的 坐标为__________.
5如图,平面直角坐标系中,A,B的坐标分别为(2,0),(0,1),若将线段 AB平移至A1B1,则的值为______________.
6.如图,在平面直角坐标系中,点A(0,5),B(-2,0),C(3,3),线段AB 经过平移得到线段 DC,其中点B的对应点为点 C,点 D在第一象限,直线AC交x轴于点 F.
(1)求点 D的坐标.
(2)线段 CD是由线段 AB经过怎样平移得到的
(3)求△BCF的面积.
知识点2 根据图形的平移变换作图
7如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).将△ABC先向右平移3个单位长度,再向上平移4个单位长度得到 △A B C ,在坐 标系 中画出
△A B C ,并写出△A B C 各顶点的坐标.
刷提升
1.如图,点A,B分别在y轴,x轴的正半轴上,且OA=2OB=2,将线段AB平移得到线段 DC, 则点(m,n)的坐标为( )
A.(1,2) C.(2,1)
第1题图 第2题图
2.如图,△ABC的顶点A(-4,0),B(-1,4),点C在y轴的正半轴上,AB=AC,将△ABC向右平移得到. 若A'B'经过点 C,则点 C'的坐标为( )
C.(2,3) D.(3,2)
3.如图,在平面直角坐标系中,点A 的坐标为(0,6),将△OAB沿x轴向左平移得到△O'A'B',点A 的对应点A'落在直线 上,则点 B与其对应点 B'间的距离为___________.
第3题图 第4题图
4.如图,在平面直角坐标系中,已是个讲题鸭知A(3,6),B(-2,2),在x轴上取两点C,D(点C在点 D左侧),且始终保持CD=1,线段 CD在x轴上平移,当AD+BC的值最小时,点C的坐标为____________.
5.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(2,2).
(1)写出点A,B的坐标:A(______,_______),B(_______,_______);
(2)判断△ABC的形状并计算出△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到. ,在坐标系中画出. ,并写出 三个顶点的坐标.
刷素养
6.平面直角坐标系中,O为原点,点A(0,2),B(-2,0),C(4,0).
(1)如图(1),则三角形ABC的面积为__________;
(2)如图(2),将点 B向右平移7个单位长度,再向上平移4个单位长度,得到对应点 D.
①求△ACD 的面积;
②点P(m,3)是一动点,若三角形PAO 的面积等于三角形 CAO 的面积,请直接写出点 P的坐标.
参考答案
刷基础
1. C【解析】将点A(-3,2)向下平移3个单位后得到的点A 的坐标为(-3,-1),故选C.
2.(5,2) 【解析】将线段 OA 向右平移4个单位长度,得到线段 BC,点A 的对应点C的坐标是(1+4,2),即(5,2).
3.(2,4)【解析】平移变换中所有点的坐标变化相同,M点的坐标变化是横坐标加2,纵坐标加3,则N的坐标发生同样的变化,可得 N'的坐标为(2,4).
4.(4,3)【解析】∵把△OAB沿x轴向右平移得到△ECD,∴AC=BD,A 和 C的纵坐标相同.∵平行四边形ABDC 的面积为9,点A的坐标为(1,3),∴3AC=9,∴AC= 3,∴C(4,3),故答案为(4,3).
5.2【解析】根据题意得A,B 两点的坐标分别为A(2,0),B(0,1),若A 的坐标为(3,b),B1的坐标为(a,2),即线段 AB 向上平移1个单位长度,再向右平移1个单位长度得到线段A B ,则a=0+1=1,b=0+1=1,a+b=2.
6.【解】(1)∵点B向右平移5个单位长度,再向上平移3个单位长度得到点 C,∴点A(0,5)向右平移5个单位长度,再向上平移3个单位长度得到点 D(5,8).
(2)先向右平移5个单位长度,再向上平移3个单位长度(或先向上平移3个单位长度,再向右平移5个单位长度).
(3)设直线 AC 的表达式为y=kx+b(k≠0),则有 解得
∴直线AC 的表达式为 ∴点F的坐标为
7.【解】△A B C 如图所示.
A (1,3),B (0,1),C (2,1).
刷提升
1. C 【解析】由题意得 A(0,2),B(1,0),
点(m,n)的坐标变为(2,1).
2. A【解析】连接 CC'.∵A(-4,0),B(-1,4),∴易得直线AB 的表达式为 5,∴AB=AC = 5.又∵OA=4,∴ OC = 3,∴C(0,3).∵A'B'∥AB,∴直线A'B'的表达式为 故选A.
3.8【解析】由题意可知,点A 移动到点A'位置时,纵坐标不变,∴点A'的纵坐标为6.∵点A'在直线 上, 解得x=-8,∴△OAB沿x轴向左平移了8个单位长度得到△O'A'B',∴点B与其对应点 B'间的距离为8.故答案为8.
4.(-1,0)【解析】如图,把点A(3,6)向左平移1个单位得到点A'(2,6),作点B关于x轴的对称点 B',连接B'A'交x轴于C,在x轴上取点D(点C在点D左侧),使 CD=1,连接AD,则 AD+BC 的值最小.
∵B(-2,2),∴B'(-2,-2).设直线B'A'的表达式为y=kx+b(解得
直线B'A'的表达式为y=2x+2,当y=0时,x=-1,∴C(-1,0),故答案为(-1,0).
5.(1)3 -1 5 3
【解】(2)△ABC是等腰直角三角形.∵AC=即
△ABC 是等腰直角三角形. 故△ABC 的面积为5.
如图所示. 4),C'(0,3).
刷素养
6.【解】(1)∵A(0,2),B(-2,0),C(4,0),∴OA=(2+4)×2=6.故答案为 6.
(2)①∵点B(-2,0)向右平移7个单位长度,再向上平移4个单位长度,得到对应点 D∴D(5,4).连接 OD,如图.
②P(-4,3)或(4,3).∵三角形PAO 的面积等于三角形CAO 的面积,∴ 4,解得 m=±4,∴P(-4,3)或(4,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
