4.2.2 旋转变换与作图同步练习(含解析)
文档属性
| 名称 | 4.2.2 旋转变换与作图同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-05 21:30:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 图形的平移与旋转
2 图形的旋转
第2课时 旋转变换与作图
刷提升
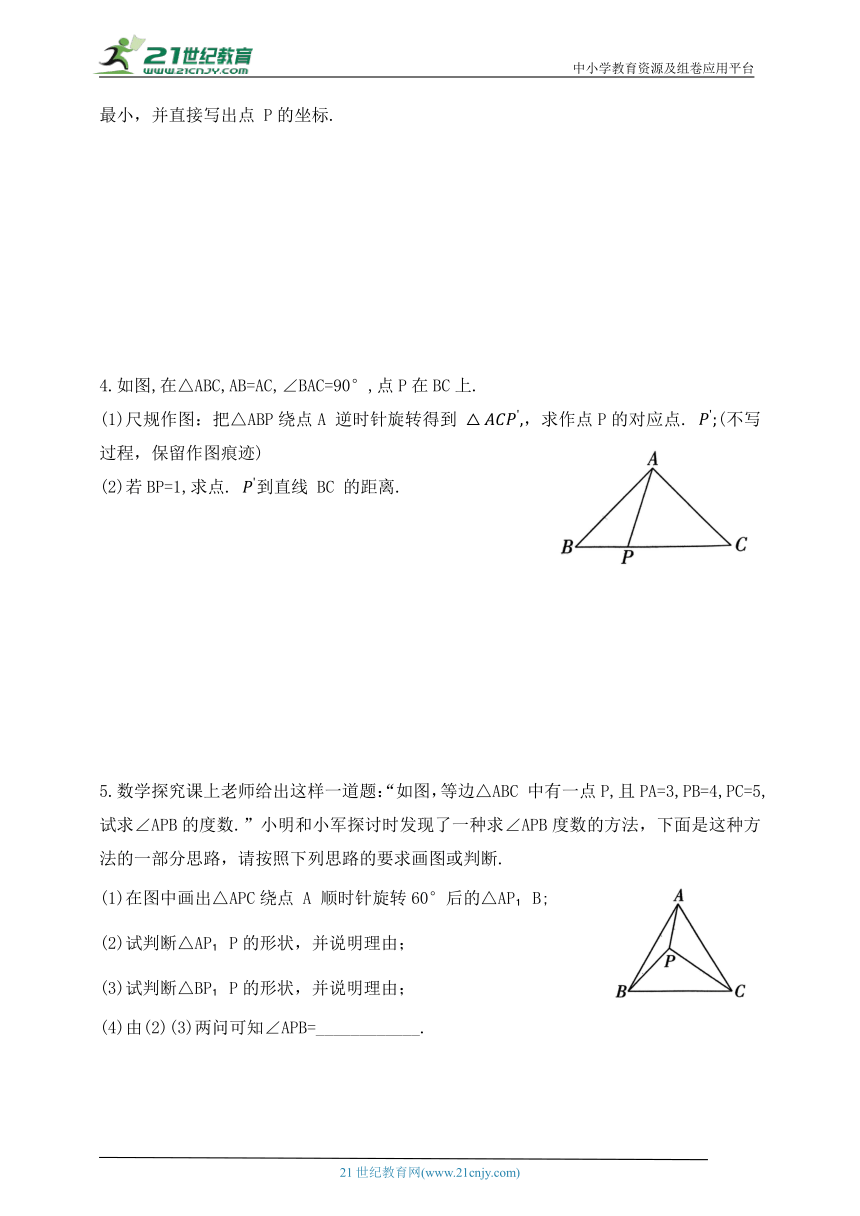
1.如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段 AB与线段 CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是___________.
2.在平面直角坐标系中,△OAB的位置如图所示,将△OAB 绕点O顺时针旋转 90°得 △OA1B1;再将△OA B 绕点O顺时针旋转 90°得△OA B ;再将△OA B 绕点 O顺时针旋转90°得△OA B ;…;依次类推,第 2021 次旋转得到 则顶点A的对应点A 的坐标是____________.
3.△ABC在平面直角坐标系xOy中的位置如图所示,点A(-2,3),点 B(-4,0),点 C(-1,1)为△ABC的顶点.
(1)将△ABC绕原点 O 逆时针旋转90°后得到△A1B1C1,请画出△A B C ;
(2)将△A B C 向右平移5个单位得到△A B C ,作出平移后的△A B C ;
(3)在x轴上求作一点P,(保留作图痕迹)使PB +PA 的值最小,并直接写出点 P的坐标.
4.如图,在△ABC,AB=AC,∠BAC=90°,点P在BC上.
(1)尺规作图:把△ABP绕点A 逆时针旋转得到 ,求作点P的对应点. (不写过程,保留作图痕迹)
(2)若BP=1,求点. 到直线 BC 的距离.
5.数学探究课上老师给出这样一道题:“如图,等边△ABC 中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路的要求画图或判断.
(1)在图中画出△APC绕点 A 顺时针旋转60°后的△AP B;
(2)试判断△AP P的形状,并说明理由;
(3)试判断△BP P的形状,并说明理由;
(4)由(2)(3)两问可知∠APB=____________.
参考答案
刷提升
1.(1,1)或(4,4) 【解析】由 A(-1,5),B(3,3)可确定坐标原点,如图(1)、图(2)所示. 由题意对应点无法确定,因此分情况讨论如下:①当点A的对应点为点C时,连接AC,BD,分别作线段AC,BD的垂直平分线交于点E,如图(1)所示,则E点的坐标为(1,1).②当点A的对应点为点 D时,连接AD,BC,分别作线段 AD,BC 的垂直平分线交于点M,如图(2)所示,则 M点的坐标为(4,4).综上所述,这个旋转中心的坐标为(1,1)或(4,4).
2.(2,-1)【解析】将△OAB 绕点O 顺时针旋转90°得△OA B ,此时,点 A 的坐标为(2,-1);再将△OA B 绕点 O 顺时针旋转90°得△OA B ,此时,点A 的坐标为(-1,-2);再将△OA B 绕点 O 顺时针旋转 90°得△OA B ,此时,点A 的坐标为(-2,1);再将△OA B 绕点 O 顺时针旋转90°得△OA B ,此时,点A 的坐标为(1,2). 由此可知,每旋转4次为一个循环. ∴第2021次旋转得到 ,则顶点A的对应点A 的坐标与点A 的坐标相同,
为(2,-1).故答案为(2,-1).
3.【解】(1)如图,△A B C 即为所求.
(2)如图,△A B C 即为所求.
(3)如图,点P 即为所求,坐标为 作点B 关于x轴的对称点 B ,则B (0,4).设直线A B 的表达式为 y=kx+b(k≠0),将A (2,-2),B (0,4)代入上式,得 解得∴直线A B 的表达式为y=-3x+4.
令y=0,则-3x+4=0,解得
4.【解】(1)如图,点 P'即为所作.
(2)∵ AB = AC,∠BAC=90°,∴∠B=∠ACB=45°.
∵△ABP绕点A逆时针旋转得到
∴P'C⊥BC,∴点P'到直线 BC 的距离为 1.
5.【解】(1)如图,△AP B为所作.
(2)△AP P为等边三角形.理由如下:
∵△APC 绕点 A 顺时BC针旋转 60°后得到△AP B,∴AP =AP,∠PAP =60°,
∴△AP P为等边三角形.
(3)△BP P为直角三角形.理由如下:
∵△APC绕点 A 顺时针旋转 60°后得到△AP B,∴BP =PC=5.
∵△AP P为等边三角形,∴
∴△BP P为直角三角形.
(4)∵△AP P为等边三角形,∴∠APP =60°.
又∵∠BPP =90°,∴∠APB=90°+60°=150°,
故答案为150°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 图形的平移与旋转
2 图形的旋转
第2课时 旋转变换与作图
刷提升
1.如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段 AB与线段 CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是___________.
2.在平面直角坐标系中,△OAB的位置如图所示,将△OAB 绕点O顺时针旋转 90°得 △OA1B1;再将△OA B 绕点O顺时针旋转 90°得△OA B ;再将△OA B 绕点 O顺时针旋转90°得△OA B ;…;依次类推,第 2021 次旋转得到 则顶点A的对应点A 的坐标是____________.
3.△ABC在平面直角坐标系xOy中的位置如图所示,点A(-2,3),点 B(-4,0),点 C(-1,1)为△ABC的顶点.
(1)将△ABC绕原点 O 逆时针旋转90°后得到△A1B1C1,请画出△A B C ;
(2)将△A B C 向右平移5个单位得到△A B C ,作出平移后的△A B C ;
(3)在x轴上求作一点P,(保留作图痕迹)使PB +PA 的值最小,并直接写出点 P的坐标.
4.如图,在△ABC,AB=AC,∠BAC=90°,点P在BC上.
(1)尺规作图:把△ABP绕点A 逆时针旋转得到 ,求作点P的对应点. (不写过程,保留作图痕迹)
(2)若BP=1,求点. 到直线 BC 的距离.
5.数学探究课上老师给出这样一道题:“如图,等边△ABC 中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路的要求画图或判断.
(1)在图中画出△APC绕点 A 顺时针旋转60°后的△AP B;
(2)试判断△AP P的形状,并说明理由;
(3)试判断△BP P的形状,并说明理由;
(4)由(2)(3)两问可知∠APB=____________.
参考答案
刷提升
1.(1,1)或(4,4) 【解析】由 A(-1,5),B(3,3)可确定坐标原点,如图(1)、图(2)所示. 由题意对应点无法确定,因此分情况讨论如下:①当点A的对应点为点C时,连接AC,BD,分别作线段AC,BD的垂直平分线交于点E,如图(1)所示,则E点的坐标为(1,1).②当点A的对应点为点 D时,连接AD,BC,分别作线段 AD,BC 的垂直平分线交于点M,如图(2)所示,则 M点的坐标为(4,4).综上所述,这个旋转中心的坐标为(1,1)或(4,4).
2.(2,-1)【解析】将△OAB 绕点O 顺时针旋转90°得△OA B ,此时,点 A 的坐标为(2,-1);再将△OA B 绕点 O 顺时针旋转90°得△OA B ,此时,点A 的坐标为(-1,-2);再将△OA B 绕点 O 顺时针旋转 90°得△OA B ,此时,点A 的坐标为(-2,1);再将△OA B 绕点 O 顺时针旋转90°得△OA B ,此时,点A 的坐标为(1,2). 由此可知,每旋转4次为一个循环. ∴第2021次旋转得到 ,则顶点A的对应点A 的坐标与点A 的坐标相同,
为(2,-1).故答案为(2,-1).
3.【解】(1)如图,△A B C 即为所求.
(2)如图,△A B C 即为所求.
(3)如图,点P 即为所求,坐标为 作点B 关于x轴的对称点 B ,则B (0,4).设直线A B 的表达式为 y=kx+b(k≠0),将A (2,-2),B (0,4)代入上式,得 解得∴直线A B 的表达式为y=-3x+4.
令y=0,则-3x+4=0,解得
4.【解】(1)如图,点 P'即为所作.
(2)∵ AB = AC,∠BAC=90°,∴∠B=∠ACB=45°.
∵△ABP绕点A逆时针旋转得到
∴P'C⊥BC,∴点P'到直线 BC 的距离为 1.
5.【解】(1)如图,△AP B为所作.
(2)△AP P为等边三角形.理由如下:
∵△APC 绕点 A 顺时BC针旋转 60°后得到△AP B,∴AP =AP,∠PAP =60°,
∴△AP P为等边三角形.
(3)△BP P为直角三角形.理由如下:
∵△APC绕点 A 顺时针旋转 60°后得到△AP B,∴BP =PC=5.
∵△AP P为等边三角形,∴
∴△BP P为直角三角形.
(4)∵△AP P为等边三角形,∴∠APP =60°.
又∵∠BPP =90°,∴∠APB=90°+60°=150°,
故答案为150°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
