北师大版数学九上第一章1.1菱形的性质与判定 测试卷B卷(含解析)
文档属性
| 名称 | 北师大版数学九上第一章1.1菱形的性质与判定 测试卷B卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 611.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 09:27:00 | ||
图片预览




文档简介
北师大版数学 九上 第一章 1.1菱形的现在与判定测试卷B卷
选择题(共30分)
1.如图,在 ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( )
A.OE=OF B.AE=CF C.EF⊥AC D.EF=AC
2.如图,在菱形中,对角线,分别为16和12,于点E,则( )
A. B. C.10 D.8
3.如图,在平面直角坐标系中,四边形是菱形,,点坐标为,将菱形绕原点顺时针旋转,旋转后点的坐标为( )
A. B. C. D.
4.如图,在平面直角坐标系中,点的坐标为,点的坐标为,以为边作矩形.动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A. B. C. D.
5.如图,菱形中,,,是对角线上的任意一点,则的最小值为( ).
A. B. C.2 D.
6.一个平行四边形的一条边长为7,两条对角线的长分别是10和,则这个平行四边形的面积为( )
A. B. C.35 D.
7.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,,,若AD=2,则四边形CODE的周长为( )
A.12 B.10 C.8 D.4
8.如图,在菱形中,与相交于点O,的垂直平分线分别交,于点E,F,连接,若,则的度数是( )
A.60° B.75 C.80° D.110°
9.如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
10.如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A.2 B.2 C.4 D.4
填空题(共24分)
11.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
12.已知菱形的两条对角线长分别为3cm,4cm,则它的面积是 cm2
13.如图,平行四边形ABCD中,对角线AC,BD相交于点O,且 , ,要使得四边形ABCD是菱形,应添加的条件是 (只填写一个条件).
14.中国结,象征着中华民族的历史文化与精致.小明家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形ABCD,测得,,直线交两对边与E、F,则EF的长为 cm.
15.如图,在菱形中,,.点E、F同时从A、C两点出发,分别沿,方向向点匀速移动(到点即停止).点的速度为,点的速度为,经过后恰为等边三角形,则此时的值为 .
16.如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③.其中正确的结论是 .(填写所有正确结论的序号)
解答题(共46分)
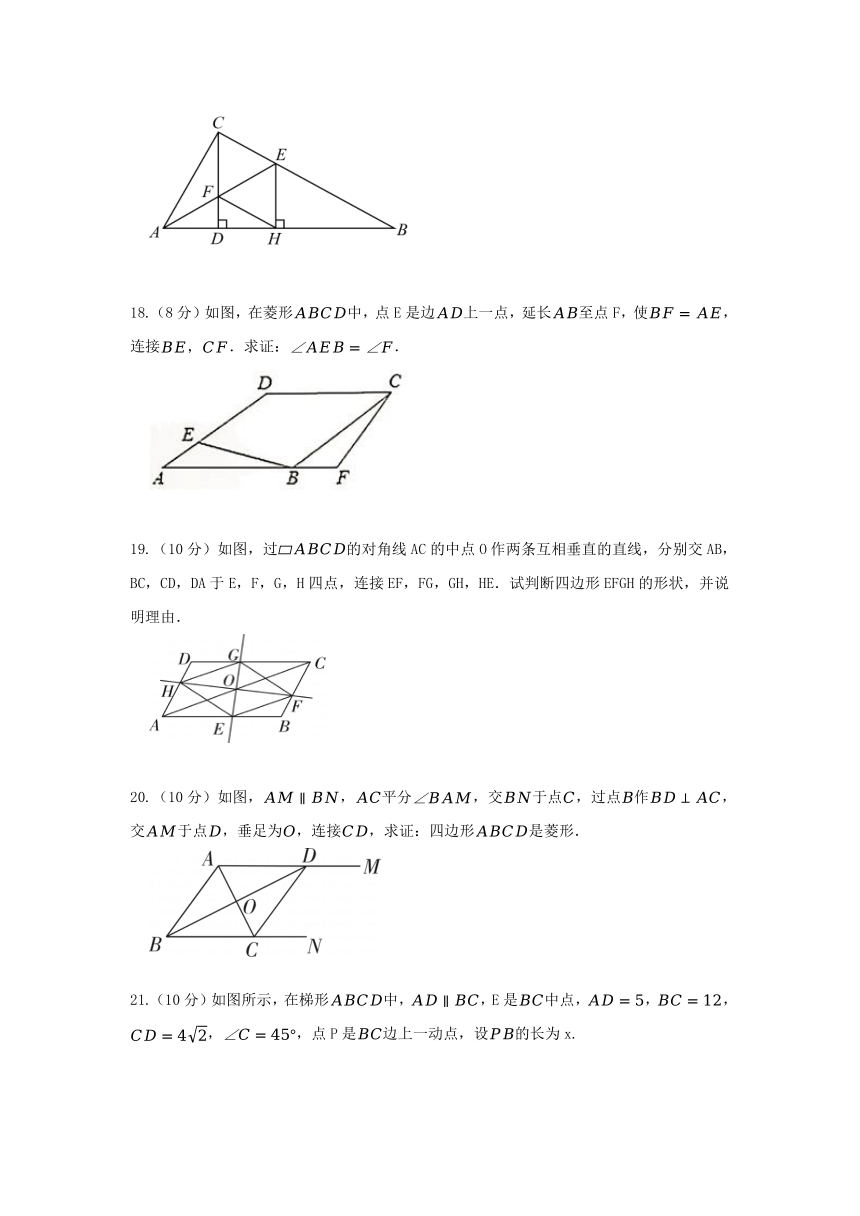
17.(8分)如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形.
18.(8分)如图,在菱形中,点E是边上一点,延长至点F,使,连接.求证:.
19.(10分)如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
20.(10分)如图,,平分,交于点,过点作,交于点,垂足为,连接,求证:四边形是菱形.
21.(10分)如图所示,在梯形中,,E是中点,,, ,,点P是边上一动点,设的长为x.
(1)当x的值为 时,以点为顶点的四边形为直角梯形;
(2)当x的值为 时,以点为顶点的四边形是平行四边形;
(3)点P在上运动的过程中,以点为顶点的四边形能否构成菱形?试说明理由.
北师大版数学 九上 第一章 1.1菱形的现在与判定测试卷B卷
选择题(共30分)
1.如图,在 ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( )
A.OE=OF B.AE=CF C.EF⊥AC D.EF=AC
【答案】C
【知识点】平行四边形的性质;菱形的判定;三角形全等的判定(AAS)
【解析】【解答】解:∵平行四边形ABCD,
∴AE∥FC,
∴∠AEO=∠CFO,
∵点O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
∴△AOE≌△COF(AAS)
∴OE=OF,
∴四边形AFCE是平行四边形,
∴当EF⊥AC时四边形AFCE是菱形.
故答案为:C
2.如图,在菱形中,对角线,分别为16和12,于点E,则( )
A. B. C.10 D.8
【答案】A
【知识点】菱形的性质
【解析】【解答】解:
∵四边形是菱形
∴且平分对角线
又∵,
∴AO=8,BO=6,
∴
∵菱形的面积等于对角线乘积的一半,等于底乘高
∴
∴
故答案为:A.
3.如图,在平面直角坐标系中,四边形是菱形,,点坐标为,将菱形绕原点顺时针旋转,旋转后点的坐标为( )
A. B. C. D.
【答案】B
【知识点】菱形的性质;旋转的性质
【解析】【解答】解:∵四边形OABC是菱形,点A坐标为(6,0),
∴OA=OC=BC=6,
又∵∠AOC=60°,
∴点C坐标为,
∴点B坐标为
绕原点O旋转180°后,点B关于原点对称,
∴旋转后点B的坐标为.
故答案为:B.
4.如图,在平面直角坐标系中,点的坐标为,点的坐标为,以为边作矩形.动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A. B. C. D.
【答案】D
【知识点】勾股定理;平行四边形的判定;菱形的判定与性质;矩形的性质
【解析】【解答】解:如图,连接AC、EF,
∵点A(9,0),点C(0,3),
∴OA=9,OC=3,
∵四边形OABC是矩形,
∴BC=OA=9,BC∥OA,∠COE=90°,
∵BF=OE=4,
∴CF=AE=9-4=5,
∴四边形AECF是平行四边形,
在Rt△OCE中,∠COE=90°,OE=4,OC=3,
∴CE=5,
∴CE=AE=5,
∴平行四边形AECF是菱形,
∴AC·EF=2AE·OC=2×5×3=30.
故答案为:D.
5.如图,菱形中,,,是对角线上的任意一点,则的最小值为( ).
A. B. C.2 D.
【答案】B
【知识点】菱形的判定与性质
【解析】【解答】如图所示:过点B作BF⊥DC,垂足为F,BF交AC与点E.
∵菱形ABCD中,AB=2,∠D=120°,
∴BC=2,∠FBC=30°,∠DCA=30°.
∴EF=EC.
∴BF=BE+EF=BE+EC
由垂线段最短可知:当BF⊥DC,时,FB有最小值,即
∴最小值=BF=BC=×4=
故答案为:B
6.一个平行四边形的一条边长为7,两条对角线的长分别是10和,则这个平行四边形的面积为( )
A. B. C.35 D.
【答案】B
【知识点】勾股定理的逆定理;平行四边形的性质;菱形的判定与性质
【解析】【解答】解:设平行四边形ABCD的对角线交于点O,且,,,
∴,,
∵,
∴,
∴,
∴平行四边形ABCD是菱形.
∴平行四边形ABCD的面积为,
故答案为:B.
7.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,,,若AD=2,则四边形CODE的周长为( )
A.12 B.10 C.8 D.4
【答案】C
【知识点】等边三角形的判定与性质;菱形的判定与性质;矩形的性质
【解析】【解答】解:因为矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,
所以OA=OD=OC=OB,∠AOD=60°,
所以△AOD是等边三角形,
所以OD=AD=2.
因为,,
所以四边形ODEC是平行四边形,
因为OD=OC,
所以四边形ODEC是菱形,
所以四边形的周长等于4OD=4AD,
因为AD=2,
所以四边形CODE的周长为8,
故答案为:C.
8.如图,在菱形中,与相交于点O,的垂直平分线分别交,于点E,F,连接,若,则的度数是( )
A.60° B.75 C.80° D.110°
【答案】B
【知识点】线段垂直平分线的性质;菱形的性质
【解析】【解答】解:连接BF,如图所示:
∵四边形ABCD是菱形,
∴∠DCF=∠BCF=∠BCD=35°,AC垂直平分BD,AD∥BC,
∴BF=DF,
∵EF是BC的垂直平分线,
∴BF=CF,
∴DF=CF,
∴∠CDF=∠DCF=35°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADC=180°-70°=110°,
∴∠ADF=110°-35°=75°,
故答案为:B.
9.如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
【答案】B
【知识点】全等三角形的判定与性质;菱形的性质;旋转的性质
【解析】【解答】解:连结对角线 , ,∴ ,
∵菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,
∴ , , 三点共线,
, , 三点共线,
∴
∴
由题目已知和菱形的性质可得:
∴
∴
∴ ,②不符合题意;
在 和 中
∴ ≌
∴
∴由 ,
∴ ≌
∴①符合题意;
∴ 为 的角平分线,
∴ (三线合一)
∴③符合题意;
∵ ,
∴
在菱形ABCD中,
∴
∴在 中,
,
∴四边形AB′ED的周长为:
=
∴④不符合题意
综上所述,正确的有①③,
故答案为:B
10.如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A.2 B.2 C.4 D.4
【答案】B
【知识点】菱形的性质;轴对称的应用-最短距离问题
【解析】【解答】解:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8 ,
∴AB=BC=4,AB CE′=8 ,
∴CE′=2 ,
在Rt△BCE′中,BE′= ,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2 ,
故答案为:B.
填空题(共24分)
11.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
【答案】24
【知识点】菱形的性质
【解析】【解答】解:∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是=24(cm2),
故答案为:24.
12.已知菱形的两条对角线长分别为3cm,4cm,则它的面积是 cm2
【答案】6
【知识点】菱形的性质
【解析】【解答】解:由已知得,菱形的面积为 .
故答案为
13.如图,平行四边形ABCD中,对角线AC,BD相交于点O,且 , ,要使得四边形ABCD是菱形,应添加的条件是 (只填写一个条件).
【答案】AB=BC(答案不唯一)
【知识点】菱形的判定
【解析】【解答】解:应添加的条件是:AB=BC,理由如下:
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形.
故答案为:AB=BC(答案不唯一).
14.中国结,象征着中华民族的历史文化与精致.小明家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形ABCD,测得,,直线交两对边与E、F,则EF的长为 cm.
【答案】
【知识点】菱形的性质
【解析】【解答】解:在菱形ABCD中,AC⊥BD,CD∥AB,
∵,,
∴ ,
∴,
设AB边的高为h,
∴菱形ABCD的面积等于,
即,解得:,
∵,
∴.
故答案为:
15.如图,在菱形中,,.点E、F同时从A、C两点出发,分别沿,方向向点匀速移动(到点即停止).点的速度为,点的速度为,经过后恰为等边三角形,则此时的值为 .
【答案】
【知识点】等边三角形的判定与性质;菱形的性质;三角形全等的判定(SAS)
【解析】【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴∠ADC=120°,AD=AB,
∴∠ADB=60°,
∴△ABD为等边三角形,
∴BD=AD.
若△DEF为等边三角形,则∠DEF=60°,DE=DF,
∴∠ADE=∠BDF.
∵AD=BD,∠ADE=∠BDF,DE=DF,
∴△ADE≌△BDF(SAS),
∴AE=BF.
∵点E的速度为2cm/s,点F的速度为4cm/s,
∴AE=2tcm,CF=4tcm,
∴BF=BC-CF=10-4t,
∴2t=10-4t,
解得t=.
故答案为:.
16.如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③
【知识点】菱形的判定;相似三角形的判定与性质;三角形全等的判定(SSS);三角形的中位线定理
【解析】【解答】解:①∵D、E、F分别为AB、BC、AC的中点,
∴DE、DF、EF为△ABC的中位线,
∴AD=AB=FE,AF=AC=FC,DF=BC=EC.
在△ADF和△FEC中,
,
∴△ADF≌△FEC(SSS),结论①正确;
②∵E、F分别为BC、AC的中点,
∴EF为△ABC的中位线,
∴EF∥AB,EF=AB=AD,
∴四边形ADEF为平行四边形.
∵AB=AC,D、F分别为AB、AC的中点,
∴AD=AF,
∴四边形ADEF为菱形,结论②正确;
③∵D、F分别为AB、AC的中点,
∴DF为△ABC的中位线,
∴DF∥BC,DF=BC,
∴△ADF∽△ABC,
∴,结论③正确.
故答案为:①②③.
解答题(共46分)
17.(8分)如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形.
【答案】证明:∵∠ACB=90°,AE平分∠BAC,EH⊥AB,
∴CE=EH,
在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,由勾股定理得:AC=AH,
∵AE平分∠CAB,
∴∠CAF=∠HAF,
在△CAF和△HAF中
∴△CAF≌△HAF(SAS),
∴∠ACD=∠AHF,
∵CD⊥AB,∠ACB=90°,
∴∠CDA=∠ACB=90°,
∴∠B+∠CAB=90°,∠CAB+∠ACD=90°,
∴∠ACD=∠B=∠AHF,
∴FH CE,
∵CD⊥AB,EH⊥AB,
∴CF EH,
∴四边形CFHE是平行四边形,
∵CE=EH,
∴四边形CFHE是菱形.
18.(8分)如图,在菱形中,点E是边上一点,延长至点F,使,连接.求证:.
【答案】证明:菱形,
,
,
在和中,
,
,
.
19.(10分)如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
【答案】解:四边形EFGH的形状是菱形,理由如下:
∵四边形为平行四边形,
∴,
∴,
在和中, ,
∴(ASA)
∴OE=OG.
同理可证OF=OH.
∵,
∴四边形为菱形.
20.(10分)如图,,平分,交于点,过点作,交于点,垂足为,连接,求证:四边形是菱形.
【答案】证明:如图,
∵AC平分∠BAM,AM∥BN,
∴,.
∴.
∴.
又∵BD⊥AC于点O,
∴.
在△AOD和△COB中,
,
∴.
∴.
∴四边形ABCD是平行四边形.
又∵BA=BC,
∴平行四边形ABCD是菱形.
21.(10分)如图所示,在梯形中,,E是中点,,, ,,点P是边上一动点,设的长为x.
(1)当x的值为 时,以点为顶点的四边形为直角梯形;
(2)当x的值为 时,以点为顶点的四边形是平行四边形;
(3)点P在上运动的过程中,以点为顶点的四边形能否构成菱形?试说明理由.
【答案】(1)3或8
(2)1或11
(3)解:点P在边上运动的过程中,以为顶点的四边形能构成菱形,
理由如下:
①当点P在点E左侧时,如下图,过点作于点H,
∵,,
∴,
∴,
∴,
在中,由勾股定理可得,
∴,
∵是的中点,,
∴,
∴,
∴在中,,
∴,
即此时以为顶点的四边形不能构成菱形;
②当点P在点E右侧时,如下图,过点D作于点H,
由(1)可知,当时,四边形为平行四边形,
此时,,
∴,
∴在中,,
∴,
∴四边形为菱形.
综上所述,点P在边上运动的过程中,以为顶点的四边形能构成菱形.
【知识点】勾股定理;菱形的判定;四边形-动点问题
【解析】【解答】解:(1)分别过A、D作于M,于N
∵
∴是矩形,
∴,
∵,,
∴,
选择题(共30分)
1.如图,在 ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( )
A.OE=OF B.AE=CF C.EF⊥AC D.EF=AC
2.如图,在菱形中,对角线,分别为16和12,于点E,则( )
A. B. C.10 D.8
3.如图,在平面直角坐标系中,四边形是菱形,,点坐标为,将菱形绕原点顺时针旋转,旋转后点的坐标为( )
A. B. C. D.
4.如图,在平面直角坐标系中,点的坐标为,点的坐标为,以为边作矩形.动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A. B. C. D.
5.如图,菱形中,,,是对角线上的任意一点,则的最小值为( ).
A. B. C.2 D.
6.一个平行四边形的一条边长为7,两条对角线的长分别是10和,则这个平行四边形的面积为( )
A. B. C.35 D.
7.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,,,若AD=2,则四边形CODE的周长为( )
A.12 B.10 C.8 D.4
8.如图,在菱形中,与相交于点O,的垂直平分线分别交,于点E,F,连接,若,则的度数是( )
A.60° B.75 C.80° D.110°
9.如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
10.如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A.2 B.2 C.4 D.4
填空题(共24分)
11.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
12.已知菱形的两条对角线长分别为3cm,4cm,则它的面积是 cm2
13.如图,平行四边形ABCD中,对角线AC,BD相交于点O,且 , ,要使得四边形ABCD是菱形,应添加的条件是 (只填写一个条件).
14.中国结,象征着中华民族的历史文化与精致.小明家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形ABCD,测得,,直线交两对边与E、F,则EF的长为 cm.
15.如图,在菱形中,,.点E、F同时从A、C两点出发,分别沿,方向向点匀速移动(到点即停止).点的速度为,点的速度为,经过后恰为等边三角形,则此时的值为 .
16.如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③.其中正确的结论是 .(填写所有正确结论的序号)
解答题(共46分)
17.(8分)如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形.
18.(8分)如图,在菱形中,点E是边上一点,延长至点F,使,连接.求证:.
19.(10分)如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
20.(10分)如图,,平分,交于点,过点作,交于点,垂足为,连接,求证:四边形是菱形.
21.(10分)如图所示,在梯形中,,E是中点,,, ,,点P是边上一动点,设的长为x.
(1)当x的值为 时,以点为顶点的四边形为直角梯形;
(2)当x的值为 时,以点为顶点的四边形是平行四边形;
(3)点P在上运动的过程中,以点为顶点的四边形能否构成菱形?试说明理由.
北师大版数学 九上 第一章 1.1菱形的现在与判定测试卷B卷
选择题(共30分)
1.如图,在 ABCD中,O为AC的中点,经过点O的直线交AD于E交BC于F,连接AF、CE,下列选项可以使四边形AFCE是菱形的为( )
A.OE=OF B.AE=CF C.EF⊥AC D.EF=AC
【答案】C
【知识点】平行四边形的性质;菱形的判定;三角形全等的判定(AAS)
【解析】【解答】解:∵平行四边形ABCD,
∴AE∥FC,
∴∠AEO=∠CFO,
∵点O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
∴△AOE≌△COF(AAS)
∴OE=OF,
∴四边形AFCE是平行四边形,
∴当EF⊥AC时四边形AFCE是菱形.
故答案为:C
2.如图,在菱形中,对角线,分别为16和12,于点E,则( )
A. B. C.10 D.8
【答案】A
【知识点】菱形的性质
【解析】【解答】解:
∵四边形是菱形
∴且平分对角线
又∵,
∴AO=8,BO=6,
∴
∵菱形的面积等于对角线乘积的一半,等于底乘高
∴
∴
故答案为:A.
3.如图,在平面直角坐标系中,四边形是菱形,,点坐标为,将菱形绕原点顺时针旋转,旋转后点的坐标为( )
A. B. C. D.
【答案】B
【知识点】菱形的性质;旋转的性质
【解析】【解答】解:∵四边形OABC是菱形,点A坐标为(6,0),
∴OA=OC=BC=6,
又∵∠AOC=60°,
∴点C坐标为,
∴点B坐标为
绕原点O旋转180°后,点B关于原点对称,
∴旋转后点B的坐标为.
故答案为:B.
4.如图,在平面直角坐标系中,点的坐标为,点的坐标为,以为边作矩形.动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
A. B. C. D.
【答案】D
【知识点】勾股定理;平行四边形的判定;菱形的判定与性质;矩形的性质
【解析】【解答】解:如图,连接AC、EF,
∵点A(9,0),点C(0,3),
∴OA=9,OC=3,
∵四边形OABC是矩形,
∴BC=OA=9,BC∥OA,∠COE=90°,
∵BF=OE=4,
∴CF=AE=9-4=5,
∴四边形AECF是平行四边形,
在Rt△OCE中,∠COE=90°,OE=4,OC=3,
∴CE=5,
∴CE=AE=5,
∴平行四边形AECF是菱形,
∴AC·EF=2AE·OC=2×5×3=30.
故答案为:D.
5.如图,菱形中,,,是对角线上的任意一点,则的最小值为( ).
A. B. C.2 D.
【答案】B
【知识点】菱形的判定与性质
【解析】【解答】如图所示:过点B作BF⊥DC,垂足为F,BF交AC与点E.
∵菱形ABCD中,AB=2,∠D=120°,
∴BC=2,∠FBC=30°,∠DCA=30°.
∴EF=EC.
∴BF=BE+EF=BE+EC
由垂线段最短可知:当BF⊥DC,时,FB有最小值,即
∴最小值=BF=BC=×4=
故答案为:B
6.一个平行四边形的一条边长为7,两条对角线的长分别是10和,则这个平行四边形的面积为( )
A. B. C.35 D.
【答案】B
【知识点】勾股定理的逆定理;平行四边形的性质;菱形的判定与性质
【解析】【解答】解:设平行四边形ABCD的对角线交于点O,且,,,
∴,,
∵,
∴,
∴,
∴平行四边形ABCD是菱形.
∴平行四边形ABCD的面积为,
故答案为:B.
7.如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,,,若AD=2,则四边形CODE的周长为( )
A.12 B.10 C.8 D.4
【答案】C
【知识点】等边三角形的判定与性质;菱形的判定与性质;矩形的性质
【解析】【解答】解:因为矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,
所以OA=OD=OC=OB,∠AOD=60°,
所以△AOD是等边三角形,
所以OD=AD=2.
因为,,
所以四边形ODEC是平行四边形,
因为OD=OC,
所以四边形ODEC是菱形,
所以四边形的周长等于4OD=4AD,
因为AD=2,
所以四边形CODE的周长为8,
故答案为:C.
8.如图,在菱形中,与相交于点O,的垂直平分线分别交,于点E,F,连接,若,则的度数是( )
A.60° B.75 C.80° D.110°
【答案】B
【知识点】线段垂直平分线的性质;菱形的性质
【解析】【解答】解:连接BF,如图所示:
∵四边形ABCD是菱形,
∴∠DCF=∠BCF=∠BCD=35°,AC垂直平分BD,AD∥BC,
∴BF=DF,
∵EF是BC的垂直平分线,
∴BF=CF,
∴DF=CF,
∴∠CDF=∠DCF=35°,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADC=180°-70°=110°,
∴∠ADF=110°-35°=75°,
故答案为:B.
9.如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
【答案】B
【知识点】全等三角形的判定与性质;菱形的性质;旋转的性质
【解析】【解答】解:连结对角线 , ,∴ ,
∵菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,
∴ , , 三点共线,
, , 三点共线,
∴
∴
由题目已知和菱形的性质可得:
∴
∴
∴ ,②不符合题意;
在 和 中
∴ ≌
∴
∴由 ,
∴ ≌
∴①符合题意;
∴ 为 的角平分线,
∴ (三线合一)
∴③符合题意;
∵ ,
∴
在菱形ABCD中,
∴
∴在 中,
,
∴四边形AB′ED的周长为:
=
∴④不符合题意
综上所述,正确的有①③,
故答案为:B
10.如图,已知菱形ABCD的周长为16,面积为 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A.2 B.2 C.4 D.4
【答案】B
【知识点】菱形的性质;轴对称的应用-最短距离问题
【解析】【解答】解:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8 ,
∴AB=BC=4,AB CE′=8 ,
∴CE′=2 ,
在Rt△BCE′中,BE′= ,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2 ,
故答案为:B.
填空题(共24分)
11.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
【答案】24
【知识点】菱形的性质
【解析】【解答】解:∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是=24(cm2),
故答案为:24.
12.已知菱形的两条对角线长分别为3cm,4cm,则它的面积是 cm2
【答案】6
【知识点】菱形的性质
【解析】【解答】解:由已知得,菱形的面积为 .
故答案为
13.如图,平行四边形ABCD中,对角线AC,BD相交于点O,且 , ,要使得四边形ABCD是菱形,应添加的条件是 (只填写一个条件).
【答案】AB=BC(答案不唯一)
【知识点】菱形的判定
【解析】【解答】解:应添加的条件是:AB=BC,理由如下:
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形.
故答案为:AB=BC(答案不唯一).
14.中国结,象征着中华民族的历史文化与精致.小明家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形ABCD,测得,,直线交两对边与E、F,则EF的长为 cm.
【答案】
【知识点】菱形的性质
【解析】【解答】解:在菱形ABCD中,AC⊥BD,CD∥AB,
∵,,
∴ ,
∴,
设AB边的高为h,
∴菱形ABCD的面积等于,
即,解得:,
∵,
∴.
故答案为:
15.如图,在菱形中,,.点E、F同时从A、C两点出发,分别沿,方向向点匀速移动(到点即停止).点的速度为,点的速度为,经过后恰为等边三角形,则此时的值为 .
【答案】
【知识点】等边三角形的判定与性质;菱形的性质;三角形全等的判定(SAS)
【解析】【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴∠ADC=120°,AD=AB,
∴∠ADB=60°,
∴△ABD为等边三角形,
∴BD=AD.
若△DEF为等边三角形,则∠DEF=60°,DE=DF,
∴∠ADE=∠BDF.
∵AD=BD,∠ADE=∠BDF,DE=DF,
∴△ADE≌△BDF(SAS),
∴AE=BF.
∵点E的速度为2cm/s,点F的速度为4cm/s,
∴AE=2tcm,CF=4tcm,
∴BF=BC-CF=10-4t,
∴2t=10-4t,
解得t=.
故答案为:.
16.如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③
【知识点】菱形的判定;相似三角形的判定与性质;三角形全等的判定(SSS);三角形的中位线定理
【解析】【解答】解:①∵D、E、F分别为AB、BC、AC的中点,
∴DE、DF、EF为△ABC的中位线,
∴AD=AB=FE,AF=AC=FC,DF=BC=EC.
在△ADF和△FEC中,
,
∴△ADF≌△FEC(SSS),结论①正确;
②∵E、F分别为BC、AC的中点,
∴EF为△ABC的中位线,
∴EF∥AB,EF=AB=AD,
∴四边形ADEF为平行四边形.
∵AB=AC,D、F分别为AB、AC的中点,
∴AD=AF,
∴四边形ADEF为菱形,结论②正确;
③∵D、F分别为AB、AC的中点,
∴DF为△ABC的中位线,
∴DF∥BC,DF=BC,
∴△ADF∽△ABC,
∴,结论③正确.
故答案为:①②③.
解答题(共46分)
17.(8分)如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形.
【答案】证明:∵∠ACB=90°,AE平分∠BAC,EH⊥AB,
∴CE=EH,
在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,由勾股定理得:AC=AH,
∵AE平分∠CAB,
∴∠CAF=∠HAF,
在△CAF和△HAF中
∴△CAF≌△HAF(SAS),
∴∠ACD=∠AHF,
∵CD⊥AB,∠ACB=90°,
∴∠CDA=∠ACB=90°,
∴∠B+∠CAB=90°,∠CAB+∠ACD=90°,
∴∠ACD=∠B=∠AHF,
∴FH CE,
∵CD⊥AB,EH⊥AB,
∴CF EH,
∴四边形CFHE是平行四边形,
∵CE=EH,
∴四边形CFHE是菱形.
18.(8分)如图,在菱形中,点E是边上一点,延长至点F,使,连接.求证:.
【答案】证明:菱形,
,
,
在和中,
,
,
.
19.(10分)如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
【答案】解:四边形EFGH的形状是菱形,理由如下:
∵四边形为平行四边形,
∴,
∴,
在和中, ,
∴(ASA)
∴OE=OG.
同理可证OF=OH.
∵,
∴四边形为菱形.
20.(10分)如图,,平分,交于点,过点作,交于点,垂足为,连接,求证:四边形是菱形.
【答案】证明:如图,
∵AC平分∠BAM,AM∥BN,
∴,.
∴.
∴.
又∵BD⊥AC于点O,
∴.
在△AOD和△COB中,
,
∴.
∴.
∴四边形ABCD是平行四边形.
又∵BA=BC,
∴平行四边形ABCD是菱形.
21.(10分)如图所示,在梯形中,,E是中点,,, ,,点P是边上一动点,设的长为x.
(1)当x的值为 时,以点为顶点的四边形为直角梯形;
(2)当x的值为 时,以点为顶点的四边形是平行四边形;
(3)点P在上运动的过程中,以点为顶点的四边形能否构成菱形?试说明理由.
【答案】(1)3或8
(2)1或11
(3)解:点P在边上运动的过程中,以为顶点的四边形能构成菱形,
理由如下:
①当点P在点E左侧时,如下图,过点作于点H,
∵,,
∴,
∴,
∴,
在中,由勾股定理可得,
∴,
∵是的中点,,
∴,
∴,
∴在中,,
∴,
即此时以为顶点的四边形不能构成菱形;
②当点P在点E右侧时,如下图,过点D作于点H,
由(1)可知,当时,四边形为平行四边形,
此时,,
∴,
∴在中,,
∴,
∴四边形为菱形.
综上所述,点P在边上运动的过程中,以为顶点的四边形能构成菱形.
【知识点】勾股定理;菱形的判定;四边形-动点问题
【解析】【解答】解:(1)分别过A、D作于M,于N
∵
∴是矩形,
∴,
∵,,
∴,
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
