14.2.1平方差公式 课件
文档属性
| 名称 | 14.2.1平方差公式 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 912.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-21 15:59:42 | ||
图片预览






文档简介
课件26张PPT。平方差公式开门见山、探究新知 计算下列多项式的积,你能发现什么规律?4x2 - y2(a+b)(a-b) = a2-b2
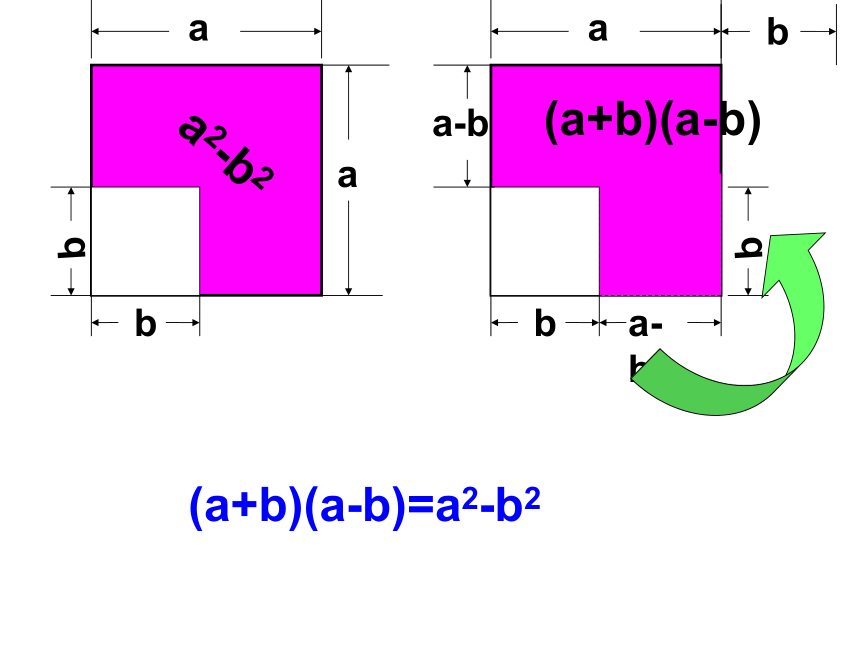
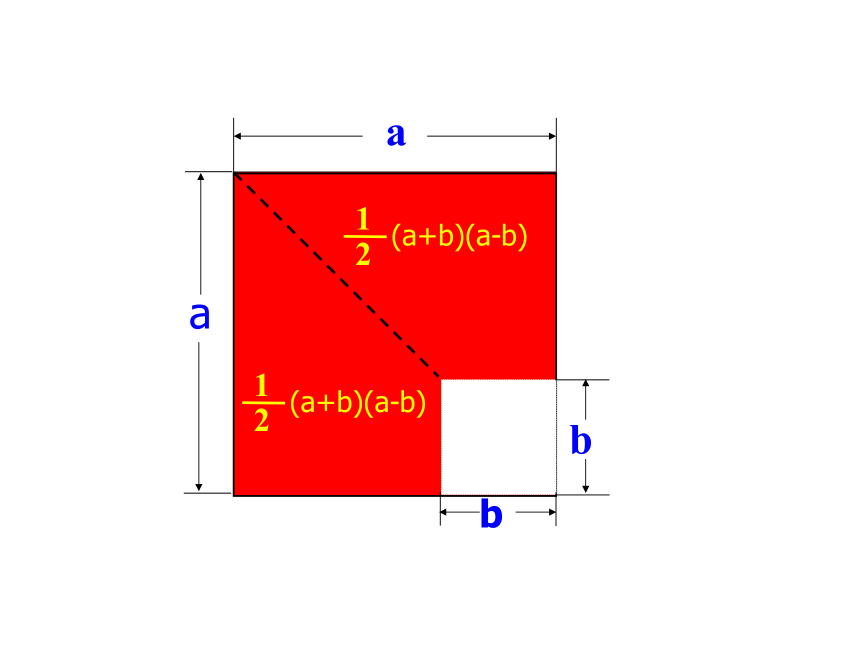
(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2b2猜想:验证你还能用其它方法证明此结论的正确性吗?规律探索:a2-b2(a+b)(a-b)(a+b)(a-b)=a2-b2babbab(a+b)(a-b)
=a2-b2运用数形结合的数学思想(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。(a+b)(a-b)=a2-b2
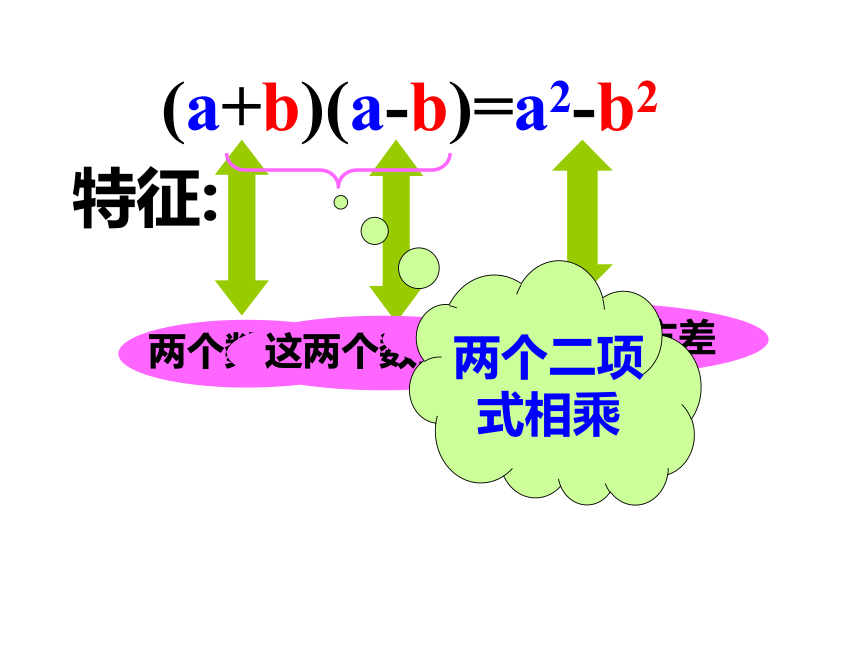
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
说明: 公式中的a,b可以表示
一个单项式也可以表示一个多项式.小试牛刀、巩固应用你能在下列式子中找出与公式“a”“b”对应的项吗?用公式关键是识别两数
完全相同项 a
互为相反数项 b小试牛刀、巩固应用我们再看看( + )( 2a-b )这一式子还能用这公式计算吗?b2a小试牛刀、巩固应用将式子变为(b-2a)(2a-b),还可以用这个公式吗?( + )( 2a-b )b2a(b+2a)(2a-b)(b-2a)(-2a-b)(-b-2a)(2a-b)(b-2a)(2a+b)=(2a ) 2 -b2=(-2a ) 2 -b2=(-b ) 2 -(2a)2=(b ) 2 -(2a)2我们再看看( + )( 2a-b )这一式子还能用这公式计算吗?b2a快乐游戏、巩固识别 下列式子中,哪两个式子相乘能运用“平方差公式” 进行计算.① ②③④ ⑤⑥(y+2)(3x-2)(-3+2a)(-y+2)(-3-2a)(-3x+2)认真改错、有所提高 下列各式的计算对不对?若不对应当怎样改正? (1) (x+4) (x-4)= x2-4;
(2) (-3n-2)(3n-2) = 9n2-4.= x2-16= 4-9n2填空 运用平方差公式计算:a2 - 9b24a2 - 9灵活应变、能力提升(1) 102×98;认真观察式子,写出解题过程.思考: (2a–b+1)(2a–b-1).(2) (y+2)(y–2) –(y–1)(y+5);灵活应变、能力提升小小归纳、认知提高 通过以上几个题目的练习,你能总结一下解这类题目时要注意什么吗?先观察式子的结构是否符合公式的结构;正确确定公式中的“a”、“b”;套用公式直接写结果.我能行!运用平方差公式计算:1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2y2-x24a2-b2x4-y42499(a+b)(a-b)=a2-b2
灵活运用平方差公式计算:变式延伸1、(3x+4)(3x-4) – (2x+3)(3x-2);
2、(x+y)(x-y)(x2+y2);
挑战极限(2+1)(22+1)(24+1)解:原式 = (2-1)(2+1)(22+1)(24+1) = (22-1)(22+1)(24+1)= (24-1)(24+1)= 28-1… (22n+1)… (22n+1)… (22n+1)… (22n+1)( )… (22n+1)= (22n-1) (22n+1)= 24n-1变式归纳小结、认知升华 (1) 今天,我们学习了什么知识?
(2) 运用公式时应注意什么?谢谢 再见
(a+b)(a-b)= a2-ab+ab-b2-ab+ab= a2-b2a2b2猜想:验证你还能用其它方法证明此结论的正确性吗?规律探索:a2-b2(a+b)(a-b)(a+b)(a-b)=a2-b2babbab(a+b)(a-b)
=a2-b2运用数形结合的数学思想(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
特征:(a+b)(a-b)=a2-b2
说明: 公式中的a,b可以表示
一个单项式也可以表示一个多项式.小试牛刀、巩固应用你能在下列式子中找出与公式“a”“b”对应的项吗?用公式关键是识别两数
完全相同项 a
互为相反数项 b小试牛刀、巩固应用我们再看看( + )( 2a-b )这一式子还能用这公式计算吗?b2a小试牛刀、巩固应用将式子变为(b-2a)(2a-b),还可以用这个公式吗?( + )( 2a-b )b2a(b+2a)(2a-b)(b-2a)(-2a-b)(-b-2a)(2a-b)(b-2a)(2a+b)=(2a ) 2 -b2=(-2a ) 2 -b2=(-b ) 2 -(2a)2=(b ) 2 -(2a)2我们再看看( + )( 2a-b )这一式子还能用这公式计算吗?b2a快乐游戏、巩固识别 下列式子中,哪两个式子相乘能运用“平方差公式” 进行计算.① ②③④ ⑤⑥(y+2)(3x-2)(-3+2a)(-y+2)(-3-2a)(-3x+2)认真改错、有所提高 下列各式的计算对不对?若不对应当怎样改正? (1) (x+4) (x-4)= x2-4;
(2) (-3n-2)(3n-2) = 9n2-4.= x2-16= 4-9n2填空 运用平方差公式计算:a2 - 9b24a2 - 9灵活应变、能力提升(1) 102×98;认真观察式子,写出解题过程.思考: (2a–b+1)(2a–b-1).(2) (y+2)(y–2) –(y–1)(y+5);灵活应变、能力提升小小归纳、认知提高 通过以上几个题目的练习,你能总结一下解这类题目时要注意什么吗?先观察式子的结构是否符合公式的结构;正确确定公式中的“a”、“b”;套用公式直接写结果.我能行!运用平方差公式计算:1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2y2-x24a2-b2x4-y42499(a+b)(a-b)=a2-b2
灵活运用平方差公式计算:变式延伸1、(3x+4)(3x-4) – (2x+3)(3x-2);
2、(x+y)(x-y)(x2+y2);
挑战极限(2+1)(22+1)(24+1)解:原式 = (2-1)(2+1)(22+1)(24+1) = (22-1)(22+1)(24+1)= (24-1)(24+1)= 28-1… (22n+1)… (22n+1)… (22n+1)… (22n+1)( )… (22n+1)= (22n-1) (22n+1)= 24n-1变式归纳小结、认知升华 (1) 今天,我们学习了什么知识?
(2) 运用公式时应注意什么?谢谢 再见
