垂直于弦的直径[上学期]

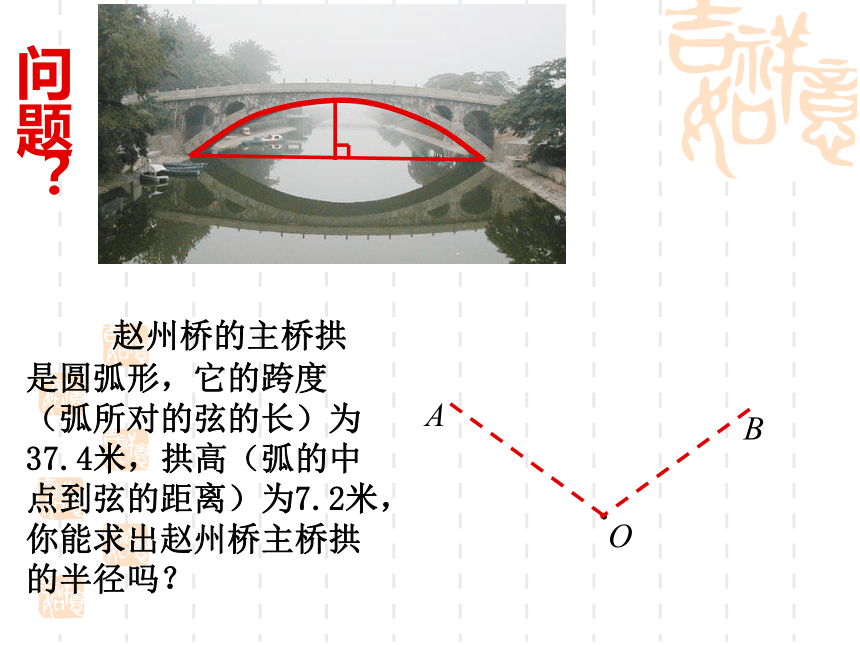
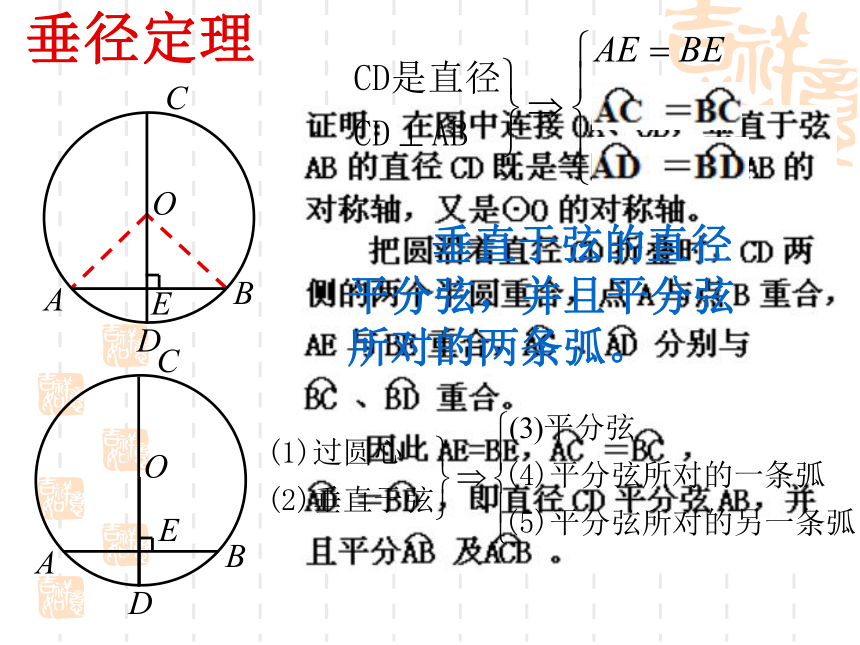
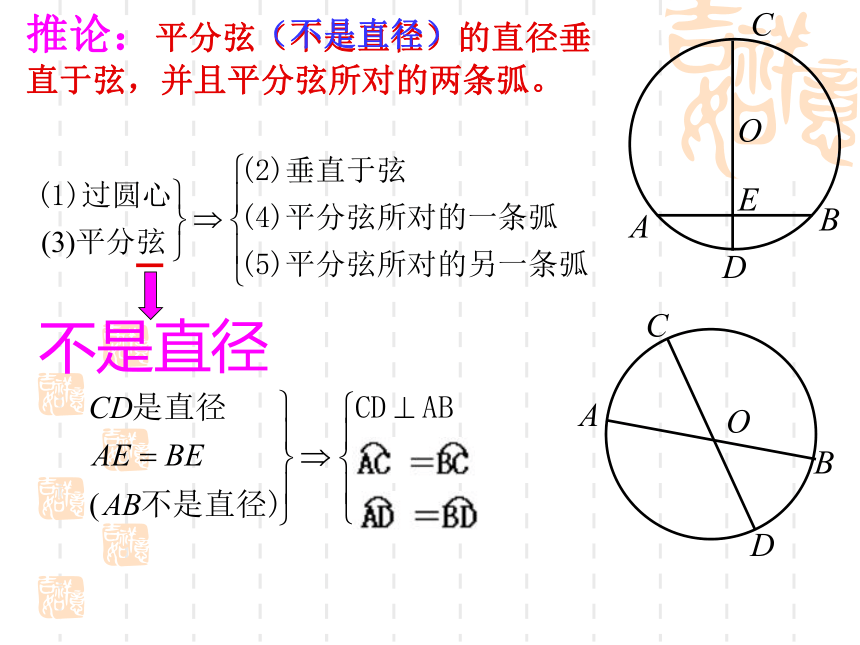
课件11张PPT。 赵州桥的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4米，拱高（弧的中点到弦的距离）为7.2米，你能求出赵州桥主桥拱的半径吗？问题？OAB 圆是轴对称图形，任何一条直径所在直线都是它的对称轴。 垂直于弦的直径平分弦，并且平分弦所对的两条弧。垂径定理BAOCDEBAOCDE不是直径 推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。 BAOCDE（不是直径）应用：已知如图，在 中，弦AB的长为8cm，若圆心O到AB的距离为3 cm，则 的半径为 cm.
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 5 赵州桥的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4米，拱高（弧的中点到弦的距离）为7.2米，你能求出赵州桥主桥拱的半径吗？问题？OABr应用：因此,赵州桥的主桥拱半径约为27.9m.1、同心圆O中，大圆的直径AB交小圆于点C、D，请问AC=BD吗？
2、如果把AB向下平移，弦AB仍然交小圆于点C、D，此时图中还有哪些相等的线段？为什么？应用：若两圆半径分别为5cm和 ，弦AB=8cm,
则AC= cm. 1在圆中研究有关弦的问题时，常过圆心作垂直于弦的垂线段，利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算. 归纳小结你学习了哪些内容？
你有哪些收获？
你掌握了哪些思想方法？
你还有什么问题 ？作业：研究性学习