垂直于弦的直径[上学期]
文档属性
| 名称 | 垂直于弦的直径[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 256.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-27 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
回顾 思考
C
B
A
D
O
(1) 圆上任意两点间的部分叫做圆弧,简称弧,连接圆上任意两点的线段叫弦,经过圆心的弦叫做直径.如图,以A、B为端点的弧记作AB,读作“圆弧AB”或“弧AB”;线段AB是⊙O的一条弦,弦CD是⊙O的一条直径.
⌒
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
如图,以A、B为端点的优弧,记作ACB;以A、B为端点的劣弧,记作AB.
︵
⌒
注意:直径是弦,但弦不一定是直径,半圆是弧,但弧不一定是半圆,半圆既不是劣弧,也不是优弧.
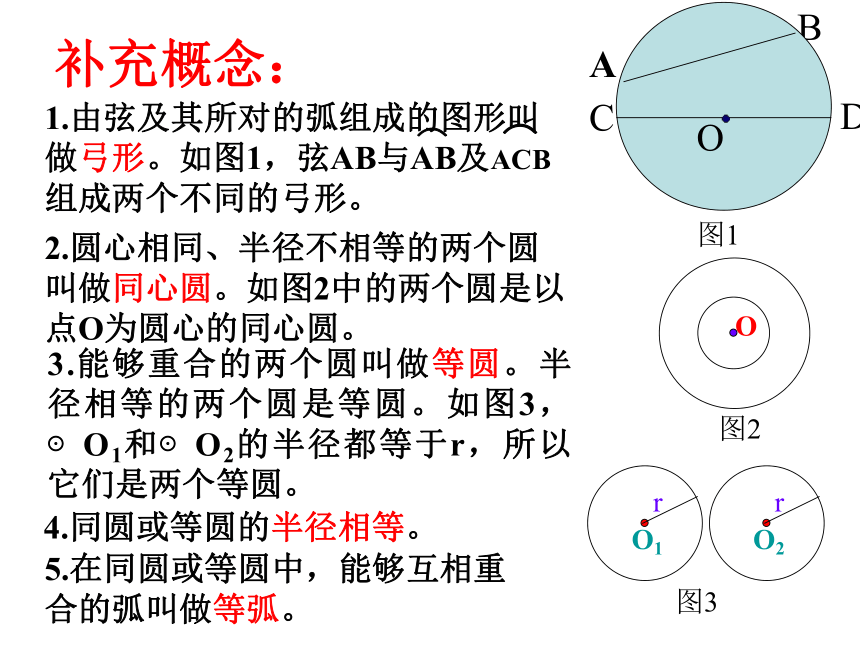
补充概念:
1.由弦及其所对的弧组成的图形叫做弓形。如图1,弦AB与AB及ACB组成两个不同的弓形。
⌒
⌒
C
B
A
D
O
图1
2.圆心相同、半径不相等的两个圆叫做同心圆。如图2中的两个圆是以点O为圆心的同心圆。
O
图2
3.能够重合的两个圆叫做等圆。半径相等的两个圆是等圆。如图3,⊙O1和⊙O2的半径都等于r,所以它们是两个等圆。
O1
r
O2
r
图3
4.同圆或等圆的半径相等。
5.在同圆或等圆中,能够互相重合的弧叫做等弧。
赵州桥又名安济桥,建于隋大业(公元605-618)年间,距今已1400年,是著名匠师李春建造。主桥拱是圆弧形,跨度(弧所对的弦)长37.4米,
拱高(弧的中点
到弦的距离)为
7.2m,是当今世
界上跨度最大、
建造最早的单孔
敞肩型石拱桥。
你能求出赵州桥
主桥拱的半径
吗?
想一想:
(1)圆是轴对称图形吗 如果是,它的对称轴是什么 你能找到多少条对称轴
(2)你是用什么方法解决上述问题的 与同伴进行交流.
圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
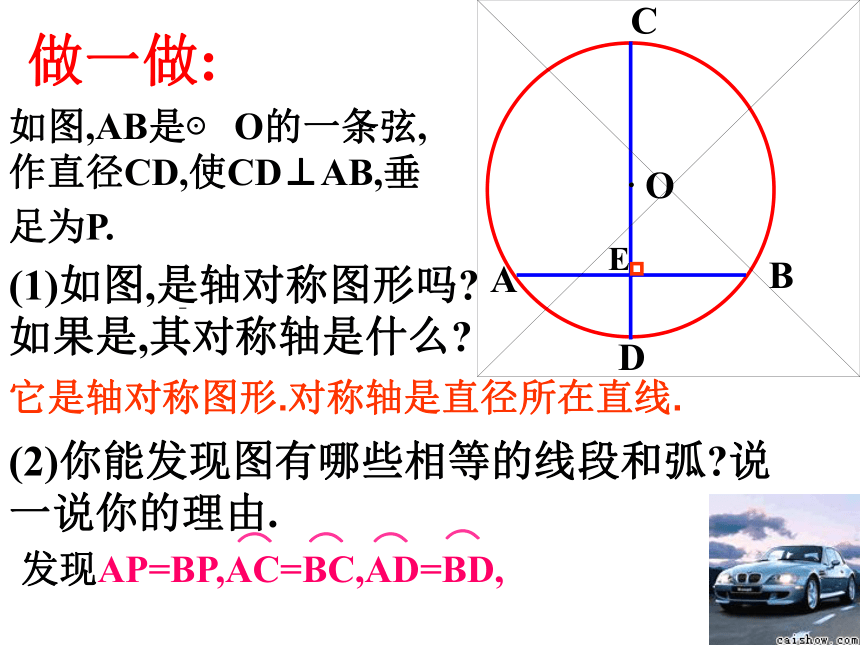
做一做:
·
A
B
C
D
O
如图,AB是⊙ O的一条弦, 作直径CD,使CD⊥AB,垂 足为P.
(1)如图,是轴对称图形吗 如果是,其对称轴是什么
(2)你能发现图有哪些相等的线段和弧 说一说你的理由.
E
它是轴对称图形.对称轴是直径所在直线.
发现AP=BP,AC=BC,AD=BD,
⌒
⌒
⌒
⌒
·
A
B
C
D
O
P
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
证明:
连结OA、OB,则OA=OB。
∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴,又是⊙O的对称轴。
∴当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AP和BP重合,AC、AD分别和BC、BD重合。
⌒
⌒
⌒
⌒
因此:
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
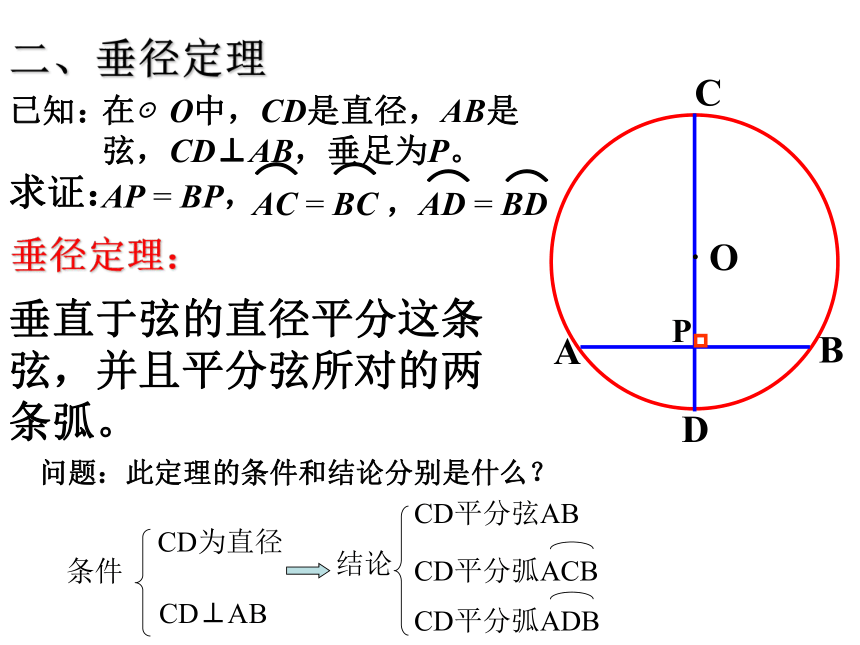
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
垂径定理:
二、垂径定理
·
A
B
C
D
O
P
问题:此定理的条件和结论分别是什么?
条件
CD为直径
CD⊥AB
CD平分弧ADB
CD平分弦AB
CD平分弧ACB
结论
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
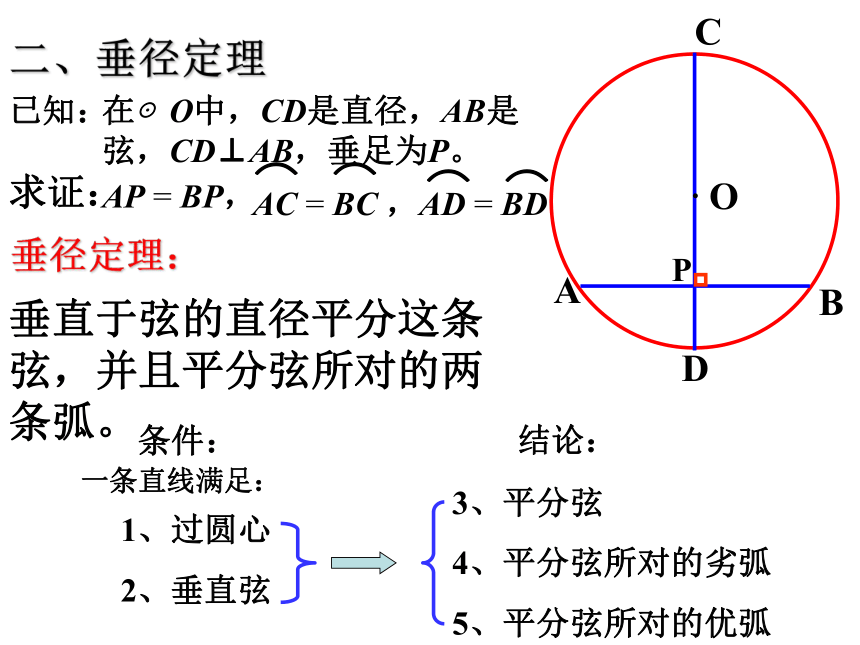
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
垂径定理:
二、垂径定理
·
A
B
C
D
O
P
条件:
结论:
一条直线满足:
1、过圆心
2、垂直弦
3、平分弦
4、平分弦所对的劣弧
5、平分弦所对的优弧
不是直径
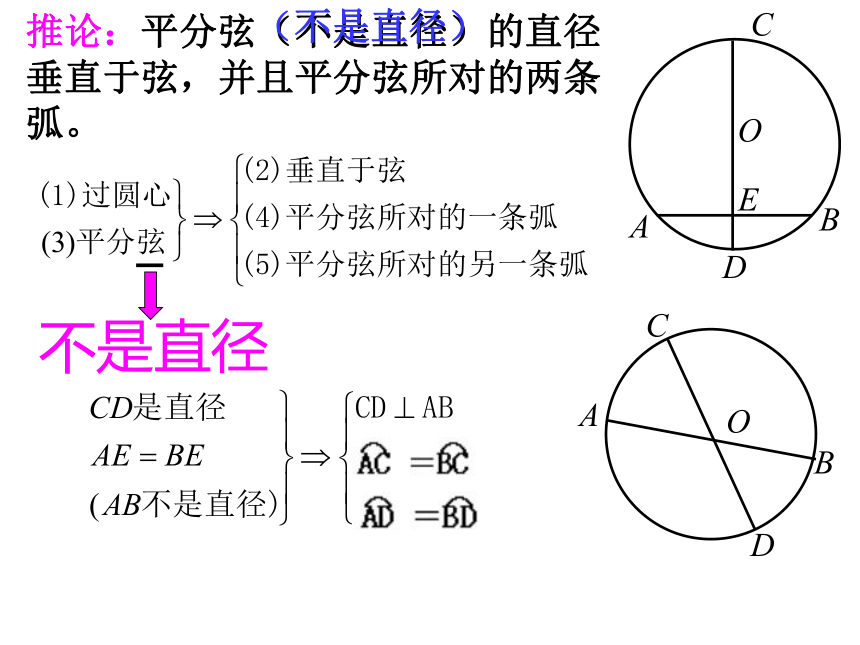
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
B
A
O
C
D
E
A
C
B
D
O
(不是直径)
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
解:连结OA。过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
∵AB=8厘米 ,∴AE=4厘米
在Rt△AOE中,
根据勾股定理有OA=5厘米
∴⊙O的半径为5厘米。
.
A
E
B
O
讲解
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
B
A
O
C
D
1、同心圆O中,大圆的直径AB交小圆于点C、D,请问AC=BD吗?
2、如果把AB向下平移,弦AB仍然交小圆于点C、D,此时图中还有哪些相等的线段?为什么?
应用:
B
A
O
C
D
E
若两圆半径分别为5cm和 ,弦AB=8cm,
则AC= cm.
1
在圆中研究有关弦的问题时,常过圆心作垂直于弦的垂线段,利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算.
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
D
C
r
应用:
O
A
B
D
C
r
如图用 表示主桥拱,设 所在圆的圆心为O,半径为r.
经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,根据前面的结论,D是AB的中点,C是 的中点,CD就是拱高.
在图中,
因此,赵州桥的主桥拱半径约为27.9m.
C
O
D
E
F
实际应用:例2.如图,一条公路的转弯处是一段圆弧(即图中CD,点O是CD的圆心),其中CD=600m,E为CD上一点, 且OE⊥ CD, 垂足为F,EF=90m.求这段弯路的半径.
⌒
⌒
⌒
解:连接OC. 设弯路的半径为Rm,则OF=(R-90)m. ∵OE⊥CD
∴CF=-CD=-×600=300 (m)
由勾股定理,得 OC2= CF2 +OF2
R2 =3002 +(R-90 )2 解这个方程,得 R=545. 所以,这段弯路的半径为545m.
1
2
1
2
耐心填一填:
如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________.
·
M
O
A
B
N
C
2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 10
3. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.
AC=BC
A
C
⌒
⌒
AN=BN
⌒
⌒
AM=BM
⌒
⌒
0<x≤6
2或8
·
M
N
O
A
B
图2
图1
C
反思:在⊙ O中,若⊙ O的半径r、
圆心到弦的距离d、弦长a中,
任意知道两个量,可根据 定理求出第三个量:
1:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。
D
C
E
O
A
B
垂径
试一试:
解:连接OA,设⊙O的半径为Rcm,则 OA=Rcm, OD=R-CD=(R-2)cm, ∵CE为⊙O的直径, 且CD⊥AB ∴AD=AB/2=8/2=4cm 在Rt△AOD中, AO2 =AD2 +OD2 即 R2 =42 +(R-2)2 解这个方程,得 R=3 即半径OC的长为3cm.
C
D
B
A
O
r
d
a
探索:如图,AB是圆O的直径,CD为弦,AE⊥CD于点E, BF⊥CD于点F, EC和DF相等吗 说明理由.
A
C
E
O
B
M
D
F
解: EC=DF
理由是: 过点O作OM⊥ EF于M,由垂径定理得 CM=DM
∵AE⊥EF, OM⊥EF, BF⊥EF
∴ AE∥OM∥BF
∵ AO=BO
∴ EM=FM
∴ EM-CM=FM-DM
即EC=DF
一变:如图,若直线EF平移到与直径AB相交于点P ( 点 P不与点A、B重合),在其它条件不变下,原结论是否改变 为什么
·
C
A
B
D
O
M
F
E
2.已知:如图,在⊙O中,AB、AC为互相垂直的两条相等的弦,OD⊥AB,OE⊥AC,D、E为垂足。求证:ADOE为正方形。
O
A
B
C
D
E
课后练习
1. 在半径为50mm的⊙O中,有长50mm的弦AB。计算:
(1) 点O与AB的距离;
(2)∠AOB的度数。
O
A
B
小结:
3.方法:(1)垂径定理和勾股定理有机结合计算弦长、半径、弦心距等问题的方法,构造直角三角形; (2)解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
A
B
O
1.“垂直于弦的直径”是圆的重要性
质之一,也是全章的基础之一,
在整章中占有举足轻重的地位是今
后研究圆与其他图形位置关系和数量关系的基础,这些知识在日常生活和生产中有广泛的应用,由于垂径及推论反映了圆的重要性质,是证明线段相等、角相等、垂直关系的重要依据,因此,它是整节书的重点.
2.本课知识点:(1)圆的轴对称性;(2)垂径定理及应用.
回顾 思考
C
B
A
D
O
(1) 圆上任意两点间的部分叫做圆弧,简称弧,连接圆上任意两点的线段叫弦,经过圆心的弦叫做直径.如图,以A、B为端点的弧记作AB,读作“圆弧AB”或“弧AB”;线段AB是⊙O的一条弦,弦CD是⊙O的一条直径.
⌒
大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧.
如图,以A、B为端点的优弧,记作ACB;以A、B为端点的劣弧,记作AB.
︵
⌒
注意:直径是弦,但弦不一定是直径,半圆是弧,但弧不一定是半圆,半圆既不是劣弧,也不是优弧.
补充概念:
1.由弦及其所对的弧组成的图形叫做弓形。如图1,弦AB与AB及ACB组成两个不同的弓形。
⌒
⌒
C
B
A
D
O
图1
2.圆心相同、半径不相等的两个圆叫做同心圆。如图2中的两个圆是以点O为圆心的同心圆。
O
图2
3.能够重合的两个圆叫做等圆。半径相等的两个圆是等圆。如图3,⊙O1和⊙O2的半径都等于r,所以它们是两个等圆。
O1
r
O2
r
图3
4.同圆或等圆的半径相等。
5.在同圆或等圆中,能够互相重合的弧叫做等弧。
赵州桥又名安济桥,建于隋大业(公元605-618)年间,距今已1400年,是著名匠师李春建造。主桥拱是圆弧形,跨度(弧所对的弦)长37.4米,
拱高(弧的中点
到弦的距离)为
7.2m,是当今世
界上跨度最大、
建造最早的单孔
敞肩型石拱桥。
你能求出赵州桥
主桥拱的半径
吗?
想一想:
(1)圆是轴对称图形吗 如果是,它的对称轴是什么 你能找到多少条对称轴
(2)你是用什么方法解决上述问题的 与同伴进行交流.
圆是轴对称图形,任何一条直径所在直线都是它的对称轴。
做一做:
·
A
B
C
D
O
如图,AB是⊙ O的一条弦, 作直径CD,使CD⊥AB,垂 足为P.
(1)如图,是轴对称图形吗 如果是,其对称轴是什么
(2)你能发现图有哪些相等的线段和弧 说一说你的理由.
E
它是轴对称图形.对称轴是直径所在直线.
发现AP=BP,AC=BC,AD=BD,
⌒
⌒
⌒
⌒
·
A
B
C
D
O
P
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
证明:
连结OA、OB,则OA=OB。
∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴,又是⊙O的对称轴。
∴当把圆沿着直径CD折叠时,CD两侧的两个半圆重合,A点和B点重合,AP和BP重合,AC、AD分别和BC、BD重合。
⌒
⌒
⌒
⌒
因此:
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
垂径定理:
二、垂径定理
·
A
B
C
D
O
P
问题:此定理的条件和结论分别是什么?
条件
CD为直径
CD⊥AB
CD平分弧ADB
CD平分弦AB
CD平分弧ACB
结论
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
垂径定理:
二、垂径定理
·
A
B
C
D
O
P
条件:
结论:
一条直线满足:
1、过圆心
2、垂直弦
3、平分弦
4、平分弦所对的劣弧
5、平分弦所对的优弧
不是直径
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
B
A
O
C
D
E
A
C
B
D
O
(不是直径)
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
解:连结OA。过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
∵AB=8厘米 ,∴AE=4厘米
在Rt△AOE中,
根据勾股定理有OA=5厘米
∴⊙O的半径为5厘米。
.
A
E
B
O
讲解
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
B
A
O
C
D
1、同心圆O中,大圆的直径AB交小圆于点C、D,请问AC=BD吗?
2、如果把AB向下平移,弦AB仍然交小圆于点C、D,此时图中还有哪些相等的线段?为什么?
应用:
B
A
O
C
D
E
若两圆半径分别为5cm和 ,弦AB=8cm,
则AC= cm.
1
在圆中研究有关弦的问题时,常过圆心作垂直于弦的垂线段,利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算.
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?
问题?
O
A
B
D
C
r
应用:
O
A
B
D
C
r
如图用 表示主桥拱,设 所在圆的圆心为O,半径为r.
经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,根据前面的结论,D是AB的中点,C是 的中点,CD就是拱高.
在图中,
因此,赵州桥的主桥拱半径约为27.9m.
C
O
D
E
F
实际应用:例2.如图,一条公路的转弯处是一段圆弧(即图中CD,点O是CD的圆心),其中CD=600m,E为CD上一点, 且OE⊥ CD, 垂足为F,EF=90m.求这段弯路的半径.
⌒
⌒
⌒
解:连接OC. 设弯路的半径为Rm,则OF=(R-90)m. ∵OE⊥CD
∴CF=-CD=-×600=300 (m)
由勾股定理,得 OC2= CF2 +OF2
R2 =3002 +(R-90 )2 解这个方程,得 R=545. 所以,这段弯路的半径为545m.
1
2
1
2
耐心填一填:
如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________.
·
M
O
A
B
N
C
2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 10
3. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.
AC=BC
A
C
⌒
⌒
AN=BN
⌒
⌒
AM=BM
⌒
⌒
0<x≤6
2或8
·
M
N
O
A
B
图2
图1
C
反思:在⊙ O中,若⊙ O的半径r、
圆心到弦的距离d、弦长a中,
任意知道两个量,可根据 定理求出第三个量:
1:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。
D
C
E
O
A
B
垂径
试一试:
解:连接OA,设⊙O的半径为Rcm,则 OA=Rcm, OD=R-CD=(R-2)cm, ∵CE为⊙O的直径, 且CD⊥AB ∴AD=AB/2=8/2=4cm 在Rt△AOD中, AO2 =AD2 +OD2 即 R2 =42 +(R-2)2 解这个方程,得 R=3 即半径OC的长为3cm.
C
D
B
A
O
r
d
a
探索:如图,AB是圆O的直径,CD为弦,AE⊥CD于点E, BF⊥CD于点F, EC和DF相等吗 说明理由.
A
C
E
O
B
M
D
F
解: EC=DF
理由是: 过点O作OM⊥ EF于M,由垂径定理得 CM=DM
∵AE⊥EF, OM⊥EF, BF⊥EF
∴ AE∥OM∥BF
∵ AO=BO
∴ EM=FM
∴ EM-CM=FM-DM
即EC=DF
一变:如图,若直线EF平移到与直径AB相交于点P ( 点 P不与点A、B重合),在其它条件不变下,原结论是否改变 为什么
·
C
A
B
D
O
M
F
E
2.已知:如图,在⊙O中,AB、AC为互相垂直的两条相等的弦,OD⊥AB,OE⊥AC,D、E为垂足。求证:ADOE为正方形。
O
A
B
C
D
E
课后练习
1. 在半径为50mm的⊙O中,有长50mm的弦AB。计算:
(1) 点O与AB的距离;
(2)∠AOB的度数。
O
A
B
小结:
3.方法:(1)垂径定理和勾股定理有机结合计算弦长、半径、弦心距等问题的方法,构造直角三角形; (2)解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
A
B
O
1.“垂直于弦的直径”是圆的重要性
质之一,也是全章的基础之一,
在整章中占有举足轻重的地位是今
后研究圆与其他图形位置关系和数量关系的基础,这些知识在日常生活和生产中有广泛的应用,由于垂径及推论反映了圆的重要性质,是证明线段相等、角相等、垂直关系的重要依据,因此,它是整节书的重点.
2.本课知识点:(1)圆的轴对称性;(2)垂径定理及应用.
同课章节目录
