垂径定理(复习)[上学期]
文档属性
| 名称 | 垂径定理(复习)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-27 14:10:00 | ||
图片预览


文档简介
课件14张PPT。垂直于弦的直径
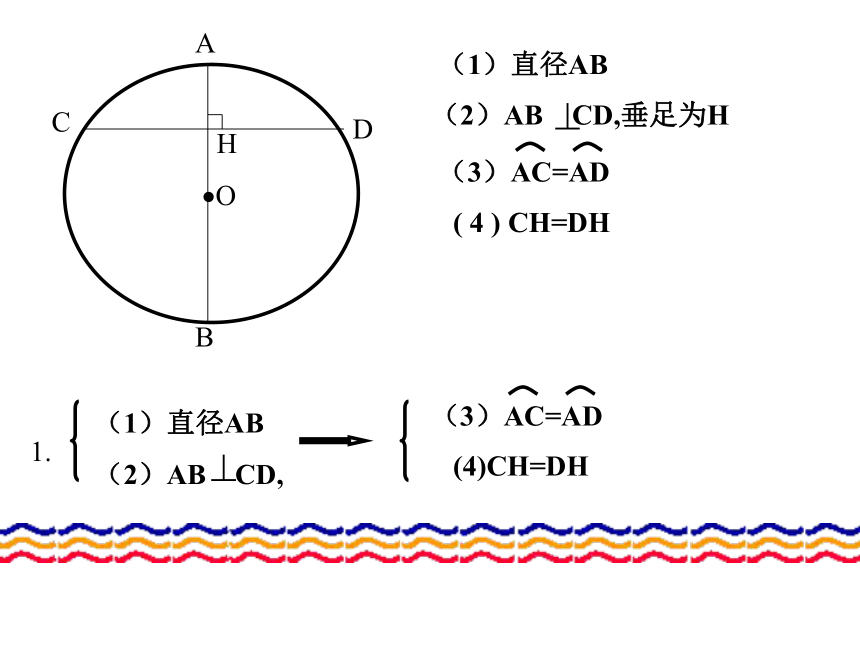
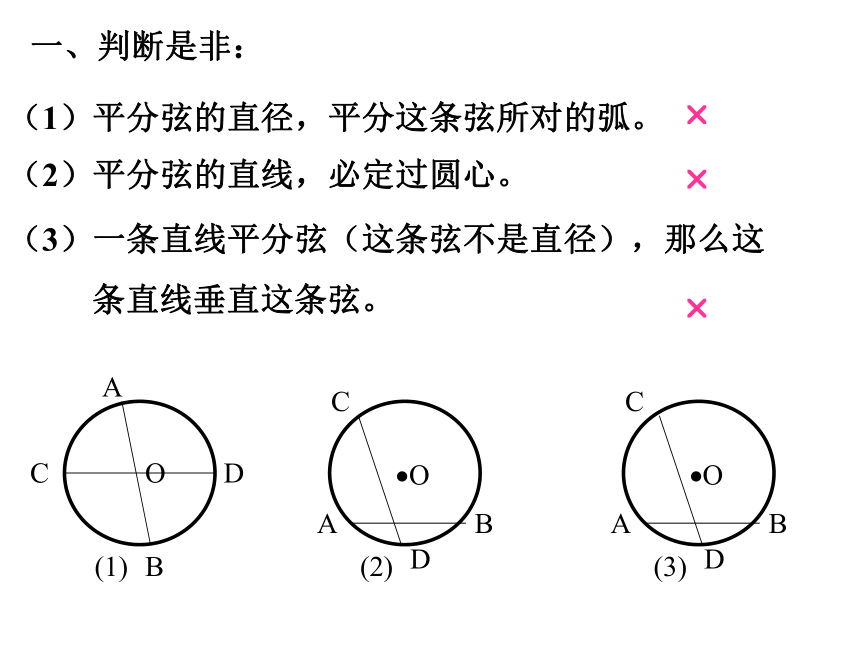
(复习)(1)直径AB( 4 ) CH=DH垂径定理的本质是二、练习三、小结四、达标检测一、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
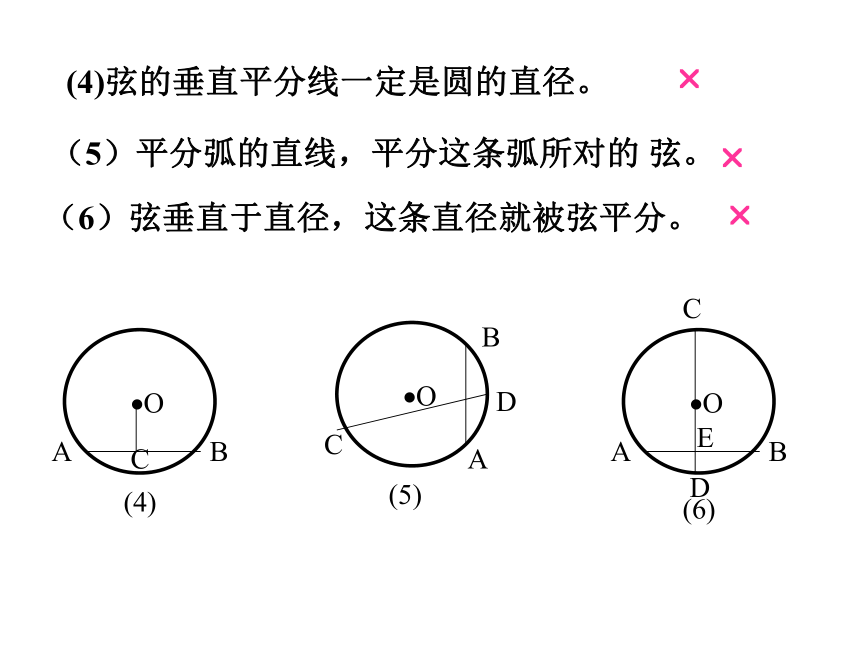
条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。??? 小结
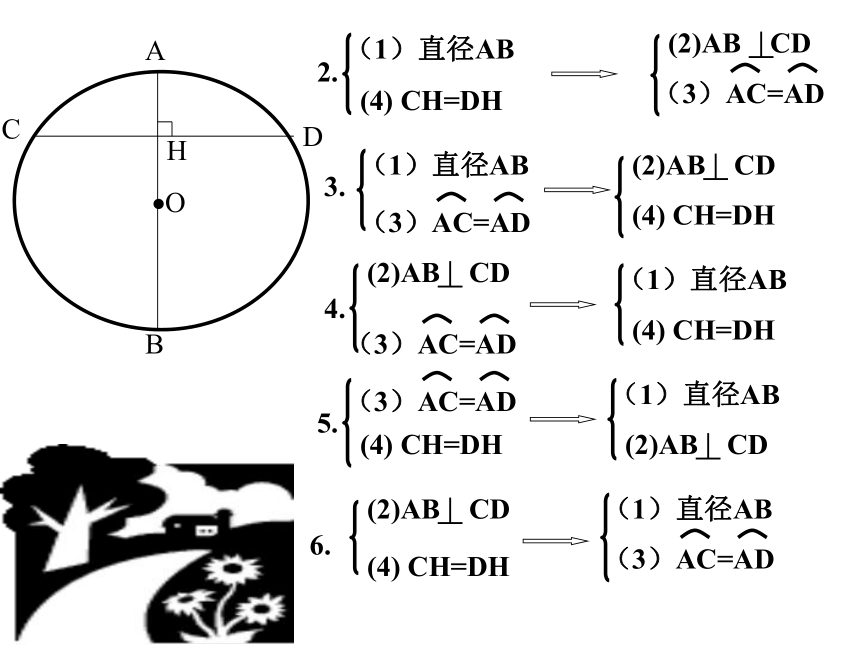
1.主要通过对圆中五种关系的两两组合,得出了除了垂径定理以外的圆的其它的性质。
2.注意这些性质必须同时满足两种关系才能运用。达标检测
一、填空
1、已知AB、CD是⊙O中互相垂直的弦,并且AB把CD分成3cm和7cm的两部分,则弦和圆心的距离为——cm.
2、已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为——.
3、已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为——
4、在半径为25cm的⊙O中,弦AB=40cm,则此弦和弦所对的弧的中点的距离是——
5、 ⊙O的直径AB=20cm, ∠BAC=30°则弦AC=——14cm或2cm25cm10cm和40cm
已知:如图,AB是的直径,CD是弦,AE⊥CD,垂足为E.
BF ⊥CD垂足为F.
求证:EC=DF已知:如图,AB是的直径,CD是弦,CE ⊥ CD,DF ⊥ CD
求证:AE=BFGGG一题多变变式提高OABC(1)已知⊙O的半径为4.5,它的内接ΔABC中,AB=AC,AD⊥BC于D,AD+AB=10,求AD的长。
(2)若D是BC的中点,AD ⊥BC,BC=24,
AD=9,求⊙O的半径。DBACDO(1)解:连结OB,延长AD,则必过圆心O。
若设AD=x,则OD=4.5-x,AB=10-x
在RtΔABD和RtΔOBD中,
BD2=AB2-AD2=OB2-OD2
即(10-x)2-x2 =4.52-(4.5-x)2
解得x=4 即AD=4如图,已知AB是⊙O的弦,MN是直径,MC⊥AB于C,
ND⊥AB于D.
1、求证:(1)AC=BD;(2)OC=OD2、若⊙O的半径为17cm,AB=30cm,求ND-MC
HEC 新颖题赏析
(复习)(1)直径AB( 4 ) CH=DH垂径定理的本质是二、练习三、小结四、达标检测一、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。??? 小结
1.主要通过对圆中五种关系的两两组合,得出了除了垂径定理以外的圆的其它的性质。
2.注意这些性质必须同时满足两种关系才能运用。达标检测
一、填空
1、已知AB、CD是⊙O中互相垂直的弦,并且AB把CD分成3cm和7cm的两部分,则弦和圆心的距离为——cm.
2、已知⊙O的半径为10cm,弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为——.
3、已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为——
4、在半径为25cm的⊙O中,弦AB=40cm,则此弦和弦所对的弧的中点的距离是——
5、 ⊙O的直径AB=20cm, ∠BAC=30°则弦AC=——14cm或2cm25cm10cm和40cm
已知:如图,AB是的直径,CD是弦,AE⊥CD,垂足为E.
BF ⊥CD垂足为F.
求证:EC=DF已知:如图,AB是的直径,CD是弦,CE ⊥ CD,DF ⊥ CD
求证:AE=BFGGG一题多变变式提高OABC(1)已知⊙O的半径为4.5,它的内接ΔABC中,AB=AC,AD⊥BC于D,AD+AB=10,求AD的长。
(2)若D是BC的中点,AD ⊥BC,BC=24,
AD=9,求⊙O的半径。DBACDO(1)解:连结OB,延长AD,则必过圆心O。
若设AD=x,则OD=4.5-x,AB=10-x
在RtΔABD和RtΔOBD中,
BD2=AB2-AD2=OB2-OD2
即(10-x)2-x2 =4.52-(4.5-x)2
解得x=4 即AD=4如图,已知AB是⊙O的弦,MN是直径,MC⊥AB于C,
ND⊥AB于D.
1、求证:(1)AC=BD;(2)OC=OD2、若⊙O的半径为17cm,AB=30cm,求ND-MC
HEC 新颖题赏析
同课章节目录
