22.1.2 二次函数y=ax2的图象和性质同步练习(含答案)
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象和性质同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 08:05:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
22.1.2二次函数y=ax 的图象和性质人教版数学 九年级上册
学校:______姓名:______班级:______考号:______
一、选择题
1. 抛物线,,的共同性质是:①都是开口向上;②都以点,为顶点;③都以轴为对称轴;④都关于轴对称.其中正确的个数为( )
A. B. C. D.
2.若二次函数的图象经过点,,则的值为( )
A. B. C. D.
3.抛物线一定经过( )
A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限
4.若二次函数的图象开口向上,则的值可能是( )
A. B. C. D.
5.下列二次函数的图象中,开口最大的是( )
A. B. C. D.
6.苹果熟了,从树上落下所经过的路程与下落时间满足,则与的函数图像大致是( )
A. B. C. D.
二、填空题
7.函数的图象开口向 ,对称轴是 ,顶点坐标是 .
8.已知二次函数的图象开口向下,则的取值范围是
9.抛物线的开口 ,当 时,有最 值,是 ;当 时,随的增大而减小.
10.当 时,抛物线的开口向上.此时,当时,随的增大而 ;当时,随的增大而 .
11.点,和,在函数的图象上,若,则与的大小关系为 ;若,则与的大小关系是 .
12.如图所示,①②③④.比较,,,的大小,用连接为 .
13.如图,正方形的边长为,以正方形中心为原点建立平面直角坐标系,作出函数与的图象,则阴影部分的面积是 .
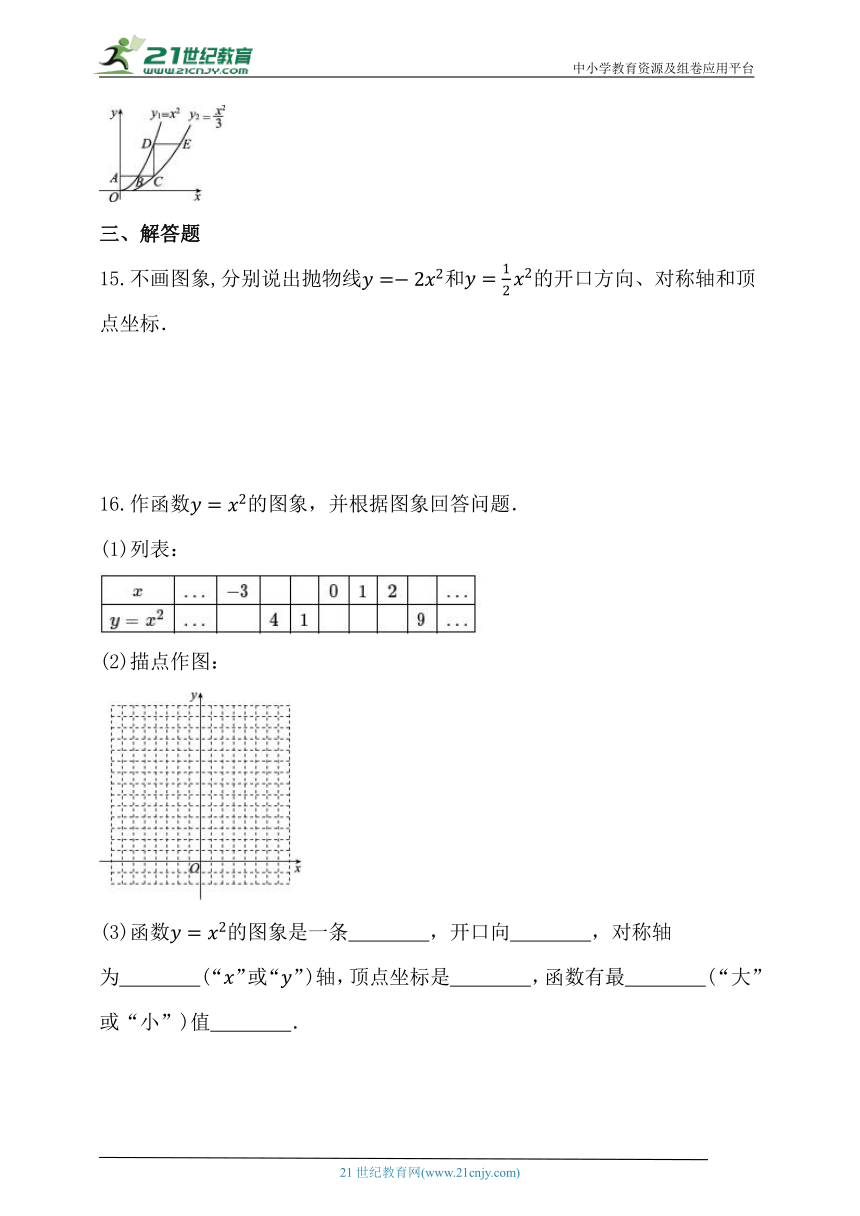
14.如图,平行于轴的直线分别交抛物线与于,两点,过点作轴的平行线交于点,直线,交于点,则 .
三、解答题
15.不画图象,分别说出抛物线和的开口方向、对称轴和顶点坐标.
16.作函数的图象,并根据图象回答问题.
(1)列表:
(2)描点作图:
(3)函数的图象是一条 ,开口向 ,对称轴为 (“”或“”)轴,顶点坐标是 ,函数有最 (“大”或“小”)值 .
参考答案
1.【答案】B
【解析】抛物线,的开口向上,的开口向下,①错误;
抛物线,,的顶点都为,,对称轴都为轴,②③正确;④错误.
故选
2.【答案】C
3.【答案】A
4.【答案】D
【解析】因为二次函数的图象开口向上,所以.
故选
5.【答案】C
【解析】【分析】由的绝对值越大其开口越小进行选择即可.
【解答】解:在( )中,当的绝对值越大时其开口越小,
∵| ,
∴二次函数 的开口最大,
故选.
6.【答案】B
7.【答案】上;轴;
8.【答案】
9.【答案】向下 ;;大;;
【解析】因为的二次项系数小于,所以抛物线的开口向下,有最大值
10.【答案】;减小;增大
11.【答案】;
12.【答案】
13.【答案】
【解析】函数与的图象关于轴对称,
图中的阴影部分的面积是图中正方形面积的一半,而边长为的正方形面积为,
图中的阴影部分的面积是.
14.【答案】
【解析】设点的坐标为,,令,解得负值已舍去),
∴点,.令,
则负值已舍去),
∴点,.∵轴,
∴点的横坐标与点的横坐标相同,为,
∴点的纵坐标为,
∴点的坐标为,.
∵,∴点的纵坐标为.
令,∴,
∴点的坐标为,,
∴.
故
15.【答案】抛物线的开口向下, 对称轴为轴,顶点坐标为. 抛物线的开口向上, 对称轴为轴,顶点坐标为
【解析】抛物线的开口向下, 对称轴为轴,顶点坐标为. 抛物线的开口向上, 对称轴为轴,顶点坐标为
16.【答案】(1)解:填表如下:
(2)如图所示.
(3)抛物线;上;;;小;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.1.2二次函数y=ax 的图象和性质人教版数学 九年级上册
学校:______姓名:______班级:______考号:______
一、选择题
1. 抛物线,,的共同性质是:①都是开口向上;②都以点,为顶点;③都以轴为对称轴;④都关于轴对称.其中正确的个数为( )
A. B. C. D.
2.若二次函数的图象经过点,,则的值为( )
A. B. C. D.
3.抛物线一定经过( )
A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限
4.若二次函数的图象开口向上,则的值可能是( )
A. B. C. D.
5.下列二次函数的图象中,开口最大的是( )
A. B. C. D.
6.苹果熟了,从树上落下所经过的路程与下落时间满足,则与的函数图像大致是( )
A. B. C. D.
二、填空题
7.函数的图象开口向 ,对称轴是 ,顶点坐标是 .
8.已知二次函数的图象开口向下,则的取值范围是
9.抛物线的开口 ,当 时,有最 值,是 ;当 时,随的增大而减小.
10.当 时,抛物线的开口向上.此时,当时,随的增大而 ;当时,随的增大而 .
11.点,和,在函数的图象上,若,则与的大小关系为 ;若,则与的大小关系是 .
12.如图所示,①②③④.比较,,,的大小,用连接为 .
13.如图,正方形的边长为,以正方形中心为原点建立平面直角坐标系,作出函数与的图象,则阴影部分的面积是 .
14.如图,平行于轴的直线分别交抛物线与于,两点,过点作轴的平行线交于点,直线,交于点,则 .
三、解答题
15.不画图象,分别说出抛物线和的开口方向、对称轴和顶点坐标.
16.作函数的图象,并根据图象回答问题.
(1)列表:
(2)描点作图:
(3)函数的图象是一条 ,开口向 ,对称轴为 (“”或“”)轴,顶点坐标是 ,函数有最 (“大”或“小”)值 .
参考答案
1.【答案】B
【解析】抛物线,的开口向上,的开口向下,①错误;
抛物线,,的顶点都为,,对称轴都为轴,②③正确;④错误.
故选
2.【答案】C
3.【答案】A
4.【答案】D
【解析】因为二次函数的图象开口向上,所以.
故选
5.【答案】C
【解析】【分析】由的绝对值越大其开口越小进行选择即可.
【解答】解:在( )中,当的绝对值越大时其开口越小,
∵| ,
∴二次函数 的开口最大,
故选.
6.【答案】B
7.【答案】上;轴;
8.【答案】
9.【答案】向下 ;;大;;
【解析】因为的二次项系数小于,所以抛物线的开口向下,有最大值
10.【答案】;减小;增大
11.【答案】;
12.【答案】
13.【答案】
【解析】函数与的图象关于轴对称,
图中的阴影部分的面积是图中正方形面积的一半,而边长为的正方形面积为,
图中的阴影部分的面积是.
14.【答案】
【解析】设点的坐标为,,令,解得负值已舍去),
∴点,.令,
则负值已舍去),
∴点,.∵轴,
∴点的横坐标与点的横坐标相同,为,
∴点的纵坐标为,
∴点的坐标为,.
∵,∴点的纵坐标为.
令,∴,
∴点的坐标为,,
∴.
故
15.【答案】抛物线的开口向下, 对称轴为轴,顶点坐标为. 抛物线的开口向上, 对称轴为轴,顶点坐标为
【解析】抛物线的开口向下, 对称轴为轴,顶点坐标为. 抛物线的开口向上, 对称轴为轴,顶点坐标为
16.【答案】(1)解:填表如下:
(2)如图所示.
(3)抛物线;上;;;小;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
