人教版高中数学必修第一册第二章2.2 基本不等式 课时3 基本不等式(1)(共30张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册第二章2.2 基本不等式 课时3 基本不等式(1)(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 10:01:44 | ||
图片预览











文档简介
(共30张PPT)
第二章
等式性质与不等式性质
2.2 基本不等式
课时3 基本不等式(1)
教学目标
1. 结合实例,从情境中抽象、归纳出算术平均数和几何平均数的概念,从特殊到一般猜想、发现基本不等式.
2. 通过对基本不等式几何意义的探究,感受数学文化之美,体会数形结合的魅力.
3. 探索基本不等式的证明过程,学会用作差法、综合法、分析法证明基本不等式.
学习目标
课程目标 学科核心素养
理解、掌握基本不等式的内容和结构 通过由完全平方公式到基本不等式的过程,培养逻辑推理素养
能够利用不等式的性质证明基本不等式,初步理解分析法的证明方法 借助基本不等式的证明过程,培养逻辑推理、数学运算素养
情境导学
在北京召开的第24届国际数学家大会的会标(如图1),是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民的热情好客.
图1 图2
如果将图中直角三角形的两条直角边的长度分别设为a,b(如图2所示),你能发现随着直角边长a,b的变化,这个弦图的大正方形和直角三角形的面积间有怎样的不等关系吗?用代替a,代替b后,这个不等式又有什么变化?
【活动1】 认识算术平均数与几何平均数
【问题1】从情境导学中,我们了解到,在日常生活中,我们经常会碰到用和表示的量,你知道它们的名称吗?
初探新知
【问题3】什么是基本不等式 你能证明基本不等式吗
【活动3】理解基本不等式的“内涵”和“外延”,掌
握基本不等式的证明方法
【问题4】如果将基本不等式的条件:正数a,b中的“正数”去掉,基本不等式还成立吗?为什么?
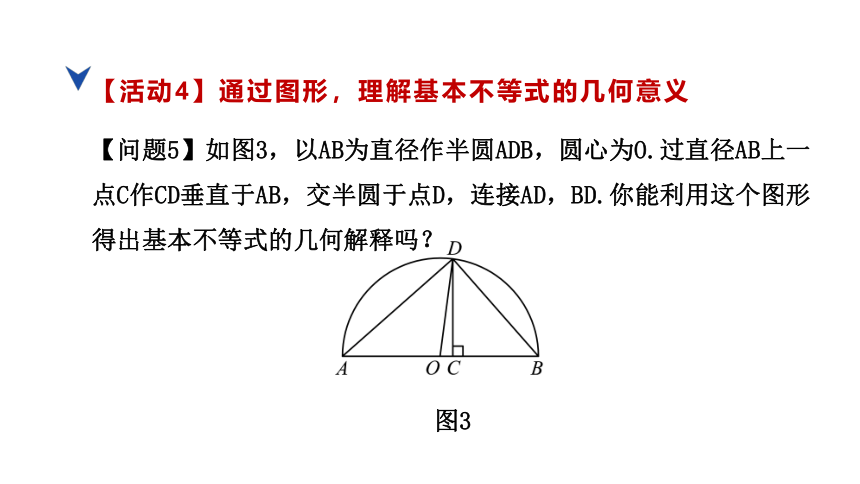
【问题5】如图3,以AB为直径作半圆ADB,圆心为O.过直径AB上一点C作CD垂直于AB,交半圆于点D,连接AD,BD.你能利用这个图形得出基本不等式的几何解释吗?
图3
【活动4】通过图形,理解基本不等式的几何意义
【问题6】基本不等式与不等式a2+b2≥2ab在结构上有什么联系和区别?
【活动5】认识基本不等式和不等式a2+b2≥2ab的关系
【问题7】基本不等式中的a,b均为正数,而a2+b2≥2ab中的a,b有无此要求?
典例精析
思路点拨:从基本不等式成立的条件入手,对每个选项进行判断.
【例1】
D
【解】
【方法规律】
在基本不等式应用过程中要注意“一正”“二定”“三相等”.一正,a,b均为正数;二定,不等式一边为定值;三相等,不等式中的等号能取到,即a=b有解.
【变式训练1】(多选) [教材改编题]下列选项中能使+≥2成立的有( )
A. ab>0 B. ab<0 C. a>0,b>0 D. a<0,b<0
【解】
当 均为正数时, ,故只需a,b同号即可,所
以ACD均满足要求.故选ACD
ACD
【例2】 [2022·天津市高三三模改编题]若0思路点拨:利用基本不等式及作差法比较大小,也可运用特殊值法进行求解.
【解】因为02,a2+b2>2ab,所以四个数中最大的应从a+b,a2+b2中选择.而a2+b2-(a+b)=a(a-1)+b(b-1),因为0【方法规律】
(1) 在使用基本不等式时,要注意不等式的双向性.
① 从左到右:常使用基本不等式的变形公式ab≤()2
(当且仅当a=b时取等号);
② 从右到左:常使用a+b≥2(a>0,b>0,当且仅当a=b时取等号).
(2) 运用基本不等式比较大小应注意等号成立的条件.
(3) 特殊值法是解决不等式的一个有效方法,但要使特殊值具有一般性.
【变式训练2】已知a,b是不相等的正数,x= ,y= ,试比较x,y的大小.
【解】
已知a,b是不相等的正数,由 ,
又因为
【例3】已知a,b为正实数,求证:(a+b)()≥4.
思路点拨 由a, b为正实数,可考虑运用基本不等式证明.
【解】
【方法规律】
对已知符合基本不等式条件的不等式进行证明,应首先考虑运用基本不等式直接证明.证明方法1是先展开,再运用基本不等式证明;证明方法2是直接运用基本不等式,得到两个同向正数不等式,再运用不等式的性质两边相乘得到要证的不等式。
【变式训练3】
已知ab>0,且a≠b,求证:ab+++>4.
【解】
(备选例题)
(1) 设a,b,c均为正实数,求证:a+b+c≥++;
(2) 设a,b,c为不全相等的正实数,且a+b+c=1,求证:>8.
思路点拨 (1) 由待证的不等式形式引发用基本不等求解的想法.
(2) 由于不等式右边的常数“8”,产生直觉——对左边运用三次基本不等式进行放缩.
【证明】
a,b,c均为正实数,可得a+b≥2,b+c≥2,c+a≥2,三式相加可得(a+b)+(b+c)+(c+a)≥2+2+2,即a+b+c≥++.
(2) 由a+b+c=1,可得-1==,同理可得-1=,-1=,故而=.由a,b,c均为正实数,可得b+c≥2>0,c+a≥2>0,a+b≥2>0,从而(b+c)(c+a)(a+b)≥2·2·2=8abc,当且仅当b=c且c=a且a=b,即a=b=c=时等号成立,但a,b,c不全相等,故等号不成立,因此(b+c)(c+a)(a+b)>8abc,即>8.
【方法规律】
(1) 证明不等式的方法比较灵活,常用的有:比较法、综合法和分析法等.对涉及正数的条件以及具有和、积的结构特征等的不等式证明,运用基本不等式直接证明常可取到简捷明快的效果.(2) 在证明不等式的过程中,要注意不等式的基本性质的正确应用.
课堂反思
通过本节课的学习,你学到了哪些知识?
2.你认为本节课的重点和难点是什么?
随堂演练
A
AD
D
4. 若a>1,则a+与3的大小关系是 .
a+≥3
同学们再见!
Goodbye Students!
第二章
等式性质与不等式性质
2.2 基本不等式
课时3 基本不等式(1)
教学目标
1. 结合实例,从情境中抽象、归纳出算术平均数和几何平均数的概念,从特殊到一般猜想、发现基本不等式.
2. 通过对基本不等式几何意义的探究,感受数学文化之美,体会数形结合的魅力.
3. 探索基本不等式的证明过程,学会用作差法、综合法、分析法证明基本不等式.
学习目标
课程目标 学科核心素养
理解、掌握基本不等式的内容和结构 通过由完全平方公式到基本不等式的过程,培养逻辑推理素养
能够利用不等式的性质证明基本不等式,初步理解分析法的证明方法 借助基本不等式的证明过程,培养逻辑推理、数学运算素养
情境导学
在北京召开的第24届国际数学家大会的会标(如图1),是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民的热情好客.
图1 图2
如果将图中直角三角形的两条直角边的长度分别设为a,b(如图2所示),你能发现随着直角边长a,b的变化,这个弦图的大正方形和直角三角形的面积间有怎样的不等关系吗?用代替a,代替b后,这个不等式又有什么变化?
【活动1】 认识算术平均数与几何平均数
【问题1】从情境导学中,我们了解到,在日常生活中,我们经常会碰到用和表示的量,你知道它们的名称吗?
初探新知
【问题3】什么是基本不等式 你能证明基本不等式吗
【活动3】理解基本不等式的“内涵”和“外延”,掌
握基本不等式的证明方法
【问题4】如果将基本不等式的条件:正数a,b中的“正数”去掉,基本不等式还成立吗?为什么?
【问题5】如图3,以AB为直径作半圆ADB,圆心为O.过直径AB上一点C作CD垂直于AB,交半圆于点D,连接AD,BD.你能利用这个图形得出基本不等式的几何解释吗?
图3
【活动4】通过图形,理解基本不等式的几何意义
【问题6】基本不等式与不等式a2+b2≥2ab在结构上有什么联系和区别?
【活动5】认识基本不等式和不等式a2+b2≥2ab的关系
【问题7】基本不等式中的a,b均为正数,而a2+b2≥2ab中的a,b有无此要求?
典例精析
思路点拨:从基本不等式成立的条件入手,对每个选项进行判断.
【例1】
D
【解】
【方法规律】
在基本不等式应用过程中要注意“一正”“二定”“三相等”.一正,a,b均为正数;二定,不等式一边为定值;三相等,不等式中的等号能取到,即a=b有解.
【变式训练1】(多选) [教材改编题]下列选项中能使+≥2成立的有( )
A. ab>0 B. ab<0 C. a>0,b>0 D. a<0,b<0
【解】
当 均为正数时, ,故只需a,b同号即可,所
以ACD均满足要求.故选ACD
ACD
【例2】 [2022·天津市高三三模改编题]若0
【解】因为0
(1) 在使用基本不等式时,要注意不等式的双向性.
① 从左到右:常使用基本不等式的变形公式ab≤()2
(当且仅当a=b时取等号);
② 从右到左:常使用a+b≥2(a>0,b>0,当且仅当a=b时取等号).
(2) 运用基本不等式比较大小应注意等号成立的条件.
(3) 特殊值法是解决不等式的一个有效方法,但要使特殊值具有一般性.
【变式训练2】已知a,b是不相等的正数,x= ,y= ,试比较x,y的大小.
【解】
已知a,b是不相等的正数,由 ,
又因为
【例3】已知a,b为正实数,求证:(a+b)()≥4.
思路点拨 由a, b为正实数,可考虑运用基本不等式证明.
【解】
【方法规律】
对已知符合基本不等式条件的不等式进行证明,应首先考虑运用基本不等式直接证明.证明方法1是先展开,再运用基本不等式证明;证明方法2是直接运用基本不等式,得到两个同向正数不等式,再运用不等式的性质两边相乘得到要证的不等式。
【变式训练3】
已知ab>0,且a≠b,求证:ab+++>4.
【解】
(备选例题)
(1) 设a,b,c均为正实数,求证:a+b+c≥++;
(2) 设a,b,c为不全相等的正实数,且a+b+c=1,求证:>8.
思路点拨 (1) 由待证的不等式形式引发用基本不等求解的想法.
(2) 由于不等式右边的常数“8”,产生直觉——对左边运用三次基本不等式进行放缩.
【证明】
a,b,c均为正实数,可得a+b≥2,b+c≥2,c+a≥2,三式相加可得(a+b)+(b+c)+(c+a)≥2+2+2,即a+b+c≥++.
(2) 由a+b+c=1,可得-1==,同理可得-1=,-1=,故而=.由a,b,c均为正实数,可得b+c≥2>0,c+a≥2>0,a+b≥2>0,从而(b+c)(c+a)(a+b)≥2·2·2=8abc,当且仅当b=c且c=a且a=b,即a=b=c=时等号成立,但a,b,c不全相等,故等号不成立,因此(b+c)(c+a)(a+b)>8abc,即>8.
【方法规律】
(1) 证明不等式的方法比较灵活,常用的有:比较法、综合法和分析法等.对涉及正数的条件以及具有和、积的结构特征等的不等式证明,运用基本不等式直接证明常可取到简捷明快的效果.(2) 在证明不等式的过程中,要注意不等式的基本性质的正确应用.
课堂反思
通过本节课的学习,你学到了哪些知识?
2.你认为本节课的重点和难点是什么?
随堂演练
A
AD
D
4. 若a>1,则a+与3的大小关系是 .
a+≥3
同学们再见!
Goodbye Students!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
