四川省达州市达川区达州2022-2023学年九年级下学期期中数学试题(无答案)
文档属性
| 名称 | 四川省达州市达川区达州2022-2023学年九年级下学期期中数学试题(无答案) | 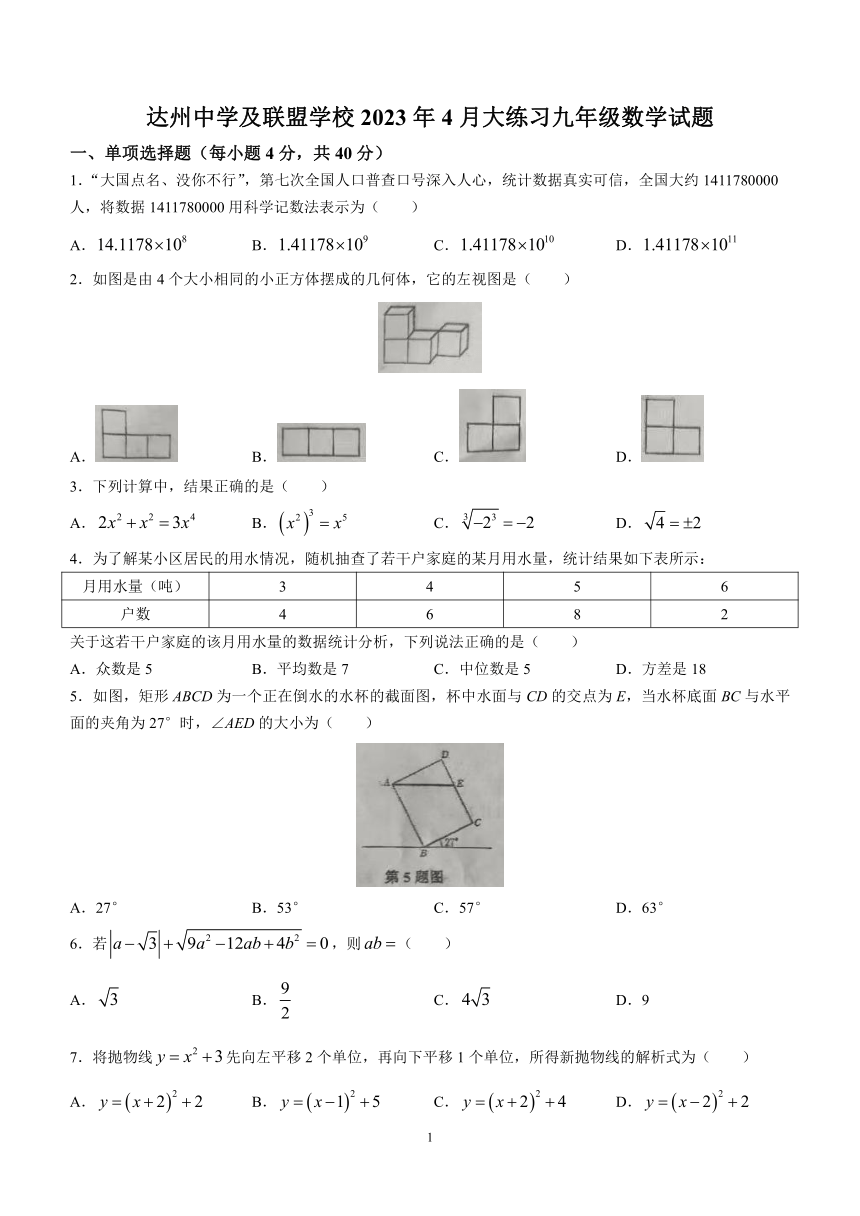 | |
| 格式 | doc | ||
| 文件大小 | 828.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 11:04:18 | ||
图片预览



文档简介
达州中学及联盟学校2023年4月大练习九年级数学试题
一、单项选择题(每小题4分,共40分)
1.“大国点名、没你不行”,第七次全国人口普查口号深入人心,统计数据真实可信,全国大约1411780000
人,将数据1411780000用科学记数法表示为( )
A. B. C. D.
2.如图是由4个大小相同的小正方体摆成的几何体,它的左视图是( )
A. B. C. D.
3.下列计算中,结果正确的是( )
A. B. C. D.
4.为了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如下表所示:
月用水量(吨) 3 4 5 6
户数 4 6 8 2
关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的是( )
A.众数是5 B.平均数是7 C.中位数是5 D.方差是18
5.如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
A.27° B.53° C.57° D.63°
6.若,则( )
A. B. C. D.9
7.将抛物线先向左平移2个单位,再向下平移1个单位,所得新抛物线的解析式为( )
A. B. C. D.
8.中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个 其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个,问:苦、甜果各有几个 设苦果有x个,甜果有y个,则可列方程组为( )
A. B. C. D.
9.如图,在正方形ABCD中,点P是AB上动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点B、F,交AD、BC于点M、N.下列结论:①;②;③;④;⑤点O在M、N两点的连线上,其中正确的结论序号是( )
A.①②③④ B.①②③⑤ C.①②③④⑤ D.③④⑤
10.如图所示,已知二次函数的图象与x轴交于,两点,与y轴的正半轴交于点C,顶点为D,则下列结论:①;②;③当是等胆三角形时,a的值有2个;④当是直角三角形时,,其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共20分)
11.已知,,则______.
12.如图,和是以点O为位似中心的位似图形.若,则与的周长比是______.
13.点,在反比例函数的图象上,若,则a的范围是______.
14.如图,线段,分别以点A,点B为圆心,以6为半径作弧,两弧交于点C,点D,连接CD.则CD的长为______.
15.规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若M、N的坐标分别为,,P是二次函数的图象上在第一象限内的任意一点,PQ垂直直线于点Q,则四边形PMNQ是广义菱形,其中正确的是______.(填序号)
三、解答题(本大题共10小题,共90分)
16.(本题共两小题,每小题4分,共8分)
(1)计算:.
(2)先化简,再求值:,其中.
17.(本题满分8分)“只要人人都献出点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂相款”活动倡议,有2500名居民踊跃参与献爱心,社区管理员随机抽查了部分居民捐款情况,统计图如图:
(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
18.(本题满分8分)在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°,已知山坡坡度,即,请你帮助该小组计算建筑物的高度AB.(结果精确到0.1m,参考数据:)
19.(本题满分8分)如图,网格中小正方形的边长为1,
(1)画出关于x轴对称的(其中、、分别为A、B、C的对应点);
(2)的面积为______;点B到边AC的距离为______;
(3)在x轴上是否存在一点M,使得最小,若存在,请直接写出的最小值;若不存在,请说明原因.
20.(本题满分8分)如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,,连接EF.
(1)求证:;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O.若,,求AO的长.
21.(本题满分9分)端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价x元(),表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.
22.(本题满分9分)如图,AB是的一条弦,E是AB的中点,过点E作于点C,这点B作的切线交CE的延长线于点D.
(1)求证:;
(2)若,,求的半径.
23.(本题满分10分)已知一次函数(a为常数)与x轴交于点A,与反比例函数交于B、C两点,B点的横坐标为-2.
(1)求出一次函数的解析式并在图中画出它的图象;
(2)求出点C的坐标,并根据图象写出当时对应自变量x的取值范围;
(3)若点B与点D关于原点成中心对称,求出的面积.
24.(本题满分10分)已知抛物线经过点、.
(1)求抛物线的解析式;
(2)若点A在直线PQ上,过点A作轴于点B,以AB为斜边在其左侧作等腰直角三角形ABC.
①当Q与A重合时,求C到抛物线对称轴的距离;
②若C在抛物线上,求C的坐标.
25.(12分)如图1,在矩形ABCD中,AB=1,对角线AC,BD相交于点O,,点E是线段CD上一点,连接OE,将线段OE绕点O逆时针旋转60°得到线段OF,连接DF.
(1)求证:;
(2)连接EF交OD于点P,求DP的最大值;
(3)如图2,点E在射线CD上运动,连接AF,在点E的运动过程中,若,求OF的长.
一、单项选择题(每小题4分,共40分)
1.“大国点名、没你不行”,第七次全国人口普查口号深入人心,统计数据真实可信,全国大约1411780000
人,将数据1411780000用科学记数法表示为( )
A. B. C. D.
2.如图是由4个大小相同的小正方体摆成的几何体,它的左视图是( )
A. B. C. D.
3.下列计算中,结果正确的是( )
A. B. C. D.
4.为了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如下表所示:
月用水量(吨) 3 4 5 6
户数 4 6 8 2
关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的是( )
A.众数是5 B.平均数是7 C.中位数是5 D.方差是18
5.如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
A.27° B.53° C.57° D.63°
6.若,则( )
A. B. C. D.9
7.将抛物线先向左平移2个单位,再向下平移1个单位,所得新抛物线的解析式为( )
A. B. C. D.
8.中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个 其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个,问:苦、甜果各有几个 设苦果有x个,甜果有y个,则可列方程组为( )
A. B. C. D.
9.如图,在正方形ABCD中,点P是AB上动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点B、F,交AD、BC于点M、N.下列结论:①;②;③;④;⑤点O在M、N两点的连线上,其中正确的结论序号是( )
A.①②③④ B.①②③⑤ C.①②③④⑤ D.③④⑤
10.如图所示,已知二次函数的图象与x轴交于,两点,与y轴的正半轴交于点C,顶点为D,则下列结论:①;②;③当是等胆三角形时,a的值有2个;④当是直角三角形时,,其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共20分)
11.已知,,则______.
12.如图,和是以点O为位似中心的位似图形.若,则与的周长比是______.
13.点,在反比例函数的图象上,若,则a的范围是______.
14.如图,线段,分别以点A,点B为圆心,以6为半径作弧,两弧交于点C,点D,连接CD.则CD的长为______.
15.规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若M、N的坐标分别为,,P是二次函数的图象上在第一象限内的任意一点,PQ垂直直线于点Q,则四边形PMNQ是广义菱形,其中正确的是______.(填序号)
三、解答题(本大题共10小题,共90分)
16.(本题共两小题,每小题4分,共8分)
(1)计算:.
(2)先化简,再求值:,其中.
17.(本题满分8分)“只要人人都献出点爱,世界将变成美好的人间”,在新型肺炎疫情期间,全国人民万众一心,众志成城,共克时艰.某社区积极发起“援鄂相款”活动倡议,有2500名居民踊跃参与献爱心,社区管理员随机抽查了部分居民捐款情况,统计图如图:
(1)计算本次共抽查居民人数,并将条形图补充完整;
(2)根据统计情况,请估计该社区捐款20元以上(含20元)的居民有多少人
(3)该社区有1名男管理员和3名女管理员,现要从中随机挑选2名管理员参与“社区防控”宣讲活动,请用列表法或树状图法求出恰好选到“1男1女”的概率.
18.(本题满分8分)在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°,已知山坡坡度,即,请你帮助该小组计算建筑物的高度AB.(结果精确到0.1m,参考数据:)
19.(本题满分8分)如图,网格中小正方形的边长为1,
(1)画出关于x轴对称的(其中、、分别为A、B、C的对应点);
(2)的面积为______;点B到边AC的距离为______;
(3)在x轴上是否存在一点M,使得最小,若存在,请直接写出的最小值;若不存在,请说明原因.
20.(本题满分8分)如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,,连接EF.
(1)求证:;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O.若,,求AO的长.
21.(本题满分9分)端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉粽和用6000元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价x元(),表示该商家每天销售猪肉粽的利润(单位:元),求y关于x的函数解析式并求最大利润.
22.(本题满分9分)如图,AB是的一条弦,E是AB的中点,过点E作于点C,这点B作的切线交CE的延长线于点D.
(1)求证:;
(2)若,,求的半径.
23.(本题满分10分)已知一次函数(a为常数)与x轴交于点A,与反比例函数交于B、C两点,B点的横坐标为-2.
(1)求出一次函数的解析式并在图中画出它的图象;
(2)求出点C的坐标,并根据图象写出当时对应自变量x的取值范围;
(3)若点B与点D关于原点成中心对称,求出的面积.
24.(本题满分10分)已知抛物线经过点、.
(1)求抛物线的解析式;
(2)若点A在直线PQ上,过点A作轴于点B,以AB为斜边在其左侧作等腰直角三角形ABC.
①当Q与A重合时,求C到抛物线对称轴的距离;
②若C在抛物线上,求C的坐标.
25.(12分)如图1,在矩形ABCD中,AB=1,对角线AC,BD相交于点O,,点E是线段CD上一点,连接OE,将线段OE绕点O逆时针旋转60°得到线段OF,连接DF.
(1)求证:;
(2)连接EF交OD于点P,求DP的最大值;
(3)如图2,点E在射线CD上运动,连接AF,在点E的运动过程中,若,求OF的长.
同课章节目录
