用例举法求概率(1)[上学期]
文档属性
| 名称 | 用例举法求概率(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 291.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-28 20:43:27 | ||
图片预览








文档简介
课件22张PPT。用例举法求概率(1)事件A的概率: 一般地,在大量重复进行同一试验时,事件A发生的频率 总稳定在某个常数p的附近,这个常数叫做事件A的概率,记作P(A)= p 。温故知新②当频率在某个常数附近摆动时,这个常数叫做
事件A的概率③概率是频率的稳定值,而频率是概率的近似值。④概率反映了随机事件发生的可能性的大小。⑤必然事件的概率是1,不可能事件的概率是0,
因此事件A的概率为0≤P(A)≤1说明:①求一个事件概率的基本方法是通过大量的重
复的实验。
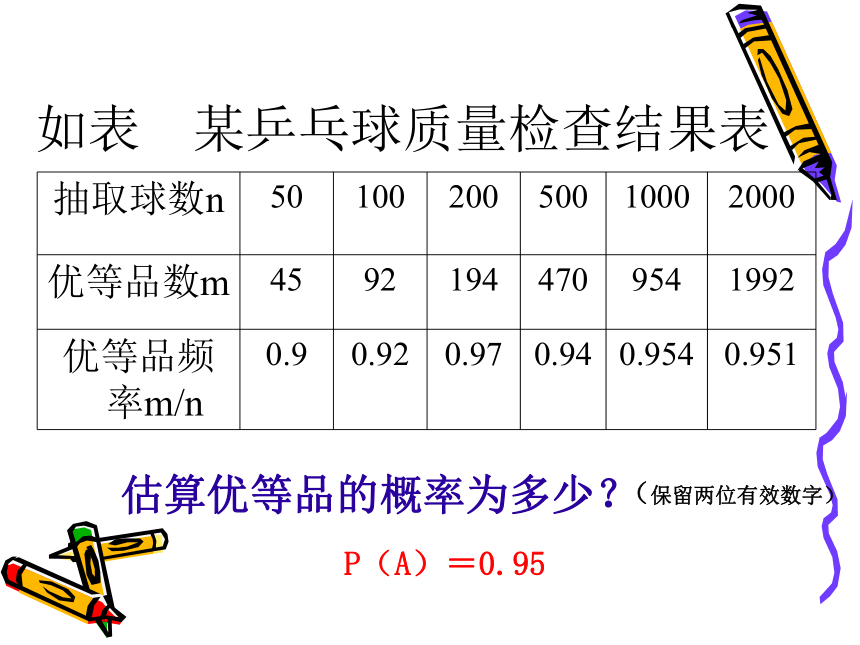
但随机事件的概率的范围呢?如表 某乒乓球质量检查结果表估算优等品的概率为多少?(保留两位有效数字)P(A)=0.95自主学习1、什么是等可能事件?
2、如何求一件等可能事件的概率?等可能性事件问题1.掷一枚硬币,朝上的面有 种可能。
问题2.抛掷一个骰子,它落地时向上的的数 有 种可能。
问题3.从标有1,2,3,4,5号的纸签中随意地抽取一根,抽出的签上的号码有 种可能。265以上三个试验有两个共同的特点:1。 一次试验中,可能出现的结果有限多个。
2。一次试验中,各种结果发生的可能性相等。问题1.掷一枚硬币,朝上的面有 种可能。
问题2.抛掷一个骰子,它落地时向上的的数 有 种可能。
问题3.从标有1,2,3,4,5号的纸签中随意地抽取一根,抽出的签上的号码有 种可能。265P(反面朝上)= P(点数为2)=P(点数为奇数)=P(点数大于2且小于5)=P(抽到偶数号)=P(小于7的号)=归纳:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=思考?在P(A)= 中 ,分子m 和分母n都表示结果的数目,它们之间有怎样的数量关系?n≥m例1:下列事件哪些是等可能性事件?哪些不是?抛掷一枚图钉,钉尖朝上或钉帽朝上或横卧。
某运动员射击一次中靶心或不中靶心。
从分别写有1,3,5,7中的一个数的四张卡片中任抽一张结果是1,或3或5或7。
2.等可能性事件的概率问题1.掷一枚一硬币,正面向上的概率是多少?
问题2.抛掷一个骰子,它落地时向上的的数为1的概率是多少?
问题3.抛掷一个骰子,落地时向上的数是3的倍数的概率是多少?例2 如图是一个转盘,转盘分成7个相同的扇形,颜色分为红、绿、黄 三种。指针位置固定,转动转盘后任其自由停止,指针会停在某个扇形里。求下列事件的概率:(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。当堂反馈 1袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则P(摸到红球)= ;P(摸到白球)= ;P(摸到黄 球)= 。抢答题:2、彩票有100张,分别标有1,2,3,…100的号码,只有摸中的号码是7的倍数的彩券才有奖,小明随机地摸出一张,那么他中奖的概率是多少?
3、一张圆桌旁有4个座位,A先坐在如图所示的位置上,B、C、D随机地坐到其它三个座位上,求A与B不相邻而坐的概率。4、 一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球.
(1)共有多少种不同的结果?
(2)摸出2个黑球有多种不同的结果?
(3)摸出两个黑球的概率是多少?5、将骰子先后抛掷2次,计算:
(1)一共有多少种不同的结果?
(2)其中向上的数之和是5的结果有多少种?
(3)向上的数这和是5的概率是多少?6、在100件产品中,有95件合格品,5件次品。从中任取2件,计算:
(1)2件都是合格品的概率;
(2)2件都是次品的概率;
(3)1件是合格品、1件是次品的概率.1、某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券(转盘被等分20个扇形).(4)他得到20元购物券的概率是多少?(1)甲顾客的消费额120元,他获得购物券的概率是多少?(2)他得到100元购物券的概率是多少?(3)他得到50元购物券的概率是多少?应用与体会 1. 如图所示,转盘被等分为16个扇形。请在转盘的适当地方涂上颜色,使得自由转动这个转盘,当它停止转动时①指针落在红色区域的概率为 。②你还能再举出一个不确定事件,使得它发生的概率也是 吗?设计与提高 2.如图:请你为班会活动设计一个可以自由转动的8等分转盘,要求所设计的方案满足下列两个条件: (1)指针停在红色区域和停在黄色区域的概率相同; (2)指针停在蓝色区域的概率大于停在红色区域的概率.
如果除了满足(1)(2)两个条件外,再增加条件:(3)指针停在蓝色区域的概率大于为0.5
你设计的方案是什么?小结:课后日记:
今天学了什么:___________ 今天的收获是:______________ 不明白的地方是:____________再见
事件A的概率③概率是频率的稳定值,而频率是概率的近似值。④概率反映了随机事件发生的可能性的大小。⑤必然事件的概率是1,不可能事件的概率是0,
因此事件A的概率为0≤P(A)≤1说明:①求一个事件概率的基本方法是通过大量的重
复的实验。
但随机事件的概率的范围呢?如表 某乒乓球质量检查结果表估算优等品的概率为多少?(保留两位有效数字)P(A)=0.95自主学习1、什么是等可能事件?
2、如何求一件等可能事件的概率?等可能性事件问题1.掷一枚硬币,朝上的面有 种可能。
问题2.抛掷一个骰子,它落地时向上的的数 有 种可能。
问题3.从标有1,2,3,4,5号的纸签中随意地抽取一根,抽出的签上的号码有 种可能。265以上三个试验有两个共同的特点:1。 一次试验中,可能出现的结果有限多个。
2。一次试验中,各种结果发生的可能性相等。问题1.掷一枚硬币,朝上的面有 种可能。
问题2.抛掷一个骰子,它落地时向上的的数 有 种可能。
问题3.从标有1,2,3,4,5号的纸签中随意地抽取一根,抽出的签上的号码有 种可能。265P(反面朝上)= P(点数为2)=P(点数为奇数)=P(点数大于2且小于5)=P(抽到偶数号)=P(小于7的号)=归纳:一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为P(A)=思考?在P(A)= 中 ,分子m 和分母n都表示结果的数目,它们之间有怎样的数量关系?n≥m例1:下列事件哪些是等可能性事件?哪些不是?抛掷一枚图钉,钉尖朝上或钉帽朝上或横卧。
某运动员射击一次中靶心或不中靶心。
从分别写有1,3,5,7中的一个数的四张卡片中任抽一张结果是1,或3或5或7。
2.等可能性事件的概率问题1.掷一枚一硬币,正面向上的概率是多少?
问题2.抛掷一个骰子,它落地时向上的的数为1的概率是多少?
问题3.抛掷一个骰子,落地时向上的数是3的倍数的概率是多少?例2 如图是一个转盘,转盘分成7个相同的扇形,颜色分为红、绿、黄 三种。指针位置固定,转动转盘后任其自由停止,指针会停在某个扇形里。求下列事件的概率:(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。当堂反馈 1袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则P(摸到红球)= ;P(摸到白球)= ;P(摸到黄 球)= 。抢答题:2、彩票有100张,分别标有1,2,3,…100的号码,只有摸中的号码是7的倍数的彩券才有奖,小明随机地摸出一张,那么他中奖的概率是多少?
3、一张圆桌旁有4个座位,A先坐在如图所示的位置上,B、C、D随机地坐到其它三个座位上,求A与B不相邻而坐的概率。4、 一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球.
(1)共有多少种不同的结果?
(2)摸出2个黑球有多种不同的结果?
(3)摸出两个黑球的概率是多少?5、将骰子先后抛掷2次,计算:
(1)一共有多少种不同的结果?
(2)其中向上的数之和是5的结果有多少种?
(3)向上的数这和是5的概率是多少?6、在100件产品中,有95件合格品,5件次品。从中任取2件,计算:
(1)2件都是合格品的概率;
(2)2件都是次品的概率;
(3)1件是合格品、1件是次品的概率.1、某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:顾客每购买100元的商品就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券(转盘被等分20个扇形).(4)他得到20元购物券的概率是多少?(1)甲顾客的消费额120元,他获得购物券的概率是多少?(2)他得到100元购物券的概率是多少?(3)他得到50元购物券的概率是多少?应用与体会 1. 如图所示,转盘被等分为16个扇形。请在转盘的适当地方涂上颜色,使得自由转动这个转盘,当它停止转动时①指针落在红色区域的概率为 。②你还能再举出一个不确定事件,使得它发生的概率也是 吗?设计与提高 2.如图:请你为班会活动设计一个可以自由转动的8等分转盘,要求所设计的方案满足下列两个条件: (1)指针停在红色区域和停在黄色区域的概率相同; (2)指针停在蓝色区域的概率大于停在红色区域的概率.
如果除了满足(1)(2)两个条件外,再增加条件:(3)指针停在蓝色区域的概率大于为0.5
你设计的方案是什么?小结:课后日记:
今天学了什么:___________ 今天的收获是:______________ 不明白的地方是:____________再见
同课章节目录
