概率的意义[上学期]

课件18张PPT。25.1.2 概率的意义在一定条件下必然发生的事件，叫做
在一定条件下不可能发生的事件，叫做
在一定条件下可能发生也可能不发生的事件，叫做
温故知新必然事件不可能事件随机事件 一种彩票的中奖率1%，某人买了100张彩票，那么他中奖是一个 件。
想 一 想随机 在同样条件下，随机事件可能发生，也可能不发生，那么它发生的可能性有多大呢？这是我们下面要讨论的问题。我们从抛掷硬币这个简单问题说起。探究：硬币抛掷试验试验要求：
（1）每4个人一组，分成10组，每一组抛掷50次。
（2）记录“正面向上”的次数
（3）在抛掷过程中采取同一种方法都往上扔，拿手把它接住，这样可以保证在同一条件下。
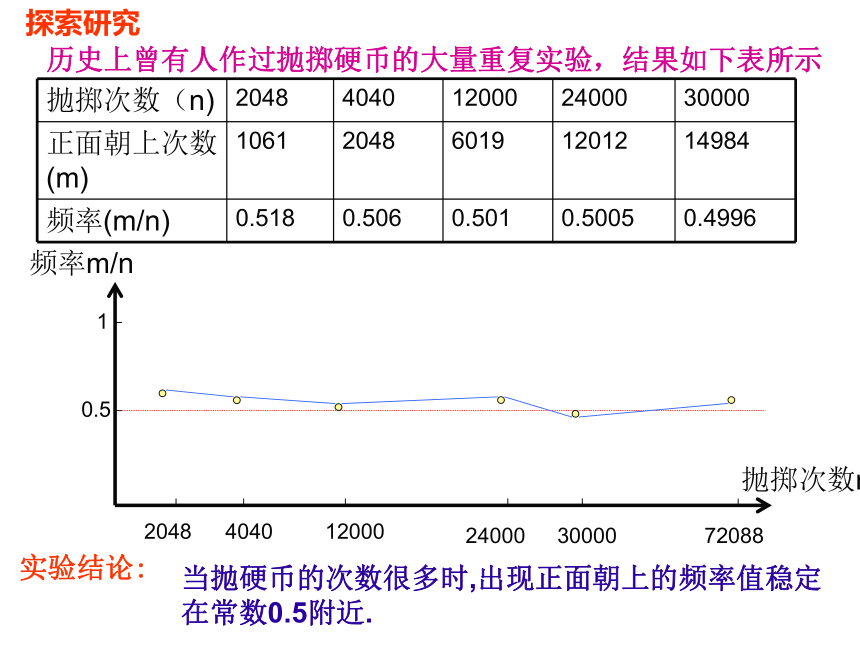
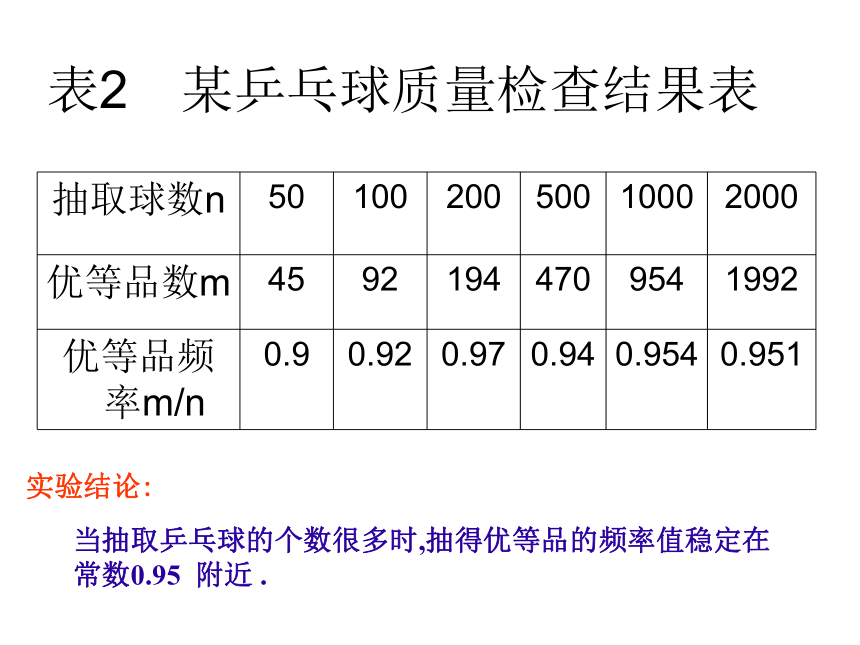
（4）本着严肃认真、严谨求实这样一种科学精神，通过实验学会相互合作、相互沟通。试验结果历史上曾有人作过抛掷硬币的大量重复实验，结果如下表所示探索研究实验结论:当抛硬币的次数很多时,出现正面朝上的频率值稳定在常数0.5附近.表2　某乒乓球质量检查结果表实验结论:当抽取乒乓球的个数很多时,抽得优等品的频率值稳定在常数0.95 附近 .表3　某种油菜籽在相同条件下的发芽试验结果表实验结论:当油菜籽的粒数很多时,能发芽的频率值稳定在常数0.9 附近 .概率（Probability)的定义：一般地，在大量重复进行同一试验时，事件A发生的频率m/n稳定在某个常数p的附近，那么这个常数就叫做思考？必然事件的概率和不可能事件的概率分别是多少呢？.P(必然事件)＝1P(不可能事件)＝0事件A的概率，记作P（A）=p.记随机事件A在n次试验中发生了m次，那么有0≤m≤n,
0≤m/n≤1
于是可得　　0≤P(A) ≤1.
显然，必然事件的概率是1，不可能事件的概率是0.试 练 平 台 下表记录了一名球员在罚球线上投篮的结果。（1）计算表中投中频率（精确到0.01）；
（2）这名球员投篮一次，投中的概率约是多少 （精确到0.1）？
0.560.500.520.600.520.490.510.5当堂反馈某射手在同一条件下进行射击，结果如下表所示：(1)计算表中击中靶心的各个频率；(精确到0,01)
（2）这个射击一次，击中靶心的概率约是多少？(精确到0,1)
0.800.950.880.920.890.910.900.51说明下列事件的概率，并标在图上请你来帮忙(1)(2)(3)(4) 掷一粒骰子,正面朝上的数字是 3 的倍数.(4) 1、 任意掷一枚均匀的硬币，前9次都是正面朝上，当他掷第10次时，你认为正面朝上的概率是 。0.5平心静气，展示智慧 2.大家试验，抛掷一个骰子，它落地时向上的数为1的概率是多少？1/6 3、小华用电脑设计了一个小猫跳转的实验，如图所示，图形由黑白两种颜色的20块方砖组成，方砖的大小完全一样，小猫在方砖上可自由走动并随意停止。
（1）在这个实验中，小猫停留在黑砖上的概率是多少？
（2）要使小猫停留在黑砖上的概率是0.6,在不改变方砖数目的情况下,其他颜色应作怎样的调整？平心静气，展示智慧8÷20=0.4黑砖需 20×0.6=12 块试 一试 飞的更高 天气预报说下星期一降水概率是90%，下星期三降水概率是10%，于是有位同学说：下星期一肯定下雨，下星期三肯定不下雨。你认为他说的对吗？ 不对。所谓降水概率90%、10%是在大量的统计记录的条件下，那么它是符合大多数同等天气条件下的实际情况的，但某些例外也还是可能的。想一想，你会更棒! 概率并不提供确定无误的结论，这是由随机现象的本质所决定的。那么，学习概率有用吗？智慧小结你如何理解概率的意义？