人教版数学七年级上册1.2.4绝对值 说课课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.2.4绝对值 说课课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 455.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 11:56:35 | ||
图片预览








文档简介
(共22张PPT)
绝对值
教法学法指导
4
教材分析
1
学情分析
3
教学目标分析
2
教学设计
5
板书设计
6
说课提纲
教材的地位和作用
内容:
思想:
绝对值概念突出显示了基本概念的重要性,是整个教学体系中的一个重要概念,体现了分类、方程、整体、数形结合等数学思想。
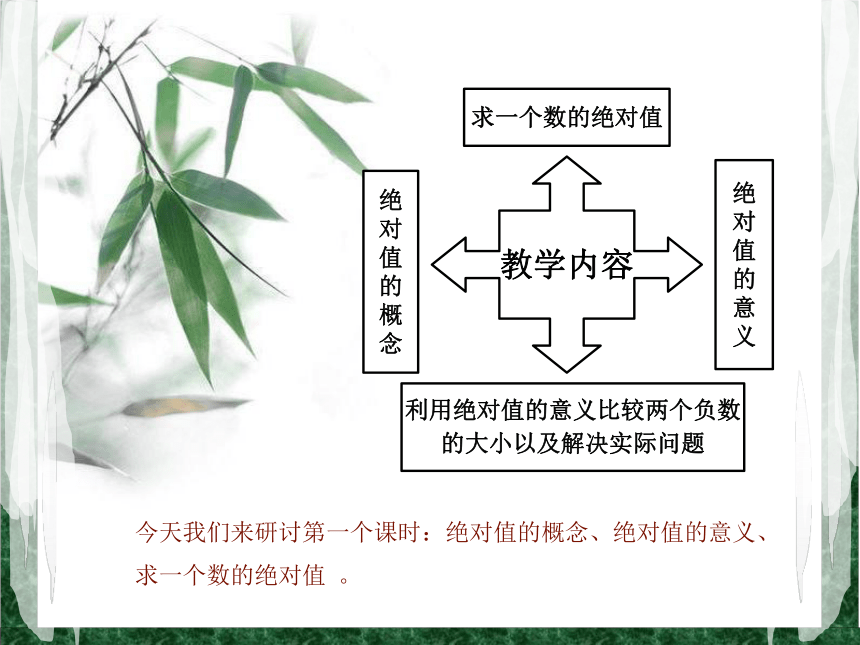
教学内容
求一个数的绝对值
利用绝对值的意义比较两个负数
的大小以及解决实际问题
今天我们来研讨第一个课时:绝对值的概念、绝对值的意义、求一个数的绝对值 。
绝
对
值
的
概
念
绝
对
值
的
意
义
教学目标分析
1、绝对值的意义
2、求一个数的绝对值
正确理解绝对值的意义,
当 a 是负数时,︱a︱=-a
教学重点、难点分析
重 点
难 点
学情分析
1、知识储备
学生已初步掌握了数轴和相反数的概念,能够用数轴上的点表示有理数。
2、智力和能力发展的年龄特征
七年级学生的思维正处于以具体形象思维成分为主向以抽象逻辑思维成分为主的转折期,但已经具备了一定的抽象能力和归纳能力,初步具备数形结合的思想。
3、心理特征
七年级学生具有思想活跃,求知欲旺盛,对事物有强烈的好奇心,注意力容易发散等特点。
教法学法指导
教学设计流程
一、情境引入(3min)
二、探究新知(20min)
三、例题讲解(6min)
四、巩固提高(12min)
五、课堂小结(3min)
六、布置作业(1min)
一、情景导入
1.它们的行驶路线相同吗
-10
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B 两处.
2.它们行驶的路程(线段OA、OB的长度)相等吗
O
B
A
10
设计意图:在生活中,有些问题我们只考虑数的大小而不考虑符号(即方向)。从“路程”抽象出“距离”,为引出绝对值的概念做铺垫。
二、探索新知
例如:在数轴上+3点,距离原点3个单位长度,即 +3的绝对值等于3,记作 │+3│=3。在数轴上-3点,距离原点3个单位长度,即 -3的绝对值等于3,记作 │-3│=3。
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|. (a可以取正数、负数和0)
绝对值:
0
1
2
3
4
-1
-2
-3
强调:|0|=0
二、探索新知
问题1:互为相反数的两个数的绝对值有什么关系?
问题2:绝对值相等的两个数有什么关系?
结论1:互为相反数的两个数的绝对值相等.
结论2:绝对值相等的两个数可能相等,也可能是互为相反数.
设计意图:借助数轴和举例,引导学生发现相反数与绝对值之间的关系。
设计意图:进一步巩固强化绝对值的概念,同时,通过求具体数的绝对值,为概括有理数的绝对值的代数意义做铺垫.
二、探索新知
想一想:一个数的绝对值与这个数有什么关系?
其绝对值可能是负数吗?为什么?
绝对值的代数意义:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
任何数的绝对值都是非负的,即|a|≥0
如果a>0,则|a|=a
如果a<0,则|a|=-a
如果a=0,则|a|=0
三、例题讲解
例1:求下列数的绝对值
; -3; -8;100
解:
=
;|-3|=3;|-8|=8;|100|=100
在利用绝对值的意义来求一个数的绝对值的时候,
关键是判断这个数的正负性。
三、例题讲解
例2、已知一个数的绝对值为 1.5,求这个数
分析:如图,因为数轴上到原点的距离等于1.5的 点有M、N两点,所以绝对值为1.5的数是1.5或-1.5
0
1.5
-1.5
即: |-1.5|=1.5 |1.5|=1.5
绝对值等于一个正数的数有两个,它们互为相反数。
四、巩固练习
3、判断下列各式是否正确:
(1)|5|=|-5|; (2)-|5|=|-5|; (3)-5=|-5|
1.字母a表示一个数,-a表示什么?-a一定是负数吗?
五、课堂小结
本节课学到了哪些知识?
有什么收获?
设计意图:让学生参与小结,自我评价学习效果,可增强学生学习的积极性和主动性,培养学生良好的学习习惯。通过小结也强化了本节的重点,有利于突破教学难点。
六、布置作业
A组:
1、数轴上表示2和5两点之间的距离是( ),表示-2和-5两点之间的距离是( ),表示1和-3两点之间的距离是( )。
2、-|-3|=( ),|-0.27|=( ),-|26|=( )
3. 如果|a| = 4,那么 a 等于________.
设计意图:强调绝对值等于一个数的数有两个,它们互为相反数
设计意图:加强绝对值概念和意义的练习,突破重点
六、布置作业
B组:
1、若|m-1|=m-1,则m_______1 ,
若|m-1|>m-1,则m_______1.
2、如果|a|=4, |b|=3,且a设计意图:遵循因材施教的原则,分层作业。A组为基础题,要求全部学生通过,B组为拔高题;其目的是对不同层次的学生提出不同要求,满足学生的需求,使中下学生“吃得了”,优生“吃得饱”。
3、如果|a+2|+|b-5|=0,则 a=_____,b=______.
绝对值
绝对值的概念:
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
绝对值的意义:
|a|=
a (a>0)
0 (a=0)
-a (a<0)
互为相反数的两个数的绝对值相等。
性质:|a|≥0
板书设计
例一:
例二:
Thank you!
绝对值
教法学法指导
4
教材分析
1
学情分析
3
教学目标分析
2
教学设计
5
板书设计
6
说课提纲
教材的地位和作用
内容:
思想:
绝对值概念突出显示了基本概念的重要性,是整个教学体系中的一个重要概念,体现了分类、方程、整体、数形结合等数学思想。
教学内容
求一个数的绝对值
利用绝对值的意义比较两个负数
的大小以及解决实际问题
今天我们来研讨第一个课时:绝对值的概念、绝对值的意义、求一个数的绝对值 。
绝
对
值
的
概
念
绝
对
值
的
意
义
教学目标分析
1、绝对值的意义
2、求一个数的绝对值
正确理解绝对值的意义,
当 a 是负数时,︱a︱=-a
教学重点、难点分析
重 点
难 点
学情分析
1、知识储备
学生已初步掌握了数轴和相反数的概念,能够用数轴上的点表示有理数。
2、智力和能力发展的年龄特征
七年级学生的思维正处于以具体形象思维成分为主向以抽象逻辑思维成分为主的转折期,但已经具备了一定的抽象能力和归纳能力,初步具备数形结合的思想。
3、心理特征
七年级学生具有思想活跃,求知欲旺盛,对事物有强烈的好奇心,注意力容易发散等特点。
教法学法指导
教学设计流程
一、情境引入(3min)
二、探究新知(20min)
三、例题讲解(6min)
四、巩固提高(12min)
五、课堂小结(3min)
六、布置作业(1min)
一、情景导入
1.它们的行驶路线相同吗
-10
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B 两处.
2.它们行驶的路程(线段OA、OB的长度)相等吗
O
B
A
10
设计意图:在生活中,有些问题我们只考虑数的大小而不考虑符号(即方向)。从“路程”抽象出“距离”,为引出绝对值的概念做铺垫。
二、探索新知
例如:在数轴上+3点,距离原点3个单位长度,即 +3的绝对值等于3,记作 │+3│=3。在数轴上-3点,距离原点3个单位长度,即 -3的绝对值等于3,记作 │-3│=3。
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|. (a可以取正数、负数和0)
绝对值:
0
1
2
3
4
-1
-2
-3
强调:|0|=0
二、探索新知
问题1:互为相反数的两个数的绝对值有什么关系?
问题2:绝对值相等的两个数有什么关系?
结论1:互为相反数的两个数的绝对值相等.
结论2:绝对值相等的两个数可能相等,也可能是互为相反数.
设计意图:借助数轴和举例,引导学生发现相反数与绝对值之间的关系。
设计意图:进一步巩固强化绝对值的概念,同时,通过求具体数的绝对值,为概括有理数的绝对值的代数意义做铺垫.
二、探索新知
想一想:一个数的绝对值与这个数有什么关系?
其绝对值可能是负数吗?为什么?
绝对值的代数意义:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
任何数的绝对值都是非负的,即|a|≥0
如果a>0,则|a|=a
如果a<0,则|a|=-a
如果a=0,则|a|=0
三、例题讲解
例1:求下列数的绝对值
; -3; -8;100
解:
=
;|-3|=3;|-8|=8;|100|=100
在利用绝对值的意义来求一个数的绝对值的时候,
关键是判断这个数的正负性。
三、例题讲解
例2、已知一个数的绝对值为 1.5,求这个数
分析:如图,因为数轴上到原点的距离等于1.5的 点有M、N两点,所以绝对值为1.5的数是1.5或-1.5
0
1.5
-1.5
即: |-1.5|=1.5 |1.5|=1.5
绝对值等于一个正数的数有两个,它们互为相反数。
四、巩固练习
3、判断下列各式是否正确:
(1)|5|=|-5|; (2)-|5|=|-5|; (3)-5=|-5|
1.字母a表示一个数,-a表示什么?-a一定是负数吗?
五、课堂小结
本节课学到了哪些知识?
有什么收获?
设计意图:让学生参与小结,自我评价学习效果,可增强学生学习的积极性和主动性,培养学生良好的学习习惯。通过小结也强化了本节的重点,有利于突破教学难点。
六、布置作业
A组:
1、数轴上表示2和5两点之间的距离是( ),表示-2和-5两点之间的距离是( ),表示1和-3两点之间的距离是( )。
2、-|-3|=( ),|-0.27|=( ),-|26|=( )
3. 如果|a| = 4,那么 a 等于________.
设计意图:强调绝对值等于一个数的数有两个,它们互为相反数
设计意图:加强绝对值概念和意义的练习,突破重点
六、布置作业
B组:
1、若|m-1|=m-1,则m_______1 ,
若|m-1|>m-1,则m_______1.
2、如果|a|=4, |b|=3,且a
3、如果|a+2|+|b-5|=0,则 a=_____,b=______.
绝对值
绝对值的概念:
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|。
绝对值的意义:
|a|=
a (a>0)
0 (a=0)
-a (a<0)
互为相反数的两个数的绝对值相等。
性质:|a|≥0
板书设计
例一:
例二:
Thank you!
