垂径定理1[上学期]
图片预览
文档简介
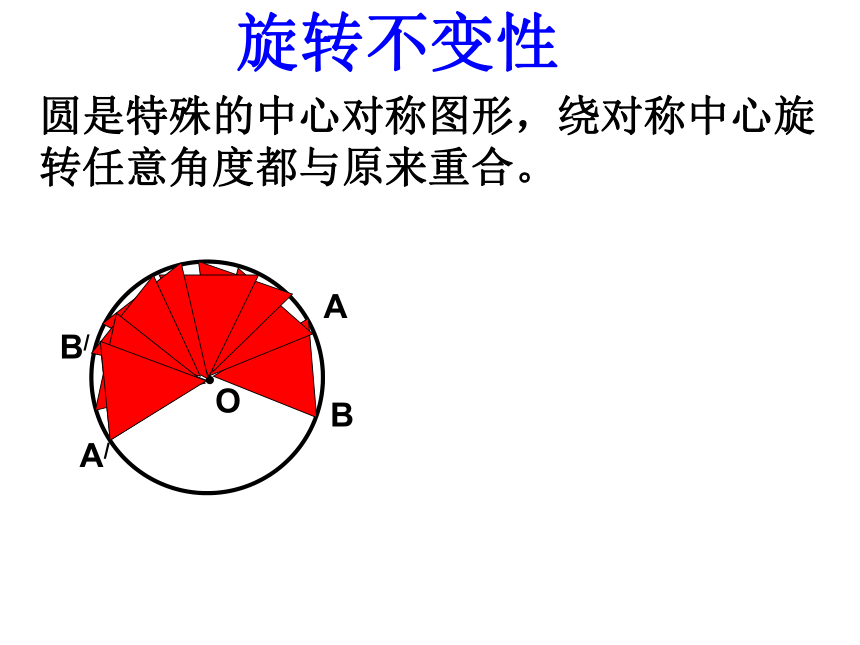
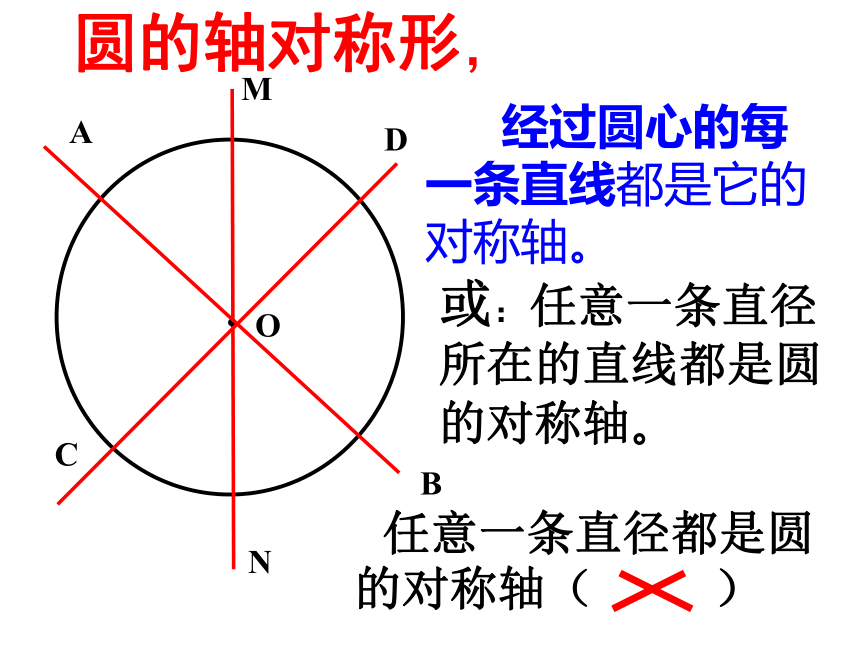
课件24张PPT。垂直于弦的直径(一)ABCDO圆既是中心对称图形,又是轴对称图形提问:圆是什么对称图形?圆是特殊的中心对称图形,绕对称中心旋转任意角度都与原来重合。旋转不变性BAA/OB/OACBNMD圆的轴对称形, 经过圆心的每一条直线都是它的对称轴。或:任意一条直径所在的直线都是圆的对称轴。 任意一条直径都是圆的对称轴( )如图:
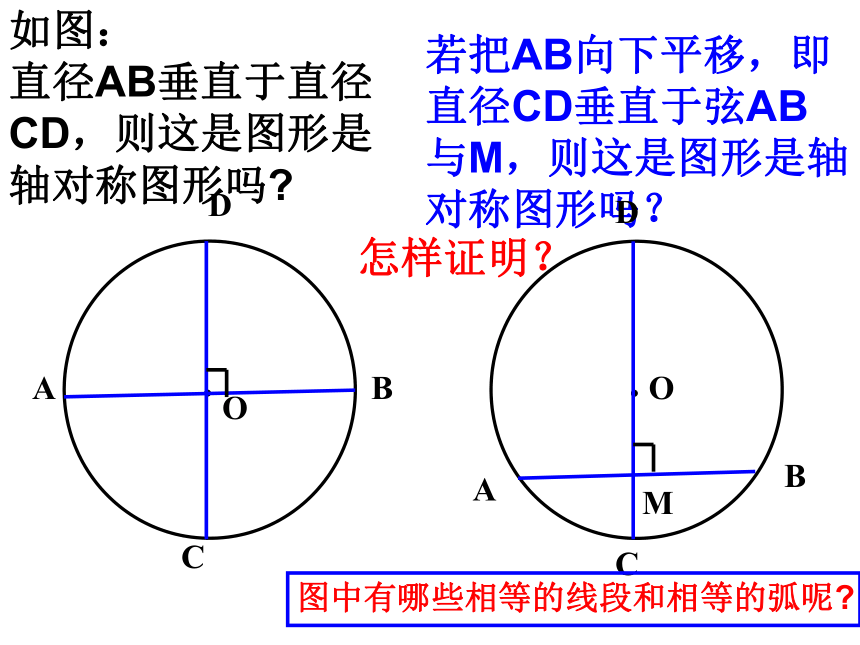
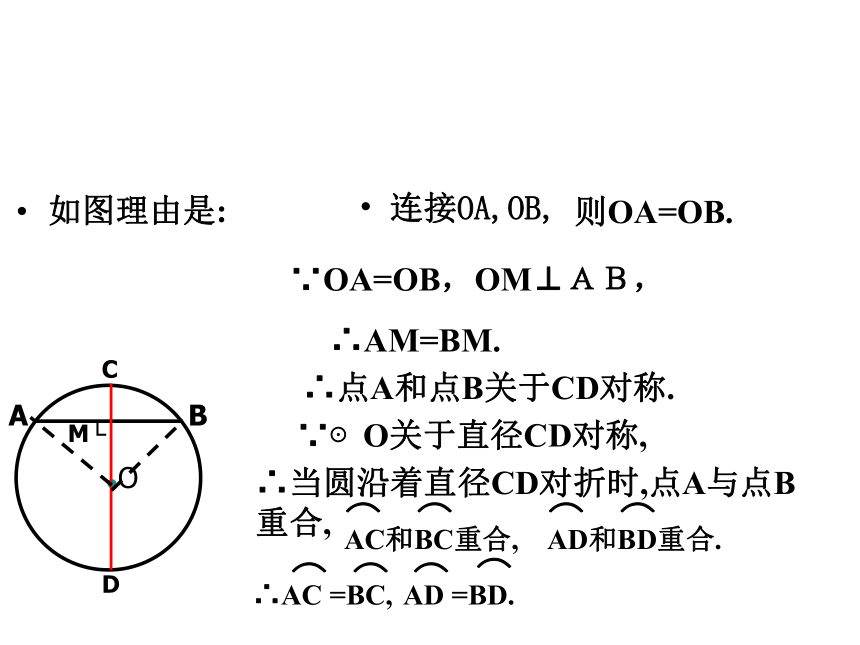
直径AB垂直于直径CD,则这是图形是轴对称图形吗?若把AB向下平移,即直径CD垂直于弦AB与M,则这是图形是轴对称图形吗?怎样证明? 图中有哪些相等的线段和相等的弧呢?如图理由是:连接OA,OB,则OA=OB.∵OA=OB,OM⊥AB,∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,AD 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:直径CD⊥弦AB与M,
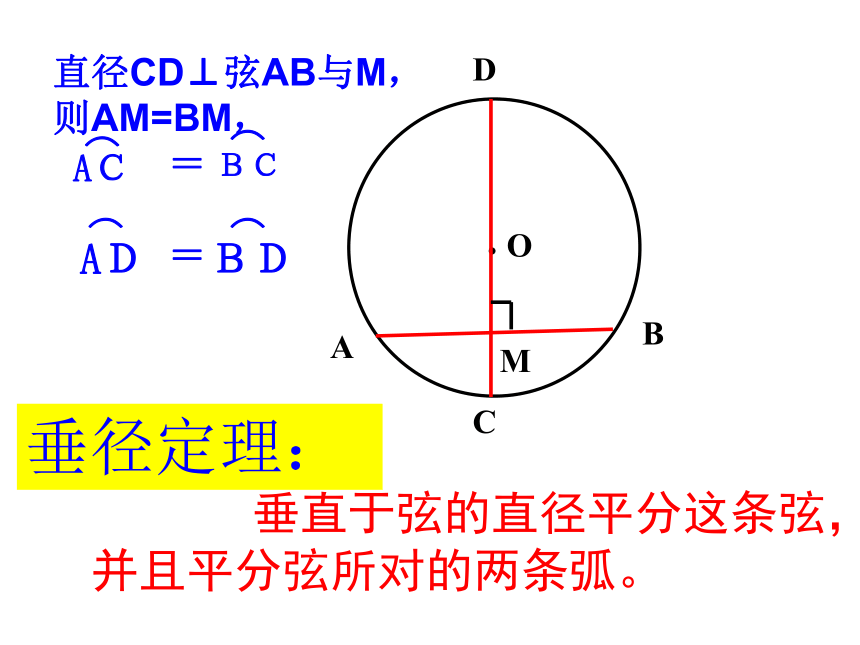
则AM=BM,
=
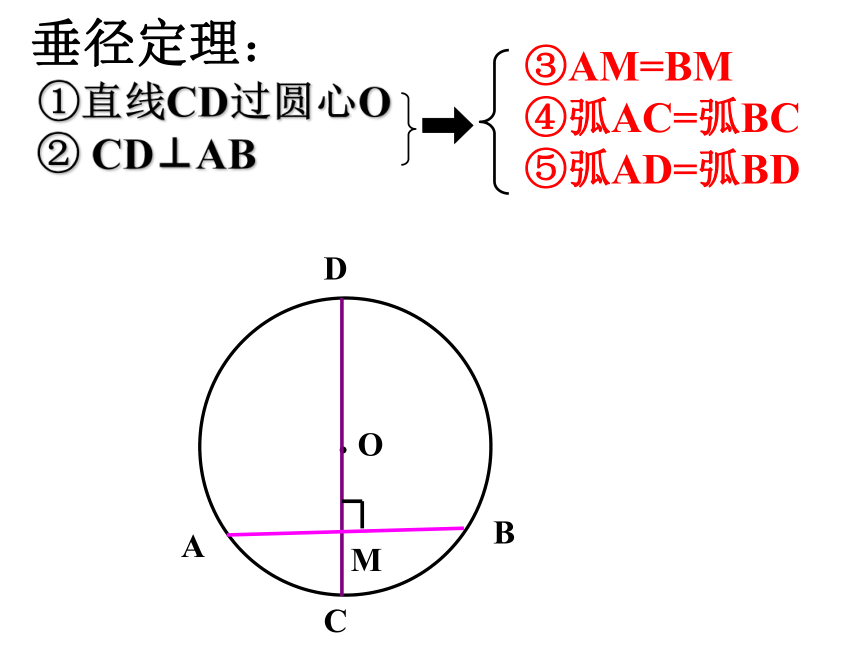
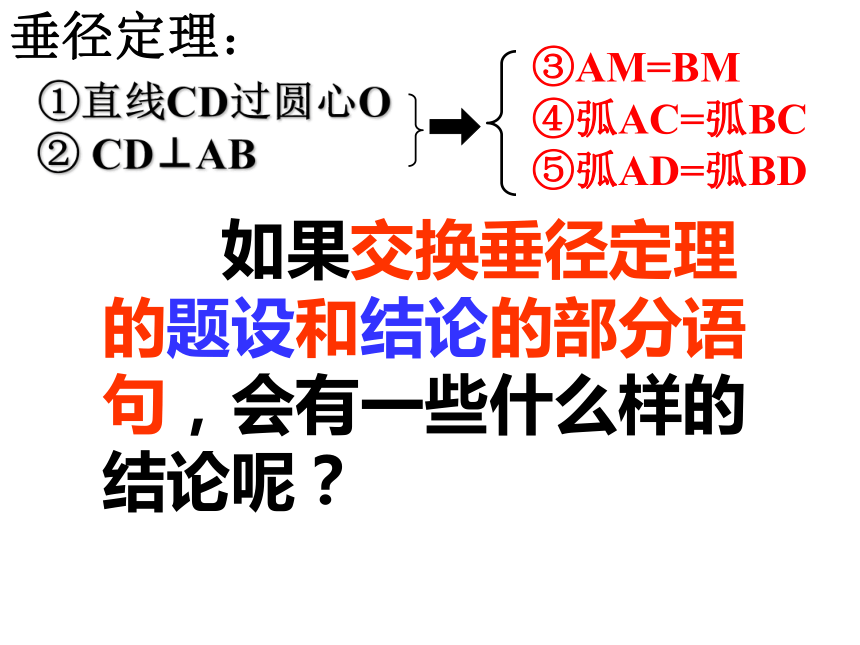
=⌒BC⌒BD⌒①直线CD过圆心O ② CD⊥AB③AM=BM
④弧AC=弧BC
⑤弧AD=弧BD垂径定理: 如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线CD过圆心O ② CD⊥AB③AM=BM
④弧AC=弧BC
⑤弧AD=弧BD垂径定理:①直线CD过圆心③ AM=BM
②CD⊥AB
④弧AC=弧BC ⑤弧AD=弧BD探索一:结论:推论1.(1)平分弦(不是直径)
的直径垂直于弦,
并且平分弦所对的两条弧。OABMN一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。CD辩一辩直径垂直弦,才能平分弦,平分弦所对的弧.例1.如图,弦AB的长为 8 cm,圆心O到 AB 的距离为 3 cm,求⊙O的半径.O ABE变式1.在⊙O中,直径为 10 cm,弦 AB的长为 8 cm, 求圆心O到AB的距离.变式2.在⊙O中,直径为 10 cm,圆心O到AB的距离为 3 cm,求弦AB的长.圆的半径为R,弦长为 a,弦心距为d,则 R 、a、d满足关系式
_________(? a)2+d2=R2应用1:垂径定理有关的计算题.练习:AB是⊙O的直径,弦CD⊥AB,E为垂足,若AE=9,BE=1,求CD的长.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________. 35 例2.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。 CD20152525247CDFFAB、CD在点O两侧EF=OE+OF=15+7=22AB、CD在点O同侧EF=OE-OF=15-7=8过点O作直线OE⊥AB,交CD于F。例3. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
试说明:AC=BD。E.ACDBO证明:过O作OE⊥AB于E∵OE⊥AB∴AE=EB∵OE⊥CD∴CE=ED∴AE-CE=EB-ED即AC=BD应用2:垂径定理有关的证明题.小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。练习: 在⊙O中,AB.CD为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.
求证:四边形ADOE是正方形.ABCODE已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF课堂小结请同学们谈谈你的收获-------再见
直径AB垂直于直径CD,则这是图形是轴对称图形吗?若把AB向下平移,即直径CD垂直于弦AB与M,则这是图形是轴对称图形吗?怎样证明? 图中有哪些相等的线段和相等的弧呢?如图理由是:连接OA,OB,则OA=OB.∵OA=OB,OM⊥AB,∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,AD 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理:直径CD⊥弦AB与M,
则AM=BM,
=
=⌒BC⌒BD⌒①直线CD过圆心O ② CD⊥AB③AM=BM
④弧AC=弧BC
⑤弧AD=弧BD垂径定理: 如果交换垂径定理的题设和结论的部分语句,会有一些什么样的结论呢?①直线CD过圆心O ② CD⊥AB③AM=BM
④弧AC=弧BC
⑤弧AD=弧BD垂径定理:①直线CD过圆心③ AM=BM
②CD⊥AB
④弧AC=弧BC ⑤弧AD=弧BD探索一:结论:推论1.(1)平分弦(不是直径)
的直径垂直于弦,
并且平分弦所对的两条弧。OABMN一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。CD辩一辩直径垂直弦,才能平分弦,平分弦所对的弧.例1.如图,弦AB的长为 8 cm,圆心O到 AB 的距离为 3 cm,求⊙O的半径.O ABE变式1.在⊙O中,直径为 10 cm,弦 AB的长为 8 cm, 求圆心O到AB的距离.变式2.在⊙O中,直径为 10 cm,圆心O到AB的距离为 3 cm,求弦AB的长.圆的半径为R,弦长为 a,弦心距为d,则 R 、a、d满足关系式
_________(? a)2+d2=R2应用1:垂径定理有关的计算题.练习:AB是⊙O的直径,弦CD⊥AB,E为垂足,若AE=9,BE=1,求CD的长.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____.最大值为____________. 35 例2.已知⊙O的直径是50 cm,⊙O的两条平行弦AB=40 cm ,CD=48cm,
求弦AB与CD之间的距离。 CD20152525247CDFFAB、CD在点O两侧EF=OE+OF=15+7=22AB、CD在点O同侧EF=OE-OF=15-7=8过点O作直线OE⊥AB,交CD于F。例3. 已知如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
试说明:AC=BD。E.ACDBO证明:过O作OE⊥AB于E∵OE⊥AB∴AE=EB∵OE⊥CD∴CE=ED∴AE-CE=EB-ED即AC=BD应用2:垂径定理有关的证明题.小结: 解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。练习: 在⊙O中,AB.CD为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E.
求证:四边形ADOE是正方形.ABCODE已知:AB是⊙O直径,CD
是弦,AE⊥CD,BF⊥CD
求证:EC=DF课堂小结请同学们谈谈你的收获-------再见
同课章节目录
