人教版数学七年级上册1.2.4绝对值 说课课件(共21张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.2.4绝对值 说课课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 614.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 12:01:41 | ||
图片预览




文档简介
(共21张PPT)
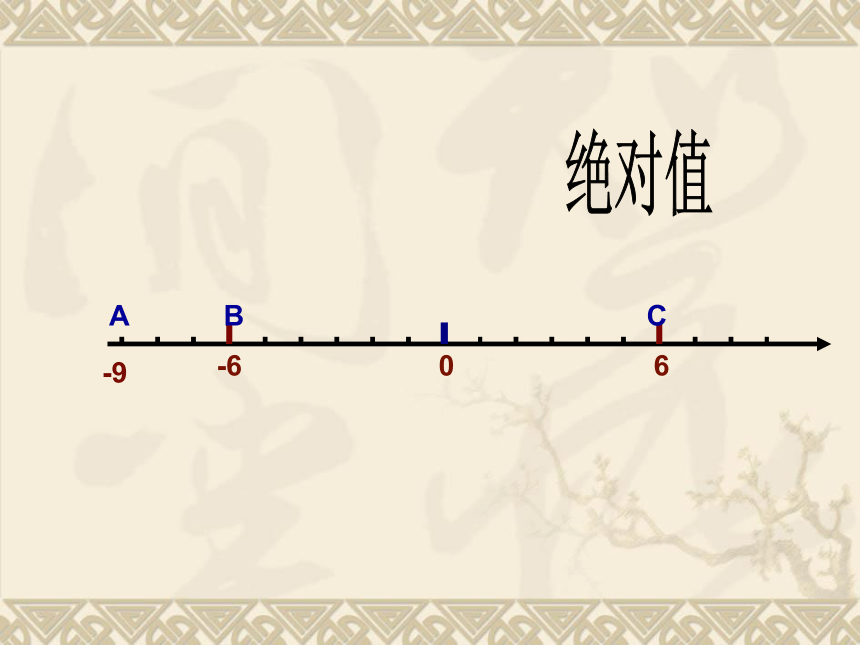
绝 对 值
说课流程图
教材分析
目标分析
教法分析
过程分析
评价分析
情境引入
探究新知
例题讲解
巩固提高
课堂小结
布置作业
教材分析
1. 教材的编写思路、地位和作用。
(有了接受相关知识的基础,为有理数运算做铺垫,起到承上启下作用)
2. 教学内容。
(绝对值的概念和意义,求一个数的绝对值)
3. 重点:绝对值的意义,求一个数的绝对值。
难点:绝对值的概念,绝对值的意义。
目标分析
1. 认知目标:理解绝对值的概念,掌握绝对值的意 义,会求一个数的绝对值。
2. 能力目标:注意让学生养成主动探究、获取知识 的习惯,培养分析、解决问题的能力,培养发散思维,渗透数形结合、分类讨论的数学思想方法。
3. 情感目标:体会数学与人类的密切联系,了解数学的价值,触发学生学好数学的愿望。
教法分析
1.兴趣引导、启发思考、分组讨论和共同探究的方法。
2.充分利用多媒体教学手段,加强直观教学,增大思维密度,有力的突出重点,突破难点。
3.教给学生从“特殊——一般——特殊”的研究问题、学习知识的方法。
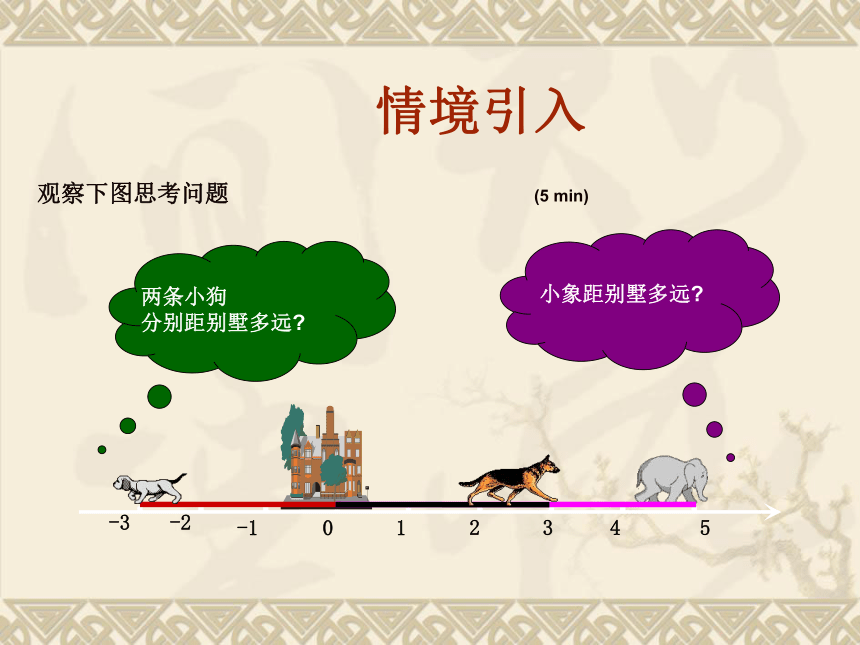
情境引入
观察下图思考问题 (5 min)
0
1
2
3
4
-1
-2
-3
5
两条小狗
分别距别墅多远
小象距别墅多远
B
C
-6
6
0
A
-9
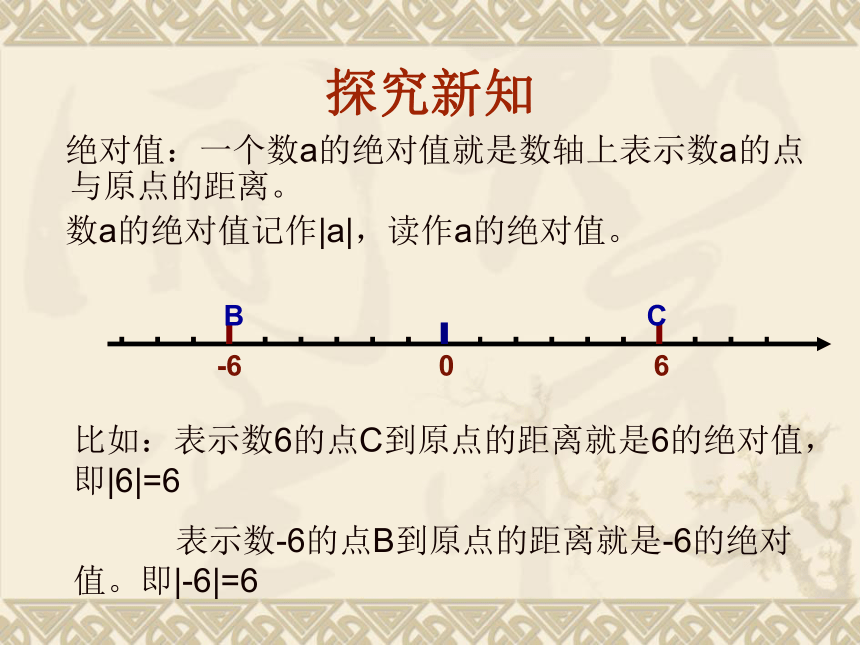
探究新知
绝对值:一个数a的绝对值就是数轴上表示数a的点与原点的距离。
数a的绝对值记作|a|,读作a的绝对值。
B
C
-6
6
0
比如:表示数6的点C到原点的距离就是6的绝对值,即|6|=6
表示数-6的点B到原点的距离就是-6的绝对值。即|-6|=6
探究新知
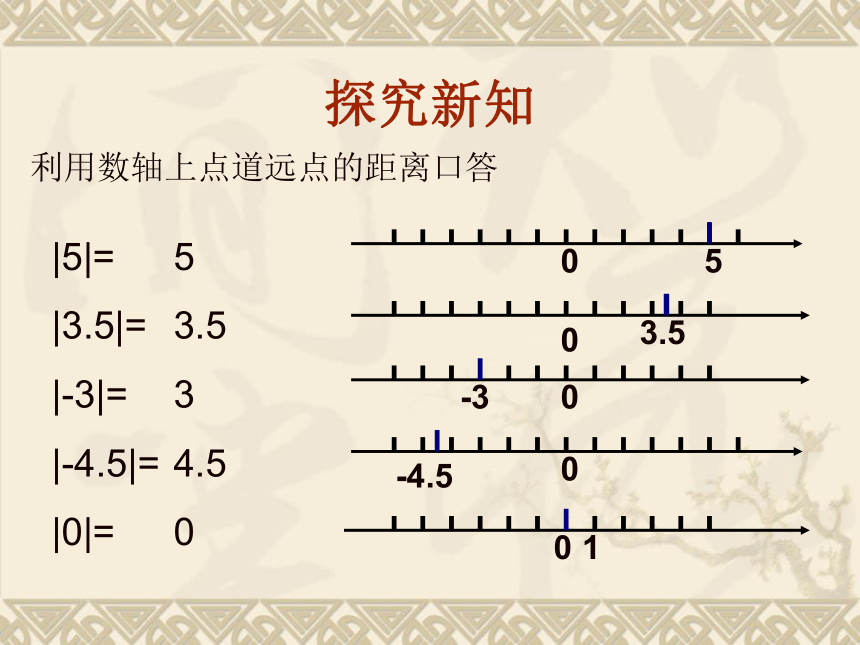
利用数轴上点道远点的距离口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
0
0
0
0
5
3.5
-3
-4.5
1
5
3.5
3
4.5
0
探究新知
|5|=5 |-10|=10
|3.5|= 3.5 |100|=100
|-3|=3 |50|=50
|-4.5|=4.5 |-5000|=5000
|0|=0 …..
思考问题: 一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么? (5min)
探究新知
结论一:一个正数的绝对值是正数。
一个负数的绝对值是正数。
0的绝对值是0。
结论二:一个正数的绝对值是它本身。
一个负数的绝对值是它的相反数。
0的绝对值是0。
探究新知
绝对值的意义:一个正数的绝对值是它本身。
即如果a>0,则|a| =a
一个负数的绝对值是它的相反数。
即如果a<0,则|a| =-a
0的绝对值是0。
即如果a=0,则|a| =0
|a|=
a (a>0)
0 (a=0)
-a (a<0)
即:
注意
|a|≥0
例题讲解
例一: 求下列格式的绝对值
; -3 ; 5-10
解:
=
; |-3|=3
|5-10|= |-5|= |5|
或 |5-10|=10-5=5
例题讲解
例二: 已知一个数的绝对值为 1.5,求这个数。
分析: 如图因为数轴上到原点的距离等于1.5的点有M、N两点。
所以绝对值为1.5的数是1.5或-1.5
0
1.5
-1.5
即: |-1.5|=1.5 |1.5|=1.5
绝对值等于一个正数的数有两个,它们互为相反数
巩固提高
形成性练习: (5min)
1. 求下列个数的绝对值: -5,3,2.3,100,-2,
-0.75,0.5
2. 由|X|=3,甲算出|X|=3,乙算出|X|=-3,请问这两位同学的答案正确吗?
巩固提高
思考题 (实际运用) : (5min)
某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.002L误差.现抽查4瓶食用调和油,超过规定净含量的升数记作正数,不足规定净含量的升数记作负数.检查结果如下表:
-0.0023 +0.0025 -0.0015 +0.0010
请用绝对值知识说明:
(1)哪几瓶是合乎要求的(即在误差范围内的)
(2)哪一瓶净含量最接近规定的净含量
课堂小结
1.绝对值的概念
2.绝对值的意义
作业布置
课外作业:
1.基础题:若|m-1|=m-1,则m_______1 ,
若|m-1|>m-1,则m_______1.
2.拓展题:如果|a|=4, |b|=3,且a绝对值(第一课时)
绝对值的概念:
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
数a的绝对值记作|a|,读作a的绝对值。
绝对值的意义:
一个正数的绝对值是它本身。
即如果a>0,则|a| =a
一个负数的绝对值是它的相反数。
即如果a<0,则|a| =a
0的绝对值是0。
即如果a=0,则|a| =a
|a|=
a (a>0)
0 (a=0)
-a (a<0)
绝对值等于一个正数的数有两个,它们互为相反数
小结:
1.绝对值的概念
2.绝对值的意义
性质:|a|≥0
板书设计
评价分析
这是一堂融知识传授、能力培养和思维训练为一体的课,它遵循了建构主义原则,体现了多元智能理论和差异性发展原理。
分析、解决
问题的能力
数学情感
教学活动
数形结合
分类讨论
培养
渗透
发散思维
数学价值
训练
认识
绝 对 值
说课流程图
教材分析
目标分析
教法分析
过程分析
评价分析
情境引入
探究新知
例题讲解
巩固提高
课堂小结
布置作业
教材分析
1. 教材的编写思路、地位和作用。
(有了接受相关知识的基础,为有理数运算做铺垫,起到承上启下作用)
2. 教学内容。
(绝对值的概念和意义,求一个数的绝对值)
3. 重点:绝对值的意义,求一个数的绝对值。
难点:绝对值的概念,绝对值的意义。
目标分析
1. 认知目标:理解绝对值的概念,掌握绝对值的意 义,会求一个数的绝对值。
2. 能力目标:注意让学生养成主动探究、获取知识 的习惯,培养分析、解决问题的能力,培养发散思维,渗透数形结合、分类讨论的数学思想方法。
3. 情感目标:体会数学与人类的密切联系,了解数学的价值,触发学生学好数学的愿望。
教法分析
1.兴趣引导、启发思考、分组讨论和共同探究的方法。
2.充分利用多媒体教学手段,加强直观教学,增大思维密度,有力的突出重点,突破难点。
3.教给学生从“特殊——一般——特殊”的研究问题、学习知识的方法。
情境引入
观察下图思考问题 (5 min)
0
1
2
3
4
-1
-2
-3
5
两条小狗
分别距别墅多远
小象距别墅多远
B
C
-6
6
0
A
-9
探究新知
绝对值:一个数a的绝对值就是数轴上表示数a的点与原点的距离。
数a的绝对值记作|a|,读作a的绝对值。
B
C
-6
6
0
比如:表示数6的点C到原点的距离就是6的绝对值,即|6|=6
表示数-6的点B到原点的距离就是-6的绝对值。即|-6|=6
探究新知
利用数轴上点道远点的距离口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
0
0
0
0
5
3.5
-3
-4.5
1
5
3.5
3
4.5
0
探究新知
|5|=5 |-10|=10
|3.5|= 3.5 |100|=100
|-3|=3 |50|=50
|-4.5|=4.5 |-5000|=5000
|0|=0 …..
思考问题: 一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么? (5min)
探究新知
结论一:一个正数的绝对值是正数。
一个负数的绝对值是正数。
0的绝对值是0。
结论二:一个正数的绝对值是它本身。
一个负数的绝对值是它的相反数。
0的绝对值是0。
探究新知
绝对值的意义:一个正数的绝对值是它本身。
即如果a>0,则|a| =a
一个负数的绝对值是它的相反数。
即如果a<0,则|a| =-a
0的绝对值是0。
即如果a=0,则|a| =0
|a|=
a (a>0)
0 (a=0)
-a (a<0)
即:
注意
|a|≥0
例题讲解
例一: 求下列格式的绝对值
; -3 ; 5-10
解:
=
; |-3|=3
|5-10|= |-5|= |5|
或 |5-10|=10-5=5
例题讲解
例二: 已知一个数的绝对值为 1.5,求这个数。
分析: 如图因为数轴上到原点的距离等于1.5的点有M、N两点。
所以绝对值为1.5的数是1.5或-1.5
0
1.5
-1.5
即: |-1.5|=1.5 |1.5|=1.5
绝对值等于一个正数的数有两个,它们互为相反数
巩固提高
形成性练习: (5min)
1. 求下列个数的绝对值: -5,3,2.3,100,-2,
-0.75,0.5
2. 由|X|=3,甲算出|X|=3,乙算出|X|=-3,请问这两位同学的答案正确吗?
巩固提高
思考题 (实际运用) : (5min)
某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.002L误差.现抽查4瓶食用调和油,超过规定净含量的升数记作正数,不足规定净含量的升数记作负数.检查结果如下表:
-0.0023 +0.0025 -0.0015 +0.0010
请用绝对值知识说明:
(1)哪几瓶是合乎要求的(即在误差范围内的)
(2)哪一瓶净含量最接近规定的净含量
课堂小结
1.绝对值的概念
2.绝对值的意义
作业布置
课外作业:
1.基础题:若|m-1|=m-1,则m_______1 ,
若|m-1|>m-1,则m_______1.
2.拓展题:如果|a|=4, |b|=3,且a
绝对值的概念:
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
数a的绝对值记作|a|,读作a的绝对值。
绝对值的意义:
一个正数的绝对值是它本身。
即如果a>0,则|a| =a
一个负数的绝对值是它的相反数。
即如果a<0,则|a| =a
0的绝对值是0。
即如果a=0,则|a| =a
|a|=
a (a>0)
0 (a=0)
-a (a<0)
绝对值等于一个正数的数有两个,它们互为相反数
小结:
1.绝对值的概念
2.绝对值的意义
性质:|a|≥0
板书设计
评价分析
这是一堂融知识传授、能力培养和思维训练为一体的课,它遵循了建构主义原则,体现了多元智能理论和差异性发展原理。
分析、解决
问题的能力
数学情感
教学活动
数形结合
分类讨论
培养
渗透
发散思维
数学价值
训练
认识
