垂径定理[上学期]
图片预览




文档简介
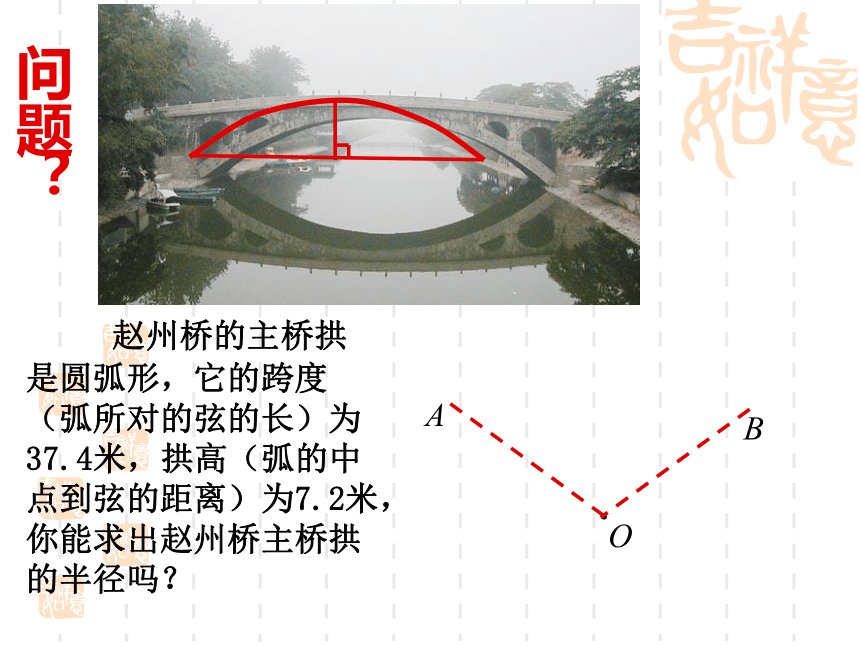
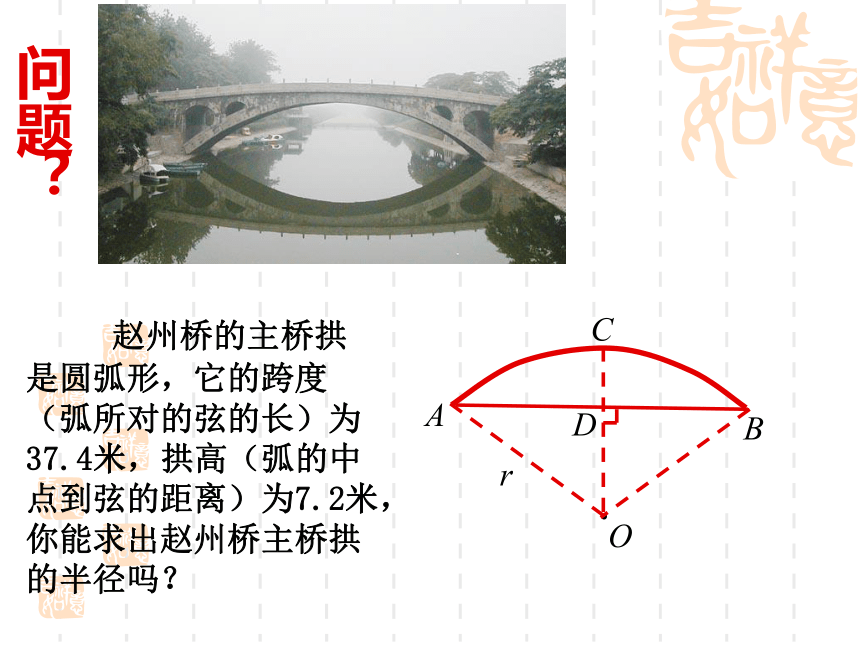
课件33张PPT。24.1.2 垂直于弦的直径实验中学 苑洪申 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?问题?OAB1.若将一等腰三角形沿着底边上的高对折, 将会发生什么?2.如果以这个等腰三角形的顶点为圆心,腰长为半径作圆,得到的圆是否是轴对称图形呢?结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴.强调:
(1)对称轴是直线,不能说每一条直径都是它的对称轴;
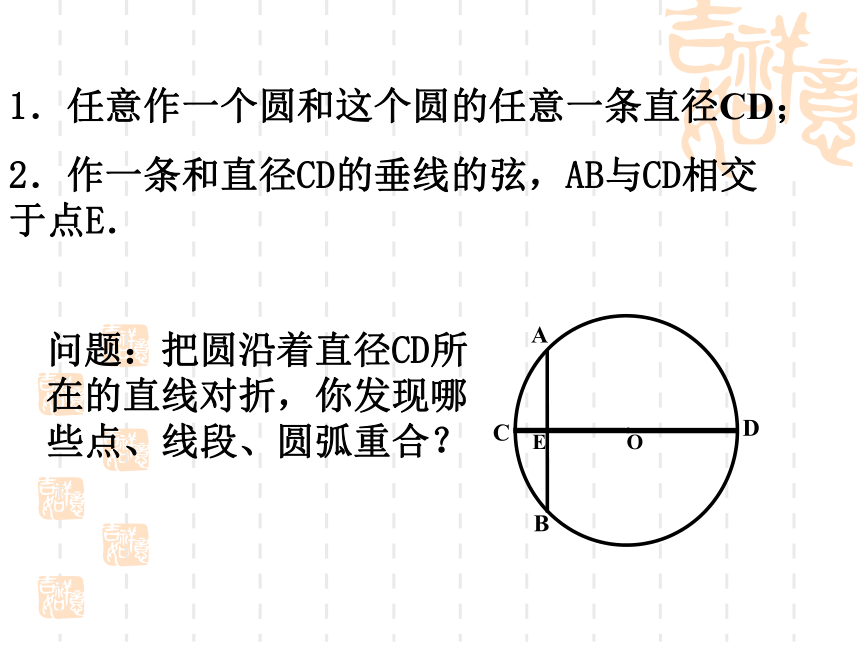
(2)圆的对称轴有无数条.判断:任意一条直径都是圆的对称轴( )1.任意作一个圆和这个圆的任意一条直径CD;
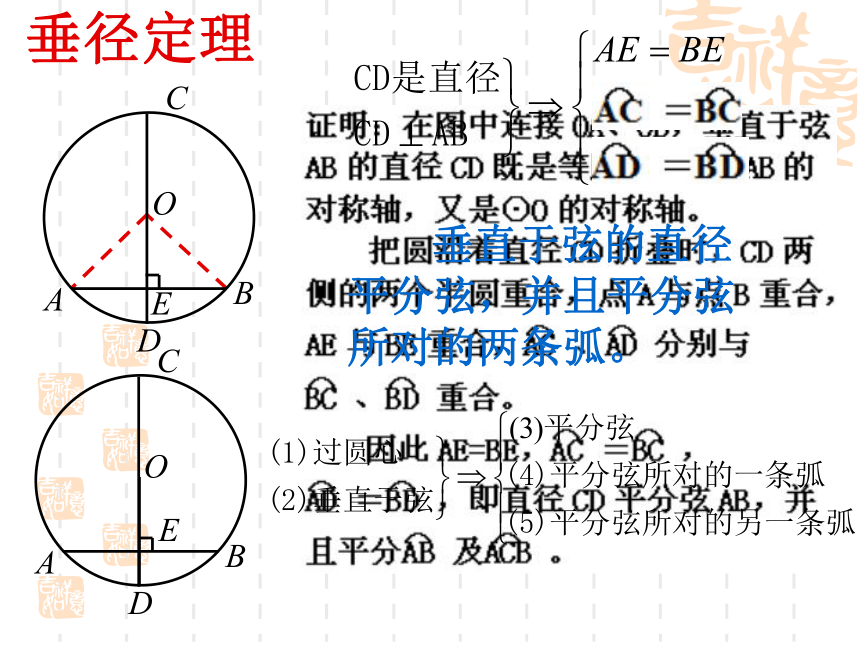
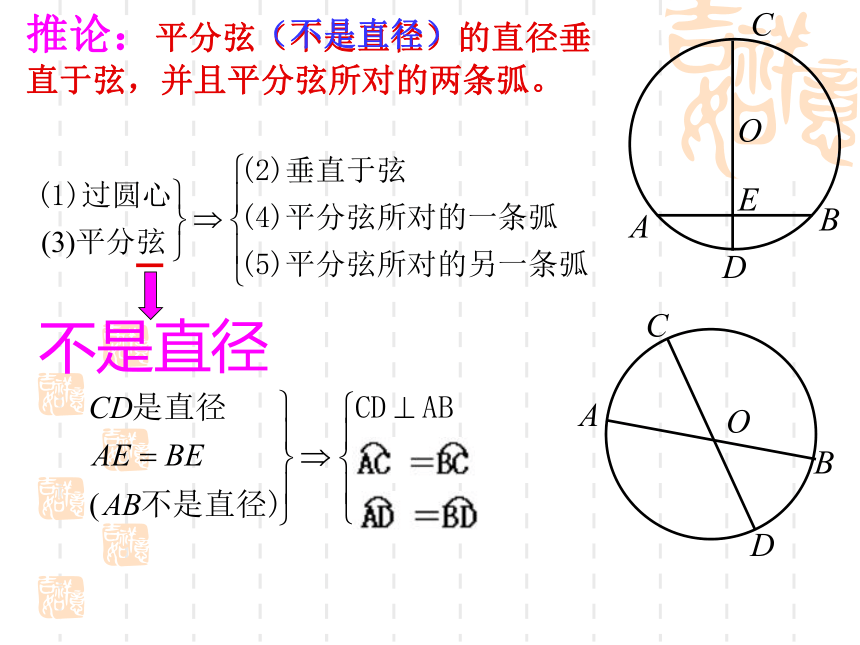
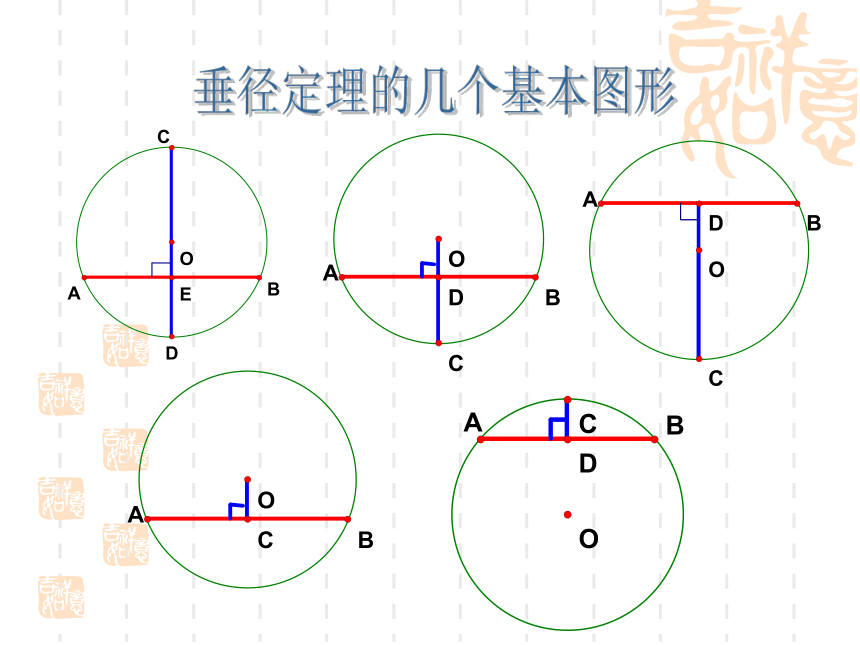
2.作一条和直径CD的垂线的弦,AB与CD相交于点E.问题:把圆沿着直径CD所在的直线对折,你发现哪些点、线段、圆弧重合?ABCDOE 垂直于弦的直径平分弦,并且平分弦所对的两条弧。垂径定理BAOCDEBAOCDE不是直径 推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 BAOCDE(不是直径)垂径定理的几个基本图形(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )(4)圆内两条非直径的弦不能互相平分( )×√×√ODCBA弓形的弦AB=8
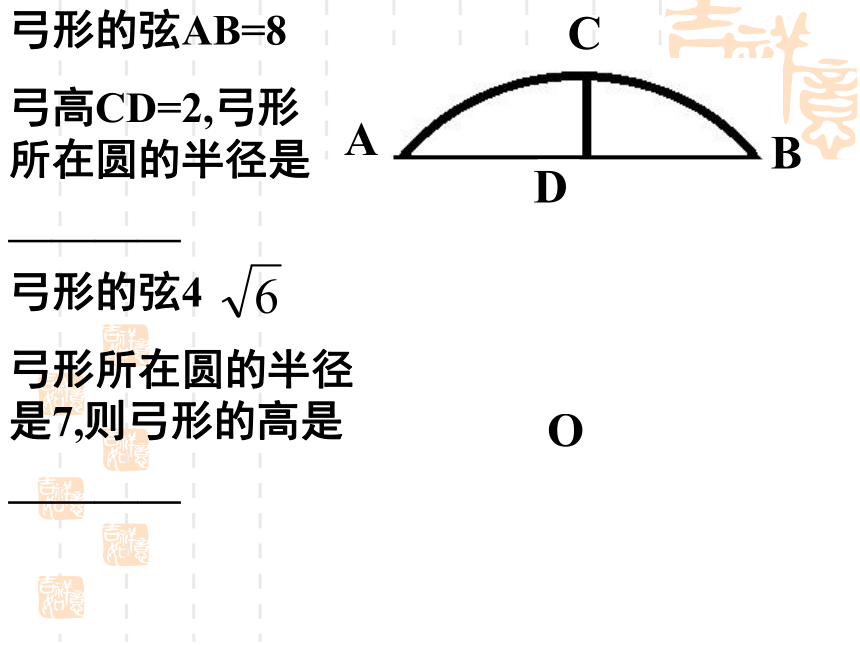
弓高CD=2,弓形所在圆的半径是
————弓形的弦4
弓形所在圆的半径是7,则弓形的高是
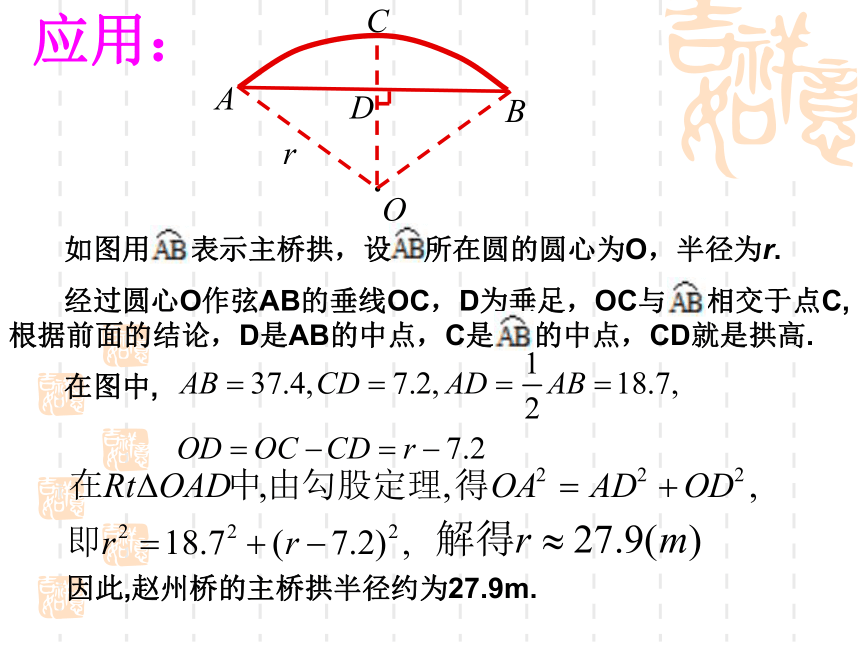
———— 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?问题?OABr应用:因此,赵州桥的主桥拱半径约为27.9m.应用:已知如图,在 ⊙O 中,弦AB的长为8cm,若圆心O到AB的距离为3 cm,则⊙O 的半径为 cm.
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 51、同心圆O中,大圆的直径AB交小圆于点C、D,请问AC=BD吗?
2、如果把AB向下平移,弦AB仍然交小圆于点C、D,此时图中还有哪些相等的线段?为什么?应用:1在圆中研究有关弦的问题时,常过圆心作垂直于弦的垂线段,利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算. 例3 已知:如图,线段AB与⊙O交于C、D两点,且OA=OB .求证:AC=BD ..OABCMD练2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。ABCDOE练习:在圆O中,直径CE⊥AB于
D,OD=4 ㎝,弦AC= ㎝ ,
求圆O的半径。
ABCDEO例2如图,一条排水管的截面。已知排水管的半径10cm,水面宽AB=12cm。求水的最大深度. 若水面又上升1厘米,求此时水面的宽度练习:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。ABCDEO练3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
ABCDOEFGABCO 一矩形和
⊙O交于如图,
AB=4,BC=5,DE=3
求EF的长
NMFDEABCO 一矩形和
⊙O交于如图,
AB 是⊙O的直径
AB=10,EF=8
求AC的长
MFDEABEO 1.⊙O弦AB⊥CD
于E,AE=2,BE=6
ED=3,EC=4
求 ⊙O的半径
MNDC提高练习归纳小结你学习了哪些内容?
你有哪些收获?
你掌握了哪些思想方法?
你还有什么问题 ?作法:⒈ 连结AB.⒉作AB的垂直平分线 CD, 交弧AB于点E.点E就是所求弧AB的中点.CDABE变式一: 求弧AB的四等分点.CDABEFGmn变式一: 求弧AB的四等分点.CDABMFG错在哪里?1.作AB的垂直平分线CD2.作AT、BT的垂直平分线EF、GHTENHP强调:等分弧时一定要作弧所对的弦的垂直平分线.变式二:你能确定弧AB的圆心吗?OABC ab方法:只要在圆弧上任意取三点,得到三条弦,画其中两条弦的垂直平分线,交点即为圆弧的圆心.你能找到原来车轮的圆心吗?挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.PO
⊙O的半径是2,
P是⊙O内的一点,
OP=1,过P的最长的
弦=___,过P的最短
的弦=___
BA2.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3
圆是轴对称图形,每一条直径所在的直线都是对称轴.强调:
(1)对称轴是直线,不能说每一条直径都是它的对称轴;
(2)圆的对称轴有无数条.判断:任意一条直径都是圆的对称轴( )1.任意作一个圆和这个圆的任意一条直径CD;
2.作一条和直径CD的垂线的弦,AB与CD相交于点E.问题:把圆沿着直径CD所在的直线对折,你发现哪些点、线段、圆弧重合?ABCDOE 垂直于弦的直径平分弦,并且平分弦所对的两条弧。垂径定理BAOCDEBAOCDE不是直径 推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 BAOCDE(不是直径)垂径定理的几个基本图形(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )(4)圆内两条非直径的弦不能互相平分( )×√×√ODCBA弓形的弦AB=8
弓高CD=2,弓形所在圆的半径是
————弓形的弦4
弓形所在圆的半径是7,则弓形的高是
———— 赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?问题?OABr应用:因此,赵州桥的主桥拱半径约为27.9m.应用:已知如图,在 ⊙O 中,弦AB的长为8cm,若圆心O到AB的距离为3 cm,则⊙O 的半径为 cm.
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 51、同心圆O中,大圆的直径AB交小圆于点C、D,请问AC=BD吗?
2、如果把AB向下平移,弦AB仍然交小圆于点C、D,此时图中还有哪些相等的线段?为什么?应用:1在圆中研究有关弦的问题时,常过圆心作垂直于弦的垂线段,利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算. 例3 已知:如图,线段AB与⊙O交于C、D两点,且OA=OB .求证:AC=BD ..OABCMD练2:如图,圆O的弦AB=8 ㎝ ,
DC=2㎝,直径CE⊥AB于D,
求半径OC的长。ABCDOE练习:在圆O中,直径CE⊥AB于
D,OD=4 ㎝,弦AC= ㎝ ,
求圆O的半径。
ABCDEO例2如图,一条排水管的截面。已知排水管的半径10cm,水面宽AB=12cm。求水的最大深度. 若水面又上升1厘米,求此时水面的宽度练习:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。ABCDEO练3:如图,已知圆O的直径AB与
弦CD相交于G,AE⊥CD于E,
BF⊥CD于F,且圆O的半径为
10㎝,CD=16 ㎝,求AE-BF的长。
ABCDOEFGABCO 一矩形和
⊙O交于如图,
AB=4,BC=5,DE=3
求EF的长
NMFDEABCO 一矩形和
⊙O交于如图,
AB 是⊙O的直径
AB=10,EF=8
求AC的长
MFDEABEO 1.⊙O弦AB⊥CD
于E,AE=2,BE=6
ED=3,EC=4
求 ⊙O的半径
MNDC提高练习归纳小结你学习了哪些内容?
你有哪些收获?
你掌握了哪些思想方法?
你还有什么问题 ?作法:⒈ 连结AB.⒉作AB的垂直平分线 CD, 交弧AB于点E.点E就是所求弧AB的中点.CDABE变式一: 求弧AB的四等分点.CDABEFGmn变式一: 求弧AB的四等分点.CDABMFG错在哪里?1.作AB的垂直平分线CD2.作AT、BT的垂直平分线EF、GHTENHP强调:等分弧时一定要作弧所对的弦的垂直平分线.变式二:你能确定弧AB的圆心吗?OABC ab方法:只要在圆弧上任意取三点,得到三条弦,画其中两条弦的垂直平分线,交点即为圆弧的圆心.你能找到原来车轮的圆心吗?挑战自我画一画如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.PO
⊙O的半径是2,
P是⊙O内的一点,
OP=1,过P的最长的
弦=___,过P的最短
的弦=___
BA2.如图,⊙O的直径为10,弦AB长为8,M是弦AB上的动点,则OM的长的取值范围是( )
A.3≤OM≤5 B.4≤OM≤5
C.3
同课章节目录
