辽宁省葫芦岛市连山区2022-2023学年九年级下学期期末数学试题(含答案)
文档属性
| 名称 | 辽宁省葫芦岛市连山区2022-2023学年九年级下学期期末数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-06 17:09:20 | ||
图片预览


文档简介
2022-2023学年度第一学期连山区九年级期末考试
数学试卷
※考试时间120分钟 满分为150分
考生注意:请在答题卡各题目规定答题区内作答,答在本试卷上无效
第一部分 选择题(共30分)
一、选择题(本题共10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若关于的一元二次方程有两个相等的实数根,则的值是( )
A. B.1 C.0 D.2
2.关于抛物线图象的性质,下列说法错误的是( )
A.开口向下 B.对称轴 C.顶点坐标是 D.与轴没有交点
3.下列四个有关环保的图形中,是轴对称图形,但不是中心对称图形的是( )
A. B.
C. D.
4.如图,是的直径,与相切于点的延长线交于点,则的度数是( )
A. B. C. D.
5.下列事件属于必然事件的是( )
A.掷一枚质地均匀的骰子,掷出的点数是奇数
B.车辆随机经过一个路口,遇到红灯
C.任意画一个三角形,其内角和是
D.有三条线段,将这三条线段首尾顺次相接可以组成一个三角形
6.若反比例函数的图象位于第一、三象限,则的取值可以是( )
A. B. C. D.0
7.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )
A. B.
C. D.
8.如图,小球从口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从口落出的概率为( )
A. B. C. D.
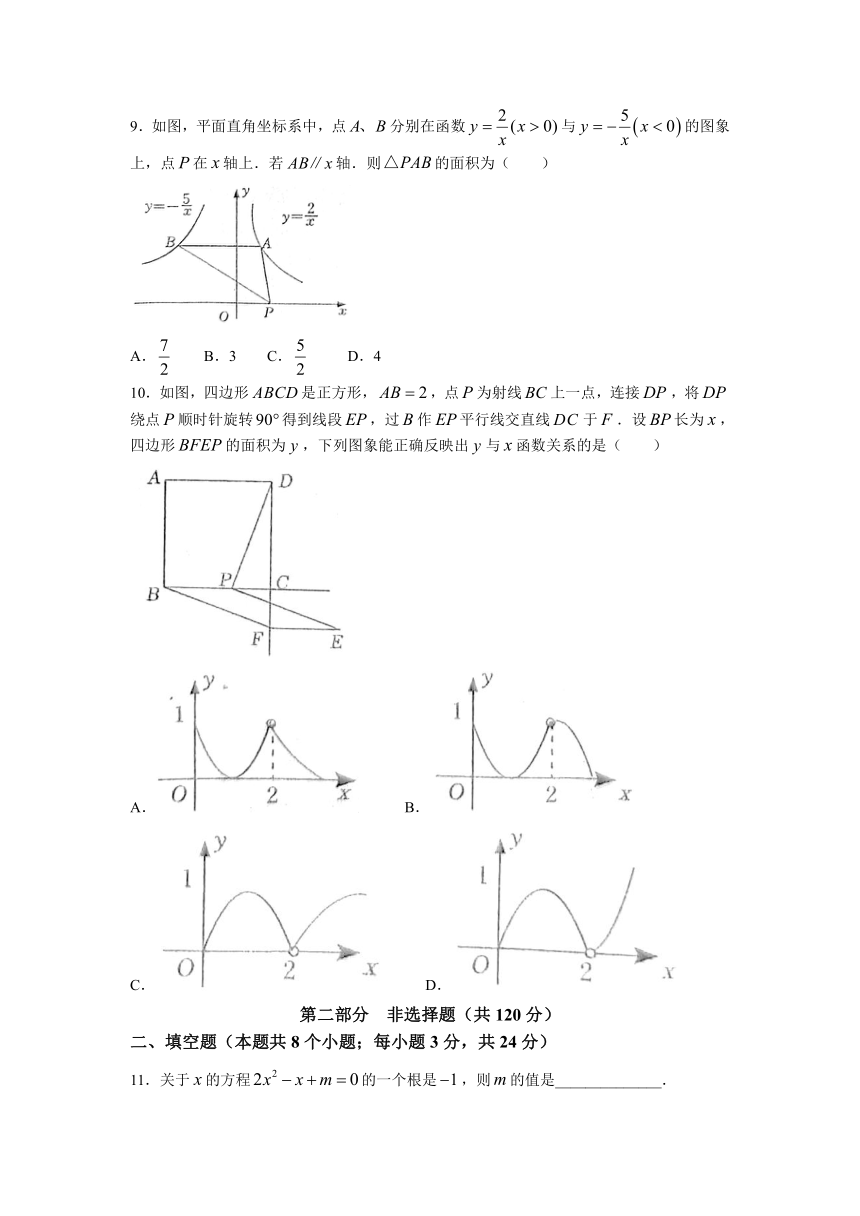
9.如图,平面直角坐标系中,点分别在函数与的图象上,点在轴上.若轴.则的面积为( )
A. B.3 C. D.4
10.如图,四边形是正方形,,点为射线上一点,连接,将绕点顺时针旋转得到线段,过作平行线交直线于.设长为,四边形的面积为,下列图象能正确反映出与函数关系的是( )
A. B.
C. D.
第二部分 非选择题(共120分)
二、填空题(本题共8个小题;每小题3分,共24分)
11.关于的方程的一个根是,则的值是______________.
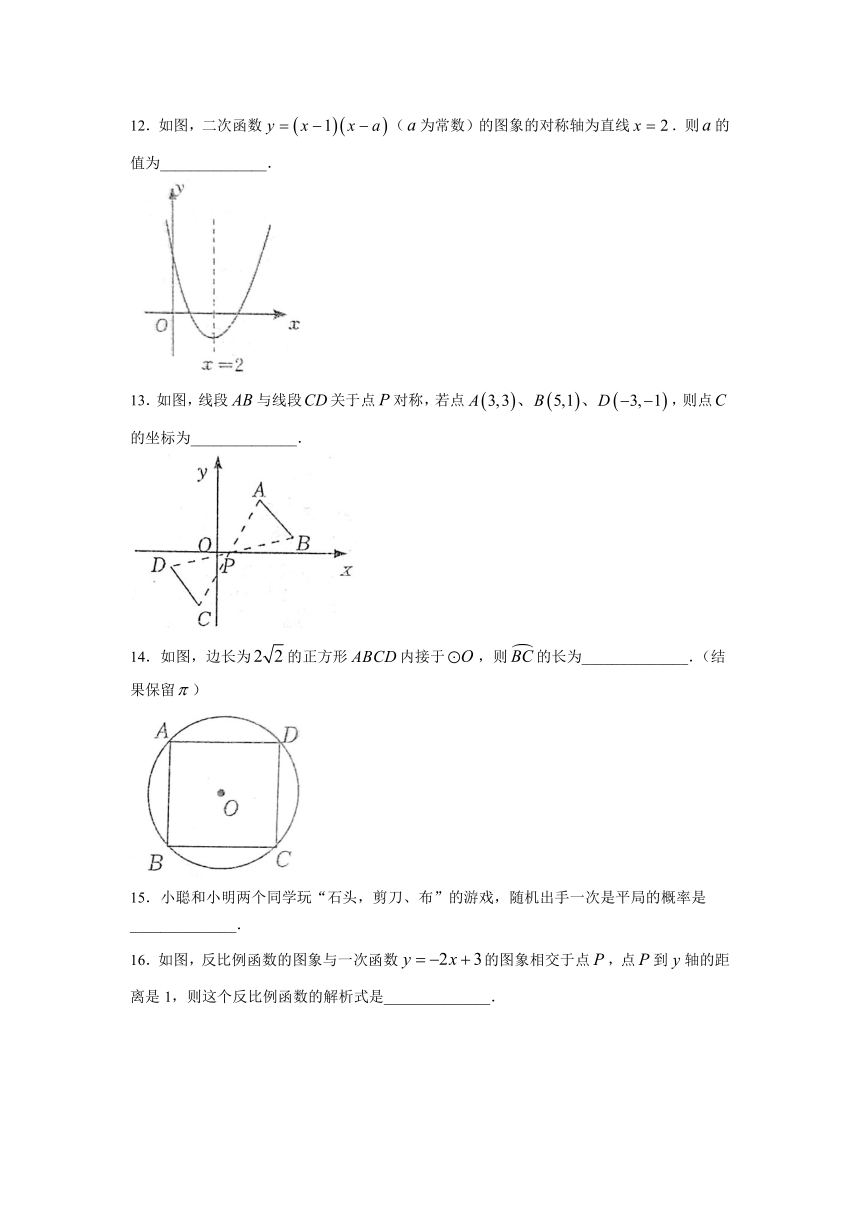
12.如图,二次函数(为常数)的图象的对称轴为直线.则的值为______________.
13.如图,线段与线段关于点对称,若点,则点的坐标为______________.
14.如图,边长为的正方形内接于,则的长为______________.(结果保留)
15.小聪和小明两个同学玩“石头,剪刀、布”的游戏,随机出手一次是平局的概率是______________.
16.如图,反比例函数的图象与一次函数的图象相交于点,点到轴的距离是1,则这个反比例函数的解析式是______________.
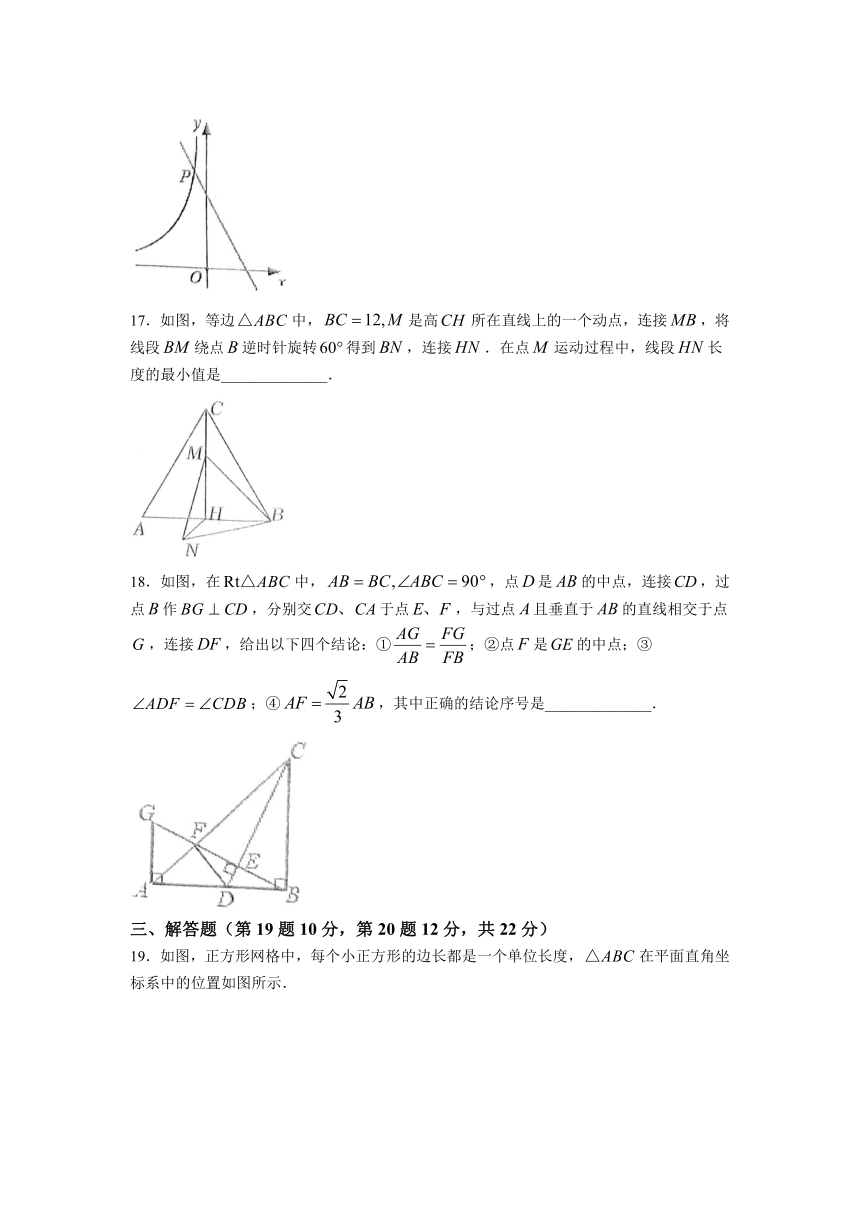
17.如图,等边中,是高所在直线上的一个动点,连接,将线段绕点逆时针旋转得到,连接.在点运动过程中,线段长度的最小值是______________.
18.如图,在中,,点是的中点,连接,过点作,分别交于点,与过点且垂直于的直线相交于点,连接,给出以下四个结论:①;②点是的中点;③;④,其中正确的结论序号是______________.
三、解答题(第19题10分,第20题12分,共22分)
19.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中的位置如图所示.
(1)画出关于轴对称的;
(2)画出将绕点顺时针方向旋转得到的;
(3)在(2)的旋转变换中,请直接写出线段扫过的面积.
20.在桌面上放有三张完全相同的卡片,其正面分别写有数字,1,把这三张卡片背面朝上洗匀放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取一张卡片,其上的数字记为,然后放回并洗匀,再随机抽取一张卡片,其上的数字记为,用列表或画树状图的方法求出点在双曲线上的概率.
四.解答题(第21题12分,第22题12分,共24分)
21.如图,是矩形的边上的一点,于点.
(1)求证:;
(2)若,当点为中点时,求线段的长度.
22.如图,点和点在反比例函数的图象上,过点作轴交轴于点,过点作轴交直线于点.
(1)若,求的值.
(2)过点作轴于点,若四边形的面积为8,求点的坐标.
五.解答题(满分12分)
23.某景区超市销售一种纪念品,这种商品的成本价14元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于24元/件,市场调查发现,该商品每天的销售量(件)与销售单价(元/件).之间的函数关系如图所示.
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)求每天的销售利润(元)与销售单价(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
六.解答题(满分12分)
24.如图,在中,,点为边的中点,以为直径作,分别与,交于点,过点作于.
(1)求证:是的切线;
(2)若的半径为5,求的长.
七.解答题(满分12分)
25.正方形,点在直线上,连接,将射线绕点顺时针旋转得到射线,射线与直线交于点.
(1)当点在边上时,如图1,直接写出与的数量关系;
(2)如图2,当点在线段上,点在的延长线上时,(1)中的结论还成立吗?若成立请说明理由;若不成立,请写出正确的结论,并说明理由;
(3)若,当时,请直接写出的面积值.
八.解答题(满分14分)
26.如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于点.
(1)求拋物线的函数解析式;
(2)如图1,点为直线下方抛物线上一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,过点作轴的平行线交轴于点,得到矩形,求矩形的周长最大值及此时点的坐标;
(3)点是直线上一动点,点是在平面内一点,当以点为顶点的四边形是菱形时,请直接写出点的坐标.(参考数据:)
2022--2023学年度上学期九年级数学期末考试参考答案
一、BDCAC DBCAD
二、11. 12.3 13. 14.略 15. 16. 17.3 18.①③④
三.19.(1)如图,为所作;
(2)如图,为所作;
(3)线段扫过的面积为.
20.(1)三张卡片数字中有2个负数,
随机的取一张卡片,抽取的卡片上的数字为负数的概率为;
(2)画树状图如图所示:
由树状图可知:共有9种结果,每种结果出现的可能性相同,其中点在反比例图象上的结果有2个,
点在反比例图象上的概率为.
21.(1)证明:四边形是矩形,
,
,
,
,
又,
;
(2)四边形是矩形,
.
点为中点,
.
由(1)知:,
,即,
,
.
(1)点,
又,
轴,点,
点和点都在反比例函数图象上
,
点;
(2)四边形的面积为8,
点,
点和点都在反比例函数图象上
,
点.
数学试卷
※考试时间120分钟 满分为150分
考生注意:请在答题卡各题目规定答题区内作答,答在本试卷上无效
第一部分 选择题(共30分)
一、选择题(本题共10个小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若关于的一元二次方程有两个相等的实数根,则的值是( )
A. B.1 C.0 D.2
2.关于抛物线图象的性质,下列说法错误的是( )
A.开口向下 B.对称轴 C.顶点坐标是 D.与轴没有交点
3.下列四个有关环保的图形中,是轴对称图形,但不是中心对称图形的是( )
A. B.
C. D.
4.如图,是的直径,与相切于点的延长线交于点,则的度数是( )
A. B. C. D.
5.下列事件属于必然事件的是( )
A.掷一枚质地均匀的骰子,掷出的点数是奇数
B.车辆随机经过一个路口,遇到红灯
C.任意画一个三角形,其内角和是
D.有三条线段,将这三条线段首尾顺次相接可以组成一个三角形
6.若反比例函数的图象位于第一、三象限,则的取值可以是( )
A. B. C. D.0
7.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )
A. B.
C. D.
8.如图,小球从口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从口落出的概率为( )
A. B. C. D.
9.如图,平面直角坐标系中,点分别在函数与的图象上,点在轴上.若轴.则的面积为( )
A. B.3 C. D.4
10.如图,四边形是正方形,,点为射线上一点,连接,将绕点顺时针旋转得到线段,过作平行线交直线于.设长为,四边形的面积为,下列图象能正确反映出与函数关系的是( )
A. B.
C. D.
第二部分 非选择题(共120分)
二、填空题(本题共8个小题;每小题3分,共24分)
11.关于的方程的一个根是,则的值是______________.
12.如图,二次函数(为常数)的图象的对称轴为直线.则的值为______________.
13.如图,线段与线段关于点对称,若点,则点的坐标为______________.
14.如图,边长为的正方形内接于,则的长为______________.(结果保留)
15.小聪和小明两个同学玩“石头,剪刀、布”的游戏,随机出手一次是平局的概率是______________.
16.如图,反比例函数的图象与一次函数的图象相交于点,点到轴的距离是1,则这个反比例函数的解析式是______________.
17.如图,等边中,是高所在直线上的一个动点,连接,将线段绕点逆时针旋转得到,连接.在点运动过程中,线段长度的最小值是______________.
18.如图,在中,,点是的中点,连接,过点作,分别交于点,与过点且垂直于的直线相交于点,连接,给出以下四个结论:①;②点是的中点;③;④,其中正确的结论序号是______________.
三、解答题(第19题10分,第20题12分,共22分)
19.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中的位置如图所示.
(1)画出关于轴对称的;
(2)画出将绕点顺时针方向旋转得到的;
(3)在(2)的旋转变换中,请直接写出线段扫过的面积.
20.在桌面上放有三张完全相同的卡片,其正面分别写有数字,1,把这三张卡片背面朝上洗匀放在桌面上.
(1)随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;
(2)先随机抽取一张卡片,其上的数字记为,然后放回并洗匀,再随机抽取一张卡片,其上的数字记为,用列表或画树状图的方法求出点在双曲线上的概率.
四.解答题(第21题12分,第22题12分,共24分)
21.如图,是矩形的边上的一点,于点.
(1)求证:;
(2)若,当点为中点时,求线段的长度.
22.如图,点和点在反比例函数的图象上,过点作轴交轴于点,过点作轴交直线于点.
(1)若,求的值.
(2)过点作轴于点,若四边形的面积为8,求点的坐标.
五.解答题(满分12分)
23.某景区超市销售一种纪念品,这种商品的成本价14元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于24元/件,市场调查发现,该商品每天的销售量(件)与销售单价(元/件).之间的函数关系如图所示.
(1)求与之间的函数关系式,并写出自变量的取值范围;
(2)求每天的销售利润(元)与销售单价(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
六.解答题(满分12分)
24.如图,在中,,点为边的中点,以为直径作,分别与,交于点,过点作于.
(1)求证:是的切线;
(2)若的半径为5,求的长.
七.解答题(满分12分)
25.正方形,点在直线上,连接,将射线绕点顺时针旋转得到射线,射线与直线交于点.
(1)当点在边上时,如图1,直接写出与的数量关系;
(2)如图2,当点在线段上,点在的延长线上时,(1)中的结论还成立吗?若成立请说明理由;若不成立,请写出正确的结论,并说明理由;
(3)若,当时,请直接写出的面积值.
八.解答题(满分14分)
26.如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于点.
(1)求拋物线的函数解析式;
(2)如图1,点为直线下方抛物线上一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,过点作轴的平行线交轴于点,得到矩形,求矩形的周长最大值及此时点的坐标;
(3)点是直线上一动点,点是在平面内一点,当以点为顶点的四边形是菱形时,请直接写出点的坐标.(参考数据:)
2022--2023学年度上学期九年级数学期末考试参考答案
一、BDCAC DBCAD
二、11. 12.3 13. 14.略 15. 16. 17.3 18.①③④
三.19.(1)如图,为所作;
(2)如图,为所作;
(3)线段扫过的面积为.
20.(1)三张卡片数字中有2个负数,
随机的取一张卡片,抽取的卡片上的数字为负数的概率为;
(2)画树状图如图所示:
由树状图可知:共有9种结果,每种结果出现的可能性相同,其中点在反比例图象上的结果有2个,
点在反比例图象上的概率为.
21.(1)证明:四边形是矩形,
,
,
,
,
又,
;
(2)四边形是矩形,
.
点为中点,
.
由(1)知:,
,即,
,
.
(1)点,
又,
轴,点,
点和点都在反比例函数图象上
,
点;
(2)四边形的面积为8,
点,
点和点都在反比例函数图象上
,
点.
同课章节目录
