24.1.2垂直于弦的直径(2)[上学期]
文档属性
| 名称 | 24.1.2垂直于弦的直径(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-01 00:00:00 | ||
图片预览

文档简介
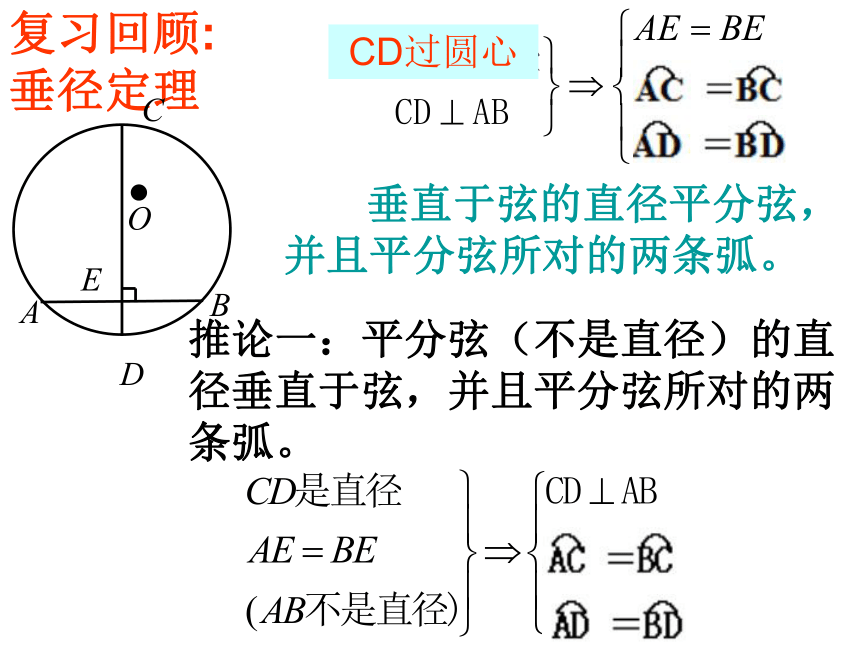
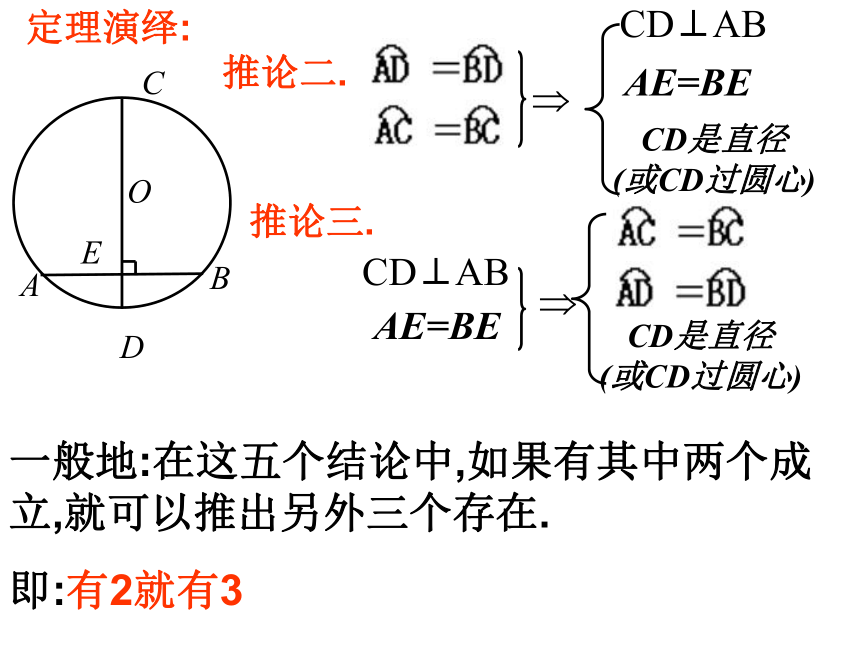
课件15张PPT。24.1.2垂直于弦的直径(二) 垂直于弦的直径平分弦,并且平分弦所对的两条弧。复习回顾:垂径定理CD过圆心推论一:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。 定理演绎:推论二.CD是直径
(或CD过圆心)AE=BETCD⊥ABCD⊥ABAE=BETCD是直径
(或CD过圆心)推论三.一般地:在这五个结论中,如果有其中两个成立,就可以推出另外三个存在.
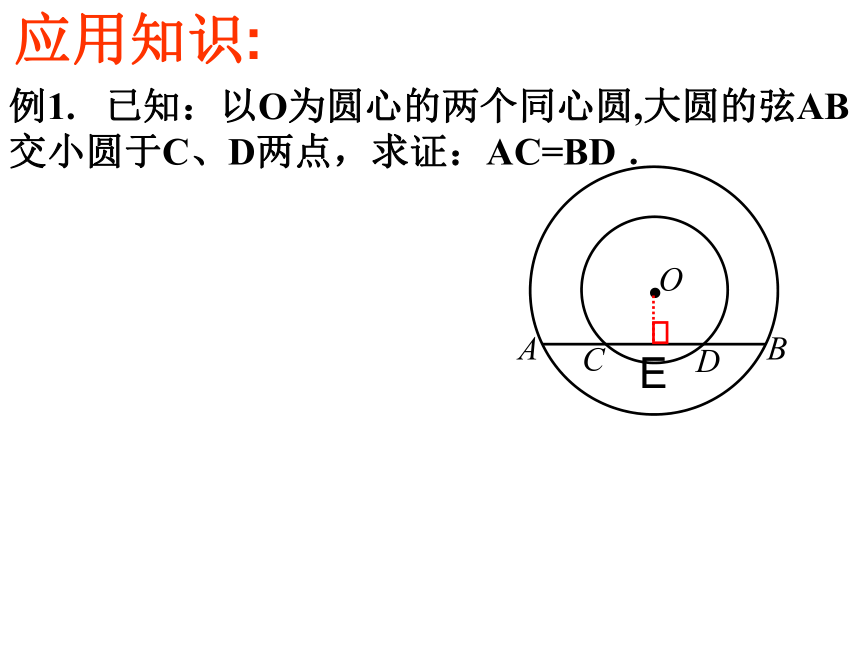
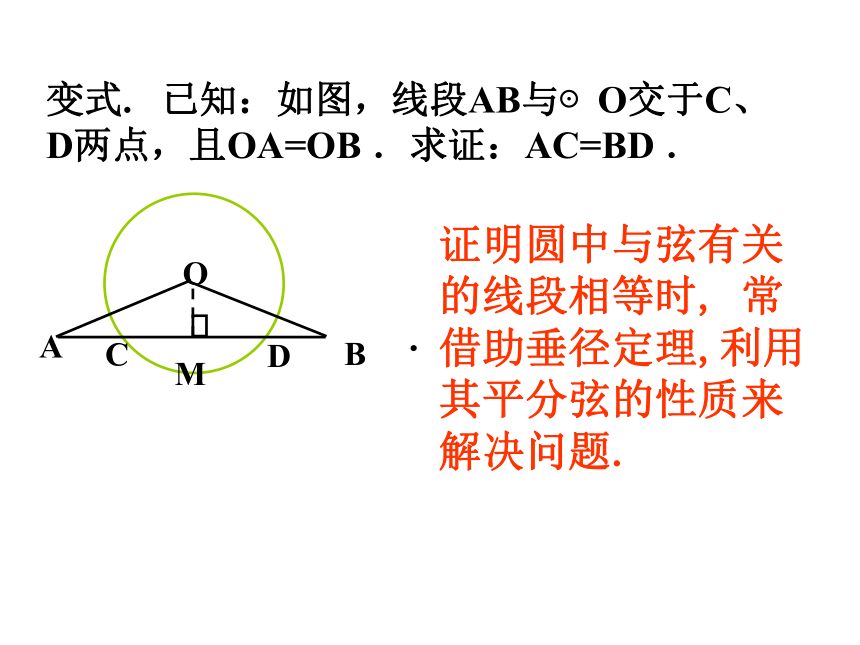
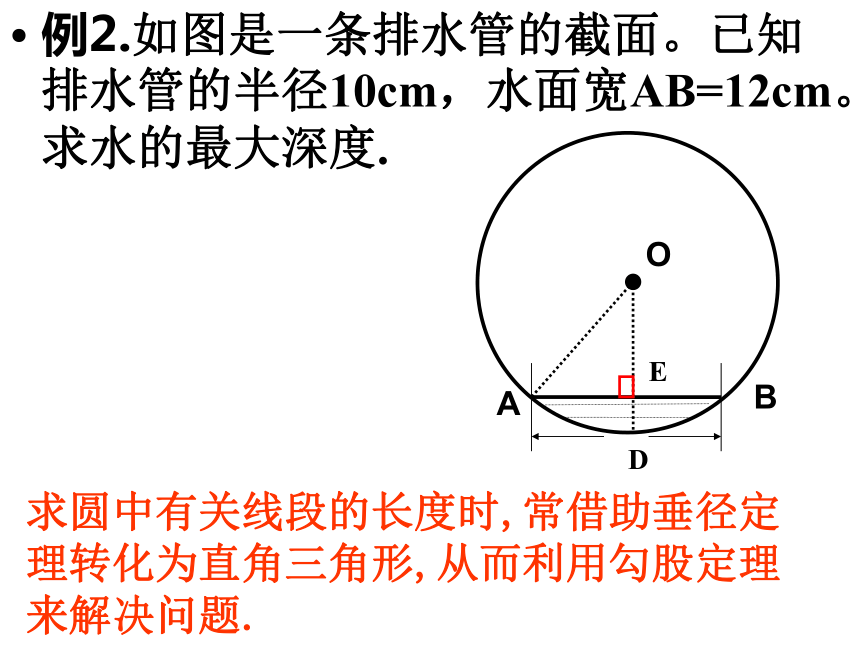
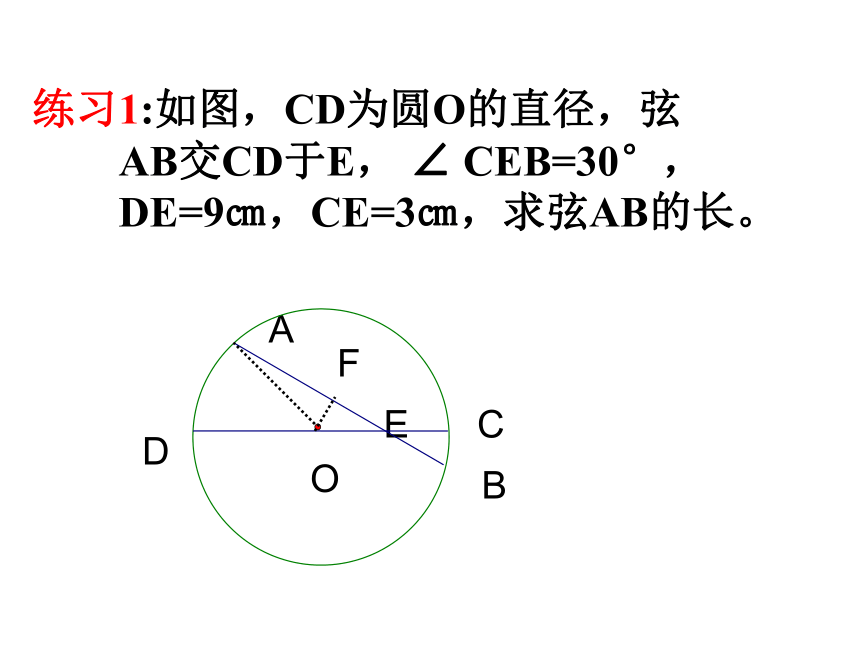
即:有2就有3例1. 已知:以O为圆心的两个同心圆,大圆的弦AB交小圆于C、D两点,求证:AC=BD .应用知识:变式. 已知:如图,线段AB与⊙O交于C、D两点,且OA=OB .求证:AC=BD ..证明圆中与弦有关的线段相等时, 常借助垂径定理,利用其平分弦的性质来解决问题. 例2.如图是一条排水管的截面。已知排水管的半径10cm,水面宽AB=12cm。求水的最大深度. ED求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. BAO练习1:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。O作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点.CDABE依据:变式一: 求弧AB的四等分点.CDABEFGmn弧AB的四等分点的典型错误.CDABMFG错在哪里?1.作AB的垂直平分线CD2.作AT、BT的垂直平分线EF、GHTENHP强调:等分弧时一定要作弧所对的弦的垂直平分线.变式二:你能确定弧AB的圆心吗?OABC ab方法:只要在圆弧上任意取两条弦,画这两条弦的垂直平分线,交点即为圆弧的圆心.变式三.你能找到原来车轮的圆心吗?1. 已知⊙O的半径为10,弦AB∥CD,AB=12,CD=16,则AB和CD的距离为 .2.如图,已知AB、AC为弦,OM⊥AB于点M, ON⊥AC于点N ,BC=4,求MN的长.2或14提高练习:3:在圆O中,直径CE⊥AB于
D,OD=4 ㎝,弦AC= ㎝ ,
求圆O的半径。
ABCDEO课堂小结:
请你谈谈:垂径定理可以解决一些怎样的问题?
课后作业:
基础训练:P33
(或CD过圆心)AE=BETCD⊥ABCD⊥ABAE=BETCD是直径
(或CD过圆心)推论三.一般地:在这五个结论中,如果有其中两个成立,就可以推出另外三个存在.
即:有2就有3例1. 已知:以O为圆心的两个同心圆,大圆的弦AB交小圆于C、D两点,求证:AC=BD .应用知识:变式. 已知:如图,线段AB与⊙O交于C、D两点,且OA=OB .求证:AC=BD ..证明圆中与弦有关的线段相等时, 常借助垂径定理,利用其平分弦的性质来解决问题. 例2.如图是一条排水管的截面。已知排水管的半径10cm,水面宽AB=12cm。求水的最大深度. ED求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. BAO练习1:如图,CD为圆O的直径,弦
AB交CD于E, ∠ CEB=30°,
DE=9㎝,CE=3㎝,求弦AB的长。O作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点.CDABE依据:变式一: 求弧AB的四等分点.CDABEFGmn弧AB的四等分点的典型错误.CDABMFG错在哪里?1.作AB的垂直平分线CD2.作AT、BT的垂直平分线EF、GHTENHP强调:等分弧时一定要作弧所对的弦的垂直平分线.变式二:你能确定弧AB的圆心吗?OABC ab方法:只要在圆弧上任意取两条弦,画这两条弦的垂直平分线,交点即为圆弧的圆心.变式三.你能找到原来车轮的圆心吗?1. 已知⊙O的半径为10,弦AB∥CD,AB=12,CD=16,则AB和CD的距离为 .2.如图,已知AB、AC为弦,OM⊥AB于点M, ON⊥AC于点N ,BC=4,求MN的长.2或14提高练习:3:在圆O中,直径CE⊥AB于
D,OD=4 ㎝,弦AC= ㎝ ,
求圆O的半径。
ABCDEO课堂小结:
请你谈谈:垂径定理可以解决一些怎样的问题?
课后作业:
基础训练:P33
同课章节目录
