3.3.2从函数观点看一元二次不等式 讲义(含解析)
文档属性
| 名称 | 3.3.2从函数观点看一元二次不等式 讲义(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 247.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 09:31:41 | ||
图片预览




文档简介
编号:016 课题:§3.3.2 从函数观点看一元二次不等式
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、经历从实际情境中抽象出一元二次不等式的过程,了解其意义.
2、会解一元二次不等式.
3、借助二次函数图象,了解一元二次不等式与相应函数、方程的联系.
本节重点难点
重点:一元二次不等式的解法;
难点:一元二次不等式与相应函数、方程的联系.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
1. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的____________叫作一元二次不等式.
【思考】
不等式是一元二次不等式吗
2、一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集 _______________ _______________
二次函数的解集 ______________ ______________ _____________
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【思考】
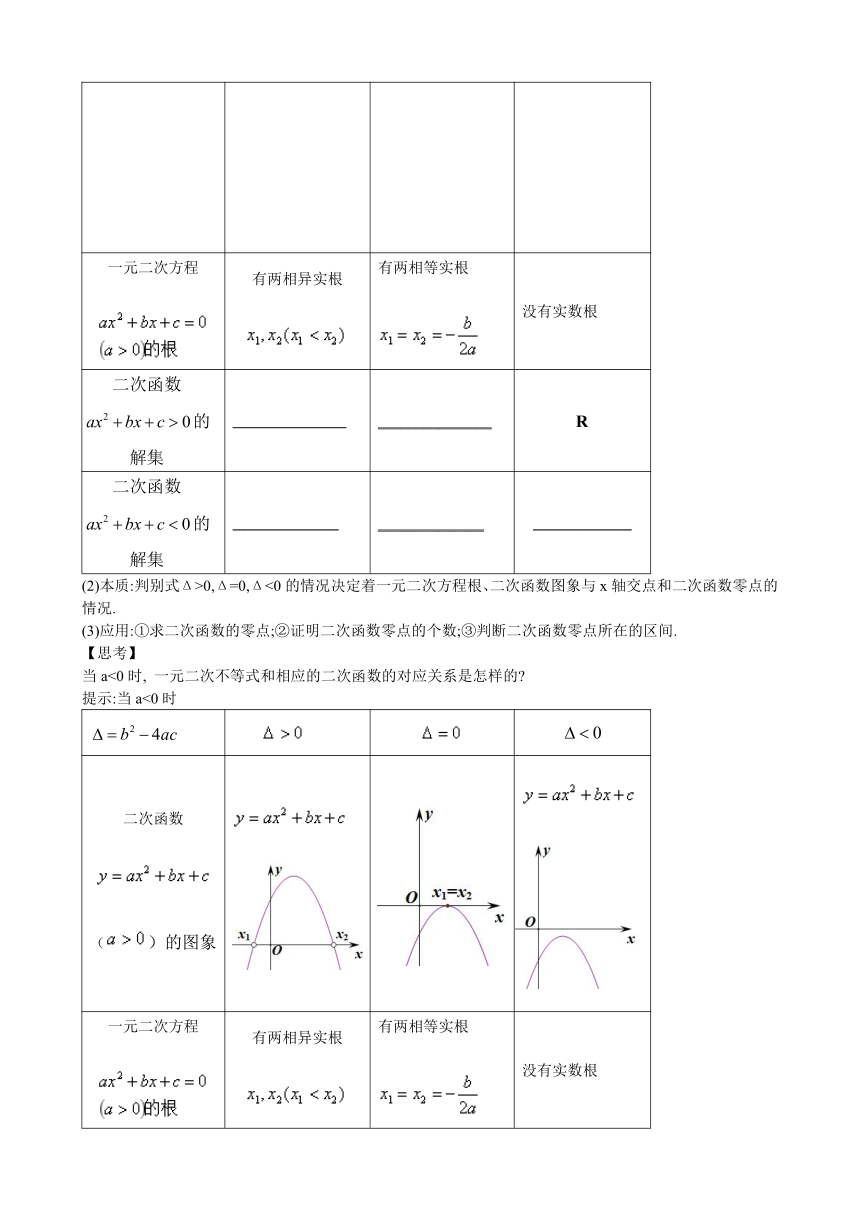
当a<0时, 一元二次不等式和相应的二次函数的对应关系是怎样的
提示:当a<0时
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集 _________________ _______________ ______________
二次函数的解集 ________________ ________________ ______________
(2)本质:方程和不等式或是函数的特殊情况,它们之间是一种包含关系,也就是当y=0时,函数就转化为方程,当或时就转化为一元二次不等式.
(3)应用:①解一元二次不等式,②已知一元二次不等式的解集求参数,③一元二次不等式的应用问题.
【思考】
(1)当时表中的可以有三重身份,你能说出是哪三重身份吗
(2)若一元二次不等式的解集为R,则实数应满足什么条件
【课前小题演练】
题1.已知集合M={x|-4A.{x|-4C.{x|-2题2.函数y=的自变量的取值范围是( )
A.{x|x<-4或x>3}
B.{x|-4<x<3}
C.{x|x≤-4或x≥3}
D.{x|-4≤x≤3}
题3.不等式>2的解集是( )
A. B.
C. D.
题4.若不等式ax2-x-c>0的解集为{x|-1题5.若2x2-5x+2<0,则+2|x-2|=( )
A.1 B.2 C.3 D.4
题6.若产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x2(0<x<240),若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是( )
A.100台 B.120台
C.150台 D.180台
题7(多选题).已知关于x的不等式ax2+bx-3<0,关于此不等式的解集有下列结论,其中正确的是( )
A.不等式ax2+bx-3<0的解集可以是R
B.不等式ax2+bx-3<0的解集可以是
C.不等式ax2+bx-3<0的解集可以是
D.不等式ax2+bx-3<0的解集可以是
题8(多选题).下列结论错误的是( )
A.若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R
B.不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0
C.若关于x的不等式ax2+x-1≤0的解集为R,则a≤-
D.不等式>1的解为x<1
题9.若二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点为(-1,0)和(3,0),则不等式ax2+bx+c<0的解集是________.
题10.若关于x的不等式ax-b<0的解集是,则关于x的不等式>0的解集是________.
题11.解不等式:0≤x2-x-2≤4.
【课堂题组训练】
题12. 在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.(0,2)
B.(-2,1)
C.(-∞,-2)∪(1,+∞)
D.(-1,2)
题13.若不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
A.[-1,4]
B.(-∞,-2]∪[5,+∞)
C.(-∞,-1]∪[4,+∞)
D.[-2,5]
题14(多选题).解关于x的不等式:ax2+(2-4a)x-8>0,则下列说法中正确的是( )
A.当a=0时,不等式的解集为
B.当a>0时,不等式的解集为x>4或
C.当a<0时,不等式的解集为
D.当a=-时,不等式的解集为
题15(多选题).若对任意x∈[a,a+2],不等式x2-2x-3≤0恒成立,则实数a的值可能为( )
A.-2 B.-1 C. D.2
题16(多选题).下面所给关于x的不等式,其中一定为一元二次不等式的是 ( )
A.3x+4<0 B.x2+mx-1>0 C.ax2+4x-7>0 D.x2<0
题17.某地每年销售木材约20万立方米,每立方米价格为2 400元.为了减少木材消耗,决定按销售收入的t%征收木材税,这样每年的木材销售量减少t万立方米.为了既减少木材消耗又保证税金收入每年不少于900万元,则t的取值范围是________.
题18.已知关于x的不等式ax+b>0的解集是(1,+∞),则=________,关于x的不等式>0的解集是________.
题19.已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.
(1)求a,b的值;
(2)解不等式ax2-(ac+b)x+bc<0.
题20.已知关于x的不等式x2-2mx+m+2≤0(m∈R)的解集为M.
(1)当M为空集时,求m的取值范围;
(2)在(1)的条件下,求的最小值;
(3)当M不为空集,且M 时,求实数m的取值范围.
【综合突破拔高】
题21.已知集合A=,B=,则A∩B=( )
A. B.
C. D.
题22.设m+n>0,则关于x的不等式(m-x)·(n+x)>0的解集是( )
A.{x|x<-n或x>m} B.{x|x-n}
C.{x|-n题23.不等式≥1的解集是( )
A. B.
C. D.
题24.已知函数y=ax2+2bx-c(a>0)的图象与x轴交于A,B两点,则不等式cx2+2bx-a<0的解集为( )
A.(-6,-2)
B.∪
C.
D.∪
题25.已知p:>,q: x∈R,ax2+ax+1>0,则p成立是q成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
题26.已知不等式-2x2+bx+c>0的解集是,若对于任意x∈,不等式-2x2+bx+c+t≤4恒成立,则t的取值范围是( )
A. B.
C. D.
题27(多选题).已知二次函数y=ax2+bx+c,且不等式y>-2x的解集为{x|1<x<3},则( )
A.a<0
B.方程ax2+bx+c=0的两个根是1,3
C.b=-4a-2
D.若方程y+6a=0有两个相等的根,则实数a=-
题28(多选题).关于x的不等式56x2+ax-a2<0的解集,以下叙述正确的是 ( )
A.当a>0时,不等式的解集为{x|-C.当a<0时,不等式的解集为{x|0时,不等式的解集为{x|题29(多选题).关于x的一元二次不等式x2-2x-a≤0的解集中有且仅有5个整数,则实数a的值可以是( )
A.2 B.4 C.6 D.8
题30(多选题).若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1则下列结论中正确的是 ( )
A.当m=0时,x1=2,x2=3 B.m>-
C.当m>0时,20时,x1<2<3题31.若关于x的不等式x2-3x+t<0的解集是{x|1<x<m},
则m=________,m+t=________.
题32.已知t是实数,若a,b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根,则的最小值是________.
题33.对任意实数x,不等式(a-3)x2-2(a-3)x-6<0恒成立,求实数a的取值范围.
题34.用可围成32 m墙的砖头,沿一面旧墙(旧墙足够长)围成四间猪舍(面积大小相等的长方形).应如何围才能使猪舍的总面积最大?最大面积是多少?
编号:016 课题:§3.3.2 从函数观点看一元二次不等式
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、经历从实际情境中抽象出一元二次不等式的过程,了解其意义.
2、会解一元二次不等式.
3、借助二次函数图象,了解一元二次不等式与相应函数、方程的联系.
本节重点难点
重点:一元二次不等式的解法;
难点:一元二次不等式与相应函数、方程的联系.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
1. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的_整式不等式_叫作一元二次不等式.
【思考】
不等式是一元二次不等式吗
提示:不是,一元二次不等式一定是整式不等式.
2、一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集
二次函数的解集
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【思考】
当a<0时, 一元二次不等式和相应的二次函数的对应关系是怎样的
提示:当a<0时
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集
二次函数的解集
(2)本质:方程和不等式或是函数的特殊情况,它们之间是一种包含关系,也就是当y=0时,函数就转化为方程,当或时就转化为一元二次不等式.
(3)应用:①解一元二次不等式,②已知一元二次不等式的解集求参数,③一元二次不等式的应用问题.
【思考】
(1)当时表中的可以有三重身份,你能说出是哪三重身份吗
提示: 既是二次函数图象与轴交点的横坐标(即二次函数的零点),又是一元
二次方程的两个解,还是一元二次不等式解集的区间端点.
(2)若一元二次不等式的解集为R,则实数应满足什么条件
提示:结合二次函数图象可知,若一元二次不等式的解集为,则,解得,所以不存在使不等式的解集为.
【课前小题演练】
题1.已知集合M={x|-4A.{x|-4C.{x|-2【解析】选C.由题意得,M={x|-4题2.函数y=的自变量的取值范围是( )
A.{x|x<-4或x>3}
B.{x|-4<x<3}
C.{x|x≤-4或x≥3}
D.{x|-4≤x≤3}
【解析】选C.由题意得函数满足x2+x-12≥0,
即(x-3)(x+4)≥0,解得x≤-4或x≥3,
所以函数的定义域为{x|x≤-4或x≥3}.
题3.不等式>2的解集是( )
A. B.
C. D.
【解析】选A.不等式>2,转化为-2>0,
即=>0,亦即(x-3)(3x-4)<0,解得<x<3,
故不等式的解集是.
题4.若不等式ax2-x-c>0的解集为{x|-1【解析】选C.由题可得-1和是方程ax2-x-c=0的两个根,且a<0,
所以解得a=-2,c=-1,则y=cx2-x-a=-x2-x+2=-,则函数图象开口向下,与x轴交于(-2,0),(1,0).
题5.若2x2-5x+2<0,则+2|x-2|=( )
A.1 B.2 C.3 D.4
【解析】选C.将不等式2x2-5x+2<0因式分解得(x-2)(2x-1)<0,
即或无解或所以+2|x-2|=+2|x-2|=2x-1+4-2x=3.
题6.若产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x2(0<x<240),若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是( )
A.100台 B.120台
C.150台 D.180台
【解析】选C.y-25x=-0.1x2-5x+3 000≤0,即x2+50x-30 000≥0,
解得x≥150或x≤-200(舍去).
故生产者不亏本的最低产量是150台.
题7(多选题).已知关于x的不等式ax2+bx-3<0,关于此不等式的解集有下列结论,其中正确的是( )
A.不等式ax2+bx-3<0的解集可以是R
B.不等式ax2+bx-3<0的解集可以是
C.不等式ax2+bx-3<0的解集可以是
D.不等式ax2+bx-3<0的解集可以是
【解析】选ABD.A:当a<0且Δ=b2+12a<0时,解集是R,正确;
B:当a=0,b=-1时,有-x-3<0,则解集是,正确;
C:当a≤0:解集不可能为空集;当a>0:Δ=b2+12a>0,解集不可能为空集,错误;D:当a=1,b=-2时,有(x-3)(x+1)<0,则解集是,正确.
题8(多选题).下列结论错误的是( )
A.若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R
B.不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0
C.若关于x的不等式ax2+x-1≤0的解集为R,则a≤-
D.不等式>1的解为x<1
【解析】选ABD.
A选项中,只有a>0时才成立;B选项当a=b=0,c≤0时也成立;D选项应为0<x<1.
题9.若二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点为(-1,0)和(3,0),则不等式ax2+bx+c<0的解集是________.
【解析】根据二次函数的图象知所求不等式的解集为(-∞,-1)∪(3,+∞).
答案:(-∞,-1)∪(3,+∞)
题10.若关于x的不等式ax-b<0的解集是,则关于x的不等式>0的解集是________.
【解析】因为ax-b<0的解集是,所以a=b且a<0,由>0得:==a>0,
所以<0,解得-50的解集为.
答案:
题11.解不等式:0≤x2-x-2≤4.
【解析】原不等式等价于
解x2-x-2≥0,得x≤-1或x≥2;
解x2-x-2≤4,得-2≤x≤3.
所以原不等式的解集为{x|x≤-1或x≥2}∩
{x|-2≤x≤3}={x|-2≤x≤-1或2≤x≤3}.
【课堂题组训练】
题12. 在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.(0,2)
B.(-2,1)
C.(-∞,-2)∪(1,+∞)
D.(-1,2)
【解题指南】先利用⊙运算的法则变形,再解不等式.
【解析】选B.由a⊙b=ab+2a+b,得x⊙(x-2)=
x(x-2)+2x+x-2=x2+x-2<0,所以-2<x<1.
题13.若不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
A.[-1,4]
B.(-∞,-2]∪[5,+∞)
C.(-∞,-1]∪[4,+∞)
D.[-2,5]
【解析】选A.x2-2x+5=(x-1)2+4的最小值为4,所以x2-2x+5≥a2-3a对任意实数x恒成立,只需a2-3a≤4,解得-1≤a≤4.
题14(多选题).解关于x的不等式:ax2+(2-4a)x-8>0,则下列说法中正确的是( )
A.当a=0时,不等式的解集为
B.当a>0时,不等式的解集为x>4或
C.当a<0时,不等式的解集为
D.当a=-时,不等式的解集为
【解析】选ABD.对于关于x的不等式:ax2+(2-4a)x-8>0,
(1)当a=0时,原不等式可化为:2x-8>0,解得x>4,即不等式的解集为;
(2)当a>0时,原不等式可化为:
>0,解得x>4或x<-,即不等式的解集为x>4或;
(3)当->0,解得4(4)当a=-时,原不等式可化为:2<0,无解,所以不等式的解集为 ;
(5)当a<-时,原不等式可化为:
>0,解得-题15(多选题).若对任意x∈[a,a+2],不等式x2-2x-3≤0恒成立,则实数a的值可能为( )
A.-2 B.-1 C. D.2
【解析】选BC.易得不等式x2-2x-3≤0的解集是[-1,3].
因为对任意x∈[a,a+2],不等式x2-2x-3≤0恒成立,所以[a,a+2] [-1,3],
所以解得-1≤a≤1.所以实数a的值可能为-1,.
题16(多选题).下面所给关于x的不等式,其中一定为一元二次不等式的是 ( )
A.3x+4<0 B.x2+mx-1>0 C.ax2+4x-7>0 D.x2<0
【解析】选BD.根据一元二次不等式的定义以及特征可判定A一定不是,C不一定是,B,D一定是.
题17.某地每年销售木材约20万立方米,每立方米价格为2 400元.为了减少木材消耗,决定按销售收入的t%征收木材税,这样每年的木材销售量减少t万立方米.为了既减少木材消耗又保证税金收入每年不少于900万元,则t的取值范围是________.
【解析】设按销售收入的t%征收木材税时,税金收入为y万元,则y=2 400×t%=60(8t-t2).
令y≥900,即60(8t-t2)≥900,解得3≤t≤5.
答案:[3,5]
题18.已知关于x的不等式ax+b>0的解集是(1,+∞),则=________,关于x的不等式>0的解集是________.
【解析】依题意,a>0且-=1,所以=-1;
不等式>0可变形为(ax-b)(x-2)>0,即(x-2)>0,所以(x+1)(x-2)>0,故x>2或x<-1.
答案:-1 {x|x<-1或x>2}
题19.已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.
(1)求a,b的值;
(2)解不等式ax2-(ac+b)x+bc<0.
【解析】(1) 因为不等式ax2-3x+6>4的解集为{x|x<1或x>b},所以x1=1与x2=b是方程ax2-3x+2=0的两个实数根,b>1且a>0.
由根与系数的关系,得解得
(2)由(1)知不等式ax2-(ac+b)x+bc<0可化为x2-(2+c)x+2c<0,即(x-2)(x-c)<0.
当c>2时,不等式(x-2)(x-c)<0的解集为{x|2<x<c};当c<2时,不等式(x-2)(x-c)<0的解集为{x|c<x<2};当c=2时,不等式(x-2)(x-c)<0的解集为 .
题20.已知关于x的不等式x2-2mx+m+2≤0(m∈R)的解集为M.
(1)当M为空集时,求m的取值范围;
(2)在(1)的条件下,求的最小值;
(3)当M不为空集,且M 时,求实数m的取值范围.
【解析】(1)因为M为空集,所以Δ=4m2-4(m+2)<0 m2-m-2<0 -1所以m的取值范围为;
(2)由(1)可知-12=4,当且仅当m+1= m=1时等号成立,所以的最小值为4;
(3)设函数y=x2-2mx+m+2,当M不为空集时,由M ,
得 2≤m≤.
所以实数m的取值范围为{m}.
【综合突破拔高】
题21.已知集合A=,B=,则A∩B=( )
A. B.
C. D.
【解析】选D.因为A=,B= ,
所以A∩B= .
题22.设m+n>0,则关于x的不等式(m-x)·(n+x)>0的解集是( )
A.{x|x<-n或x>m} B.{x|x-n}
C.{x|-n【解析】选C.方程(m-x)(n+x)=0的两个根分别为m,-n,
因为m+n>0,所以m>-n,结合二次函数y=(m-x)·(n+x)的图象,得原不等式的解集是{x|-n题23.不等式≥1的解集是( )
A. B.
C. D.
【解析】选B.不等式≥1,移项得-1≥0,
即≤0,可化为解得≤x<2,则原不等式的解集为.
题24.已知函数y=ax2+2bx-c(a>0)的图象与x轴交于A,B两点,则不等式cx2+2bx-a<0的解集为( )
A.(-6,-2)
B.∪
C.
D.∪
【解析】选D.由条件可知ax2+2bx-c=0的两个根分别为x1=2或x2=6,
则2+6=-,2×6=-,得b=-4a,c=-12a,所以cx2+2bx-a<0 -12ax2-8ax-a<0,
整理为12x2+8x+1>0 >0,解得x>-或x<-,所以不等式的解集是∪.
题25.已知p:>,q: x∈R,ax2+ax+1>0,则p成立是q成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】选A.求解不等式>可得0对于命题q,当a=0时,命题明显成立;
当a≠0时,有
解得0故p成立是q成立的充分不必要条件.
题26.已知不等式-2x2+bx+c>0的解集是,若对于任意x∈,不等式-2x2+bx+c+t≤4恒成立,则t的取值范围是( )
A. B.
C. D.
【解析】选B.由题意得-1和3是关于x的方程-2x2+bx+c=0的两个实数根,则,解得,则-2x2+bx+c=-2x2+4x+6,由-2x2+bx+c+t≤4得t≤2x2-4x-2,当-1≤x≤0时,min=-2,故t≤-2.
题27(多选题).已知二次函数y=ax2+bx+c,且不等式y>-2x的解集为{x|1<x<3},则( )
A.a<0
B.方程ax2+bx+c=0的两个根是1,3
C.b=-4a-2
D.若方程y+6a=0有两个相等的根,则实数a=-
【解析】选ACD.由于不等式y>-2x的解集为(1,3),即关于x的二次不等式ax2+(b+2)x+c>0的解集为{x|1<x<3},则a<0.由题意可知,1,3为关于x的二次方程ax2+(b+2)x+c=0的两根,
由根与系数的关系得-=1+3=4,=1×3=3,所以b=-4a-2,c=3a,所以y=ax2-(4a+2)x+3a.
由题意知,关于x的方程y+6a=0有两个相等的根,
即关于x的二次方程ax2-(4a+2)x+9a=0有两个相等的根,
则Δ=[-(4a+2)]2-36a2=(10a+2)(2-2a)=0,
因为a<0,解得a=-.
题28(多选题).关于x的不等式56x2+ax-a2<0的解集,以下叙述正确的是 ( )
A.当a>0时,不等式的解集为{x|-C.当a<0时,不等式的解集为{x|0时,不等式的解集为{x|【解析】选ABC.关于x的不等式56x2+ax-a2<0可化为(8x-a)(7x+a)<0,当a>0时,不等式的解集为;当a=0时,不等式的解集为 ;当a<0时,不等式的解集为.
题29(多选题).关于x的一元二次不等式x2-2x-a≤0的解集中有且仅有5个整数,则实数a的值可以是( )
A.2 B.4 C.6 D.8
【解析】选BC.设y=x2-2x-a,其图象为开口向上,对称轴是x=1的抛物线,如图所示.
若关于x的一元二次不等式x2-2x-a≤0的解集中有且仅有5个整数,
因为对称轴为x=1,则,即,
解得3≤a<8,所以a可以为4,6.
题30(多选题).若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1则下列结论中正确的是 ( )
A.当m=0时,x1=2,x2=3 B.m>-
C.当m>0时,20时,x1<2<3【解析】选ABD.A中,m=0时,方程为(x-2)(x-3)=0,解为:x1=2,x2=3,所以A正确;
B中,方程整理可得:x2-5x+6-m=0,由存在不相等的两个根的条件为:Δ=25-4(6-m)>0,可得m>-,所以B正确.当m>0时,即(x-2)(x-3)>0,函数f(x)=(x-2)(x-3)-m与x轴的交点(x1,0),(x2,0),如图可得x1<2<3题31.若关于x的不等式x2-3x+t<0的解集是{x|1<x<m},
则m=________,m+t=________.
【解析】因为不等式x2-3x+t<0的解集为{x|1<x<m},
所以1,m是方程x2-3x+t=0的两根,
所以,解得,所以t+m=4.
答案:2 4
题32.已知t是实数,若a,b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根,则的最小值是________.
【解析】因为a,b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根,所以可得a+b=2,ab=t-1≥0,所以t≥1,又Δ=4-4≥0,可得t≤2,所以1≤t≤2,
又=2-+1=2-2+2ab+1,
所以=2-4+2+1=t2-4,又因为1≤t≤2,所以-3≤t2-4≤0.
答案:-3
题33.对任意实数x,不等式(a-3)x2-2(a-3)x-6<0恒成立,求实数a的取值范围.
【解析】①当a-3=0,即a=3时,不等式为-6<0,恒成立,则a=3满足题意;
②当a-3≠0,即a≠3时,不等式恒成立则需:
,
解得-3题34.用可围成32 m墙的砖头,沿一面旧墙(旧墙足够长)围成四间猪舍(面积大小相等的长方形).应如何围才能使猪舍的总面积最大?最大面积是多少?
【解析】设长方形的一边(垂直于旧墙)长为x m,则另一边长为m,总面积S=x(32-5x)=-5x2+32x,0当x= m时,Smax= m2.
答:当长方形一边(垂直于旧墙)为 m,另一边为4 m时,猪舍面积最大,最大值为 m2.
- 0 -
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、经历从实际情境中抽象出一元二次不等式的过程,了解其意义.
2、会解一元二次不等式.
3、借助二次函数图象,了解一元二次不等式与相应函数、方程的联系.
本节重点难点
重点:一元二次不等式的解法;
难点:一元二次不等式与相应函数、方程的联系.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
1. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的____________叫作一元二次不等式.
【思考】
不等式是一元二次不等式吗
2、一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集 _______________ _______________
二次函数的解集 ______________ ______________ _____________
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【思考】
当a<0时, 一元二次不等式和相应的二次函数的对应关系是怎样的
提示:当a<0时
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集 _________________ _______________ ______________
二次函数的解集 ________________ ________________ ______________
(2)本质:方程和不等式或是函数的特殊情况,它们之间是一种包含关系,也就是当y=0时,函数就转化为方程,当或时就转化为一元二次不等式.
(3)应用:①解一元二次不等式,②已知一元二次不等式的解集求参数,③一元二次不等式的应用问题.
【思考】
(1)当时表中的可以有三重身份,你能说出是哪三重身份吗
(2)若一元二次不等式的解集为R,则实数应满足什么条件
【课前小题演练】
题1.已知集合M={x|-4
A.{x|x<-4或x>3}
B.{x|-4<x<3}
C.{x|x≤-4或x≥3}
D.{x|-4≤x≤3}
题3.不等式>2的解集是( )
A. B.
C. D.
题4.若不等式ax2-x-c>0的解集为{x|-1
A.1 B.2 C.3 D.4
题6.若产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x2(0<x<240),若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是( )
A.100台 B.120台
C.150台 D.180台
题7(多选题).已知关于x的不等式ax2+bx-3<0,关于此不等式的解集有下列结论,其中正确的是( )
A.不等式ax2+bx-3<0的解集可以是R
B.不等式ax2+bx-3<0的解集可以是
C.不等式ax2+bx-3<0的解集可以是
D.不等式ax2+bx-3<0的解集可以是
题8(多选题).下列结论错误的是( )
A.若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R
B.不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0
C.若关于x的不等式ax2+x-1≤0的解集为R,则a≤-
D.不等式>1的解为x<1
题9.若二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点为(-1,0)和(3,0),则不等式ax2+bx+c<0的解集是________.
题10.若关于x的不等式ax-b<0的解集是,则关于x的不等式>0的解集是________.
题11.解不等式:0≤x2-x-2≤4.
【课堂题组训练】
题12. 在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.(0,2)
B.(-2,1)
C.(-∞,-2)∪(1,+∞)
D.(-1,2)
题13.若不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
A.[-1,4]
B.(-∞,-2]∪[5,+∞)
C.(-∞,-1]∪[4,+∞)
D.[-2,5]
题14(多选题).解关于x的不等式:ax2+(2-4a)x-8>0,则下列说法中正确的是( )
A.当a=0时,不等式的解集为
B.当a>0时,不等式的解集为x>4或
C.当a<0时,不等式的解集为
D.当a=-时,不等式的解集为
题15(多选题).若对任意x∈[a,a+2],不等式x2-2x-3≤0恒成立,则实数a的值可能为( )
A.-2 B.-1 C. D.2
题16(多选题).下面所给关于x的不等式,其中一定为一元二次不等式的是 ( )
A.3x+4<0 B.x2+mx-1>0 C.ax2+4x-7>0 D.x2<0
题17.某地每年销售木材约20万立方米,每立方米价格为2 400元.为了减少木材消耗,决定按销售收入的t%征收木材税,这样每年的木材销售量减少t万立方米.为了既减少木材消耗又保证税金收入每年不少于900万元,则t的取值范围是________.
题18.已知关于x的不等式ax+b>0的解集是(1,+∞),则=________,关于x的不等式>0的解集是________.
题19.已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.
(1)求a,b的值;
(2)解不等式ax2-(ac+b)x+bc<0.
题20.已知关于x的不等式x2-2mx+m+2≤0(m∈R)的解集为M.
(1)当M为空集时,求m的取值范围;
(2)在(1)的条件下,求的最小值;
(3)当M不为空集,且M 时,求实数m的取值范围.
【综合突破拔高】
题21.已知集合A=,B=,则A∩B=( )
A. B.
C. D.
题22.设m+n>0,则关于x的不等式(m-x)·(n+x)>0的解集是( )
A.{x|x<-n或x>m} B.{x|x
C.{x|-n
A. B.
C. D.
题24.已知函数y=ax2+2bx-c(a>0)的图象与x轴交于A,B两点,则不等式cx2+2bx-a<0的解集为( )
A.(-6,-2)
B.∪
C.
D.∪
题25.已知p:>,q: x∈R,ax2+ax+1>0,则p成立是q成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
题26.已知不等式-2x2+bx+c>0的解集是,若对于任意x∈,不等式-2x2+bx+c+t≤4恒成立,则t的取值范围是( )
A. B.
C. D.
题27(多选题).已知二次函数y=ax2+bx+c,且不等式y>-2x的解集为{x|1<x<3},则( )
A.a<0
B.方程ax2+bx+c=0的两个根是1,3
C.b=-4a-2
D.若方程y+6a=0有两个相等的根,则实数a=-
题28(多选题).关于x的不等式56x2+ax-a2<0的解集,以下叙述正确的是 ( )
A.当a>0时,不等式的解集为{x|-
A.2 B.4 C.6 D.8
题30(多选题).若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1
A.当m=0时,x1=2,x2=3 B.m>-
C.当m>0时,2
则m=________,m+t=________.
题32.已知t是实数,若a,b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根,则的最小值是________.
题33.对任意实数x,不等式(a-3)x2-2(a-3)x-6<0恒成立,求实数a的取值范围.
题34.用可围成32 m墙的砖头,沿一面旧墙(旧墙足够长)围成四间猪舍(面积大小相等的长方形).应如何围才能使猪舍的总面积最大?最大面积是多少?
编号:016 课题:§3.3.2 从函数观点看一元二次不等式
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、经历从实际情境中抽象出一元二次不等式的过程,了解其意义.
2、会解一元二次不等式.
3、借助二次函数图象,了解一元二次不等式与相应函数、方程的联系.
本节重点难点
重点:一元二次不等式的解法;
难点:一元二次不等式与相应函数、方程的联系.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
1. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的_整式不等式_叫作一元二次不等式.
【思考】
不等式是一元二次不等式吗
提示:不是,一元二次不等式一定是整式不等式.
2、一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集
二次函数的解集
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【思考】
当a<0时, 一元二次不等式和相应的二次函数的对应关系是怎样的
提示:当a<0时
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集
二次函数的解集
(2)本质:方程和不等式或是函数的特殊情况,它们之间是一种包含关系,也就是当y=0时,函数就转化为方程,当或时就转化为一元二次不等式.
(3)应用:①解一元二次不等式,②已知一元二次不等式的解集求参数,③一元二次不等式的应用问题.
【思考】
(1)当时表中的可以有三重身份,你能说出是哪三重身份吗
提示: 既是二次函数图象与轴交点的横坐标(即二次函数的零点),又是一元
二次方程的两个解,还是一元二次不等式解集的区间端点.
(2)若一元二次不等式的解集为R,则实数应满足什么条件
提示:结合二次函数图象可知,若一元二次不等式的解集为,则,解得,所以不存在使不等式的解集为.
【课前小题演练】
题1.已知集合M={x|-4
A.{x|x<-4或x>3}
B.{x|-4<x<3}
C.{x|x≤-4或x≥3}
D.{x|-4≤x≤3}
【解析】选C.由题意得函数满足x2+x-12≥0,
即(x-3)(x+4)≥0,解得x≤-4或x≥3,
所以函数的定义域为{x|x≤-4或x≥3}.
题3.不等式>2的解集是( )
A. B.
C. D.
【解析】选A.不等式>2,转化为-2>0,
即=>0,亦即(x-3)(3x-4)<0,解得<x<3,
故不等式的解集是.
题4.若不等式ax2-x-c>0的解集为{x|-1
所以解得a=-2,c=-1,则y=cx2-x-a=-x2-x+2=-,则函数图象开口向下,与x轴交于(-2,0),(1,0).
题5.若2x2-5x+2<0,则+2|x-2|=( )
A.1 B.2 C.3 D.4
【解析】选C.将不等式2x2-5x+2<0因式分解得(x-2)(2x-1)<0,
即或无解或
题6.若产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3 000+20x-0.1x2(0<x<240),若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是( )
A.100台 B.120台
C.150台 D.180台
【解析】选C.y-25x=-0.1x2-5x+3 000≤0,即x2+50x-30 000≥0,
解得x≥150或x≤-200(舍去).
故生产者不亏本的最低产量是150台.
题7(多选题).已知关于x的不等式ax2+bx-3<0,关于此不等式的解集有下列结论,其中正确的是( )
A.不等式ax2+bx-3<0的解集可以是R
B.不等式ax2+bx-3<0的解集可以是
C.不等式ax2+bx-3<0的解集可以是
D.不等式ax2+bx-3<0的解集可以是
【解析】选ABD.A:当a<0且Δ=b2+12a<0时,解集是R,正确;
B:当a=0,b=-1时,有-x-3<0,则解集是,正确;
C:当a≤0:解集不可能为空集;当a>0:Δ=b2+12a>0,解集不可能为空集,错误;D:当a=1,b=-2时,有(x-3)(x+1)<0,则解集是,正确.
题8(多选题).下列结论错误的是( )
A.若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R
B.不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0
C.若关于x的不等式ax2+x-1≤0的解集为R,则a≤-
D.不等式>1的解为x<1
【解析】选ABD.
A选项中,只有a>0时才成立;B选项当a=b=0,c≤0时也成立;D选项应为0<x<1.
题9.若二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点为(-1,0)和(3,0),则不等式ax2+bx+c<0的解集是________.
【解析】根据二次函数的图象知所求不等式的解集为(-∞,-1)∪(3,+∞).
答案:(-∞,-1)∪(3,+∞)
题10.若关于x的不等式ax-b<0的解集是,则关于x的不等式>0的解集是________.
【解析】因为ax-b<0的解集是,所以a=b且a<0,由>0得:==a>0,
所以<0,解得-5
答案:
题11.解不等式:0≤x2-x-2≤4.
【解析】原不等式等价于
解x2-x-2≥0,得x≤-1或x≥2;
解x2-x-2≤4,得-2≤x≤3.
所以原不等式的解集为{x|x≤-1或x≥2}∩
{x|-2≤x≤3}={x|-2≤x≤-1或2≤x≤3}.
【课堂题组训练】
题12. 在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.(0,2)
B.(-2,1)
C.(-∞,-2)∪(1,+∞)
D.(-1,2)
【解题指南】先利用⊙运算的法则变形,再解不等式.
【解析】选B.由a⊙b=ab+2a+b,得x⊙(x-2)=
x(x-2)+2x+x-2=x2+x-2<0,所以-2<x<1.
题13.若不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
A.[-1,4]
B.(-∞,-2]∪[5,+∞)
C.(-∞,-1]∪[4,+∞)
D.[-2,5]
【解析】选A.x2-2x+5=(x-1)2+4的最小值为4,所以x2-2x+5≥a2-3a对任意实数x恒成立,只需a2-3a≤4,解得-1≤a≤4.
题14(多选题).解关于x的不等式:ax2+(2-4a)x-8>0,则下列说法中正确的是( )
A.当a=0时,不等式的解集为
B.当a>0时,不等式的解集为x>4或
C.当a<0时,不等式的解集为
D.当a=-时,不等式的解集为
【解析】选ABD.对于关于x的不等式:ax2+(2-4a)x-8>0,
(1)当a=0时,原不等式可化为:2x-8>0,解得x>4,即不等式的解集为;
(2)当a>0时,原不等式可化为:
>0,解得x>4或x<-,即不等式的解集为x>4或;
(3)当-
(5)当a<-时,原不等式可化为:
>0,解得-
A.-2 B.-1 C. D.2
【解析】选BC.易得不等式x2-2x-3≤0的解集是[-1,3].
因为对任意x∈[a,a+2],不等式x2-2x-3≤0恒成立,所以[a,a+2] [-1,3],
所以解得-1≤a≤1.所以实数a的值可能为-1,.
题16(多选题).下面所给关于x的不等式,其中一定为一元二次不等式的是 ( )
A.3x+4<0 B.x2+mx-1>0 C.ax2+4x-7>0 D.x2<0
【解析】选BD.根据一元二次不等式的定义以及特征可判定A一定不是,C不一定是,B,D一定是.
题17.某地每年销售木材约20万立方米,每立方米价格为2 400元.为了减少木材消耗,决定按销售收入的t%征收木材税,这样每年的木材销售量减少t万立方米.为了既减少木材消耗又保证税金收入每年不少于900万元,则t的取值范围是________.
【解析】设按销售收入的t%征收木材税时,税金收入为y万元,则y=2 400×t%=60(8t-t2).
令y≥900,即60(8t-t2)≥900,解得3≤t≤5.
答案:[3,5]
题18.已知关于x的不等式ax+b>0的解集是(1,+∞),则=________,关于x的不等式>0的解集是________.
【解析】依题意,a>0且-=1,所以=-1;
不等式>0可变形为(ax-b)(x-2)>0,即(x-2)>0,所以(x+1)(x-2)>0,故x>2或x<-1.
答案:-1 {x|x<-1或x>2}
题19.已知不等式ax2-3x+6>4的解集为{x|x<1或x>b}.
(1)求a,b的值;
(2)解不等式ax2-(ac+b)x+bc<0.
【解析】(1) 因为不等式ax2-3x+6>4的解集为{x|x<1或x>b},所以x1=1与x2=b是方程ax2-3x+2=0的两个实数根,b>1且a>0.
由根与系数的关系,得解得
(2)由(1)知不等式ax2-(ac+b)x+bc<0可化为x2-(2+c)x+2c<0,即(x-2)(x-c)<0.
当c>2时,不等式(x-2)(x-c)<0的解集为{x|2<x<c};当c<2时,不等式(x-2)(x-c)<0的解集为{x|c<x<2};当c=2时,不等式(x-2)(x-c)<0的解集为 .
题20.已知关于x的不等式x2-2mx+m+2≤0(m∈R)的解集为M.
(1)当M为空集时,求m的取值范围;
(2)在(1)的条件下,求的最小值;
(3)当M不为空集,且M 时,求实数m的取值范围.
【解析】(1)因为M为空集,所以Δ=4m2-4(m+2)<0 m2-m-2<0 -1
(2)由(1)可知-1
(3)设函数y=x2-2mx+m+2,当M不为空集时,由M ,
得 2≤m≤.
所以实数m的取值范围为{m}.
【综合突破拔高】
题21.已知集合A=,B=,则A∩B=( )
A. B.
C. D.
【解析】选D.因为A=,B= ,
所以A∩B= .
题22.设m+n>0,则关于x的不等式(m-x)·(n+x)>0的解集是( )
A.{x|x<-n或x>m} B.{x|x
C.{x|-n
因为m+n>0,所以m>-n,结合二次函数y=(m-x)·(n+x)的图象,得原不等式的解集是{x|-n
A. B.
C. D.
【解析】选B.不等式≥1,移项得-1≥0,
即≤0,可化为解得≤x<2,则原不等式的解集为.
题24.已知函数y=ax2+2bx-c(a>0)的图象与x轴交于A,B两点,则不等式cx2+2bx-a<0的解集为( )
A.(-6,-2)
B.∪
C.
D.∪
【解析】选D.由条件可知ax2+2bx-c=0的两个根分别为x1=2或x2=6,
则2+6=-,2×6=-,得b=-4a,c=-12a,所以cx2+2bx-a<0 -12ax2-8ax-a<0,
整理为12x2+8x+1>0 >0,解得x>-或x<-,所以不等式的解集是∪.
题25.已知p:>,q: x∈R,ax2+ax+1>0,则p成立是q成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】选A.求解不等式>可得0
当a≠0时,有
解得0
题26.已知不等式-2x2+bx+c>0的解集是,若对于任意x∈,不等式-2x2+bx+c+t≤4恒成立,则t的取值范围是( )
A. B.
C. D.
【解析】选B.由题意得-1和3是关于x的方程-2x2+bx+c=0的两个实数根,则,解得,则-2x2+bx+c=-2x2+4x+6,由-2x2+bx+c+t≤4得t≤2x2-4x-2,当-1≤x≤0时,min=-2,故t≤-2.
题27(多选题).已知二次函数y=ax2+bx+c,且不等式y>-2x的解集为{x|1<x<3},则( )
A.a<0
B.方程ax2+bx+c=0的两个根是1,3
C.b=-4a-2
D.若方程y+6a=0有两个相等的根,则实数a=-
【解析】选ACD.由于不等式y>-2x的解集为(1,3),即关于x的二次不等式ax2+(b+2)x+c>0的解集为{x|1<x<3},则a<0.由题意可知,1,3为关于x的二次方程ax2+(b+2)x+c=0的两根,
由根与系数的关系得-=1+3=4,=1×3=3,所以b=-4a-2,c=3a,所以y=ax2-(4a+2)x+3a.
由题意知,关于x的方程y+6a=0有两个相等的根,
即关于x的二次方程ax2-(4a+2)x+9a=0有两个相等的根,
则Δ=[-(4a+2)]2-36a2=(10a+2)(2-2a)=0,
因为a<0,解得a=-.
题28(多选题).关于x的不等式56x2+ax-a2<0的解集,以下叙述正确的是 ( )
A.当a>0时,不等式的解集为{x|-
题29(多选题).关于x的一元二次不等式x2-2x-a≤0的解集中有且仅有5个整数,则实数a的值可以是( )
A.2 B.4 C.6 D.8
【解析】选BC.设y=x2-2x-a,其图象为开口向上,对称轴是x=1的抛物线,如图所示.
若关于x的一元二次不等式x2-2x-a≤0的解集中有且仅有5个整数,
因为对称轴为x=1,则,即,
解得3≤a<8,所以a可以为4,6.
题30(多选题).若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1
A.当m=0时,x1=2,x2=3 B.m>-
C.当m>0时,2
B中,方程整理可得:x2-5x+6-m=0,由存在不相等的两个根的条件为:Δ=25-4(6-m)>0,可得m>-,所以B正确.当m>0时,即(x-2)(x-3)>0,函数f(x)=(x-2)(x-3)-m与x轴的交点(x1,0),(x2,0),如图可得x1<2<3
则m=________,m+t=________.
【解析】因为不等式x2-3x+t<0的解集为{x|1<x<m},
所以1,m是方程x2-3x+t=0的两根,
所以,解得,所以t+m=4.
答案:2 4
题32.已知t是实数,若a,b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根,则的最小值是________.
【解析】因为a,b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根,所以可得a+b=2,ab=t-1≥0,所以t≥1,又Δ=4-4≥0,可得t≤2,所以1≤t≤2,
又=2-+1=2-2+2ab+1,
所以=2-4+2+1=t2-4,又因为1≤t≤2,所以-3≤t2-4≤0.
答案:-3
题33.对任意实数x,不等式(a-3)x2-2(a-3)x-6<0恒成立,求实数a的取值范围.
【解析】①当a-3=0,即a=3时,不等式为-6<0,恒成立,则a=3满足题意;
②当a-3≠0,即a≠3时,不等式恒成立则需:
,
解得-3
【解析】设长方形的一边(垂直于旧墙)长为x m,则另一边长为m,总面积S=x(32-5x)=-5x2+32x,0
答:当长方形一边(垂直于旧墙)为 m,另一边为4 m时,猪舍面积最大,最大值为 m2.
- 0 -
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
