第七章平行线的证明 单元复习题(含解析) 2022--2023学年北师大版八年级数学上册
文档属性
| 名称 | 第七章平行线的证明 单元复习题(含解析) 2022--2023学年北师大版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 466.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 11:37:27 | ||
图片预览




文档简介
北师大版八年级数学上册第七章平行线的证明 单元复习题
一、选择题
1.如图,直线,一直角三角板ABC(∠ACB=90° )放在平行线上,两直角边分别l1与l2、交于点D、E,现测得∠1=75°,则∠2的度数为( )
A.15° B.25° C.30° D.35°
2.对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A.a=﹣3,b=2 B.a=3,b=2 C.a=3,b=﹣1 D.a=﹣1,b=3
3.如图,下列条件中,一定能判断的是( )
A. B. C. D.
4.下列命题中,是假命题的是( )
A.平面内,若ab,a⊥c,那么b⊥c
B.两直线平行,同位角相等
C.负数的平方根是负数
D.若,则a=b
5.已知在中,,,则的度数是( )
A. B. C. D.
6.如图,在平面直角坐标系中,,,,,…根据这个规律,点的坐标是( )
A. B. C. D.
7.能说明命题“一个钝角与一个锐角的差一定是锐角”是假命题的反例是( )
A. B.
C. D.
8.如图,给出下列条件.①;②;③,且;④其中,能推出的条作为( )
A.①②③ B.①②④ C.①③④ D.②③④
9.如图,,平分,D是的中点,,则( )
A. B. C. D.
10.已知等腰三角形一腰上的高与另一腰的夹角为,那么这个等腰三角形的顶角等于( )
A.或 B. C. D.或
二、填空题
11.如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着 的展开式 的系数;第五行的五个数恰好对应着 的展开式 的系数;根据数表中前五行的数字所反映的规律,则 .
12.将“同角的补角相等”改写成“如果……那么……”的形式为 .
13.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
14.等腰中,,平分,若,则 .
三、解答题
15.如图,已知,则,,之间的关系是: ▲ ,请写出你的证明过程.
16.判断下列命题的真假,若是假命题,请举出反例;若是真命题,请给出证明.
若 ,则 ;
三个角对应相等的两个三角形全等.
17.如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.
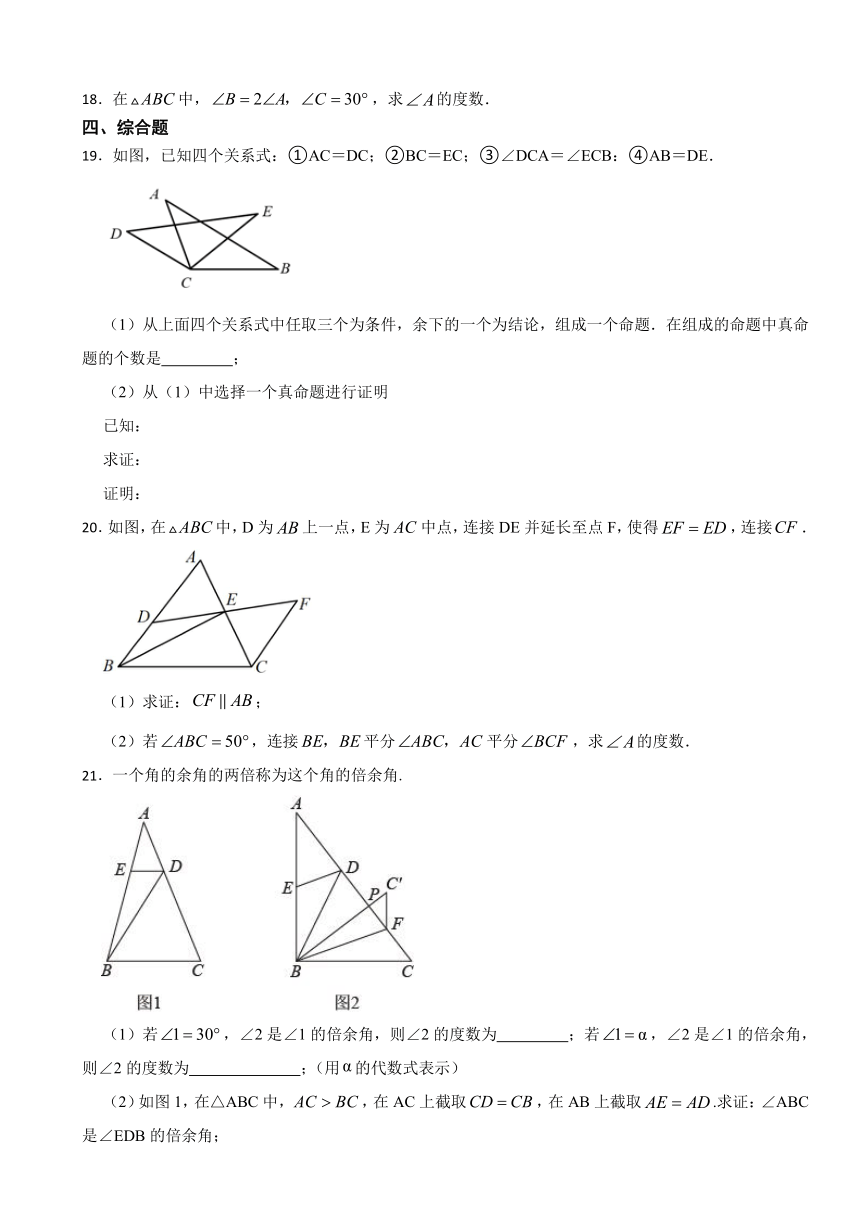
18.在中,,求的度数.
四、综合题
19.如图,已知四个关系式:①AC=DC;②BC=EC;③∠DCA=∠ECB:④AB=DE.
(1)从上面四个关系式中任取三个为条件,余下的一个为结论,组成一个命题.在组成的命题中真命题的个数是 ;
(2)从(1)中选择一个真命题进行证明
已知:
求证:
证明:
20.如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得,连接.
(1)求证:;
(2)若,连接平分平分,求的度数.
21.一个角的余角的两倍称为这个角的倍余角.
(1)若,∠2是∠1的倍余角,则∠2的度数为 ;若,∠2是∠1的倍余角,则∠2的度数为 ;(用的代数式表示)
(2)如图1,在△ABC中,,在AC上截取,在AB上截取.求证:∠ABC是∠EDB的倍余角;
(3)如图2,在(2)的情况下,作交AC于点F,将△BFC沿BF折叠得到,交AC于点P,若,设,求∠CPB的度数.
22.定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为,那么称此三角形为“倍角互余三角形”.
(1)【基础巩固】若是“倍角互余三角形”,,,则 ;
(2)【尝试应用】如图1,在中,,点为线段上一点,若与互余.求证:是“倍角互余三角形”;
(3)【拓展提高】如图2,在中,,,,试问在边上是否存在点,使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:如图,过点C作CF∥l1,
∵l1∥l2,
∴CF∥l1∥l2,
∴∠FCD=∠1=75°,∠BCF=∠2,
∵∠ACB=90°,
∴∠1+∠2=90°,
∴∠2=90°-75°=15°,
故答案为:A.
【分析】过点C作CF∥l1,根据平行公理得出CF∥l1∥l2,得出∠FCD=∠1=75°,∠BCF=∠2,再根据∠ACB=90°得出∠1+∠2=90°,即可得出∠2=90°-75°=15°.
2.【答案】A
【解析】【解答】解:A、a=-3,b=2,满足a2>b2,a<b,能说明命题是假命题;
B、a=3,b=2,满足a2>b2,a>b,不能说明命题是假命题;
C、a=3,b= 1,满足a2>b2,a>b,不能说明命题是假命题;
D、a= 1,b=3,不满足a2>b2,不能说明命题是假命题.
故答案为:A.
【分析】通过计算判定,满足a2>b2,不满足a>b即可.
3.【答案】B
【解析】【解答】解:A、∠2与∠3不是两条直线被第三条直线所截形成的角,所以即使相等也不能判断AB∥CD,故本选项错误;
B、∠1与∠2是AB、CD两条直线被第三条直线所截形成的内错角,根据内错角相等,两直线平行,可得AB∥CD,故本选项正确;
C、∠4与∠5不是两条直线被第三条直线所截形成的角,所以即使相等也不能判断AB∥CD,故本选项错误;
D、∠3与∠4是AB、CD两条直线被第三条直线所截形成的同旁内角,即使相等,也不能判断AB∥CD,故本选项错误.
故答案为:B.
【分析】两条直线被第三条直线所截形成同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此判断.
4.【答案】C
【解析】【解答】解:A、平面内,若a∥b,a⊥c,那么b⊥c,是真命题,不符合题意;
B、两直线平行,同位角相等,是真命题,不符合题意;
C、负数没有平方根,故本说法是假命题,符合题意;
D、若,则a=b,是真命题,不符合题意.
故答案为:C.
【分析】根据二直线平行,同位角相等及垂直的定义即可判断A;根据平行线的性质,可判断B;根据负数没有平方根可判断C;根据算术平方根的双重非负性可判断D.
5.【答案】B
【解析】【解答】解:在中,,,
,
故答案为:B.
【分析】直接根据内角和定理计算即可.
6.【答案】C
【解析】【解答】解:观察图形可知,横坐标依次为1、2、3、4、、n,纵坐标依次为-2、0、2、0、,四个一循环,
∵,
∴点的坐标是.
故答案为:C
【分析】先求出规律,再结合,即可得到点的坐标是。
7.【答案】D
【解析】【解答】解:A、是锐角,不符合题意;
B、与是两个锐角,不符合题意;
C、是锐角,不符合题意;
D、是钝角,符合题意.
故答案为:D.
【分析】原命题为假命题时,应满足一个钝角与一个锐角的差不是锐角,据此判断.
8.【答案】C
【解析】【解答】解:①∵,
∴,正确,符合题意;
②∵,
∴,(内错角相等,两直线平行),选项不符合题意;
③∵,,
∴,
∴,正确,符合题意;
④∵,
∴,由同位角相等,两直线平行可得,正确,符合题意;
故能推出的条件为①③④.
故答案为:C.
【分析】两条直线被第三条直线所截,如果同位角相等,那么被截的两直线平行;两条直线被第三条直线所截,如果内错角相等,那么被截的两直线平行;两条直线被第三条直线所截,如果同旁内角互补,那么被截的两直线平行;从而一一判断即可得出答案.
9.【答案】B
【解析】【解答】解:∵CB平分∠ACE,∠ACE=110°
∴∠BCE=∠BCA=55°
∵CE//AB
∴∠BCE=∠B=55°
∴∠BCA=∠B=55°
∴AC=AB
∵D为BC中点
∴AD⊥BC,即∠ADB=90°
∴∠DAB=180°-∠B-∠ADB=180°-55°-90°=35°
故答案为:B.
【分析】根据角平分线的性质和平行线的性质,可以得出∠BCA=∠B=55°,从而得到AB=AC,再由点D是BC中点,跟等腰三角形三线合一的性质可知∠ADB=90°,最后根据∠DAB=180°-∠B-∠ADB,即可求解.
10.【答案】A
【解析】【解答】解:
如图(1),当是锐角三角形时,
,,
,
,
;
如图(2),当是钝角三角形时,
,,
,
,
,;
综上所述,它的顶角度数为:或,
故答案为:A.
【分析】分两种情况:①当是锐角三角形时,②当是钝角三角形时,再分别画出图象并利用三角形的内角和及等腰三角形的性质求解即可。
11.【答案】a5+5a4b+10a3b2+10a2b3+5ab4+b5
【解析】【解答】由图形可得
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
∴答案为:a5+5a4b+10a3b2+10a2b3+5ab4+b5.
【分析】观察图表寻找规律:三角形是一个由数字排列成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
12.【答案】如果两个角是同一个角的补角,那么这两个角相等
【解析】【解答】解:将“同角的补角相等”改写成“如果……那么……”的形式为
如果两个角是同一个角的补角,那么这两个角相等.
故答案为:如果两个角是同一个角的补角,那么这两个角相等
【分析】要将一个命题写成“如果……那么……”的形式,就要分清命题的题设和结论,如果后面是题设,那么的后面是结论,即可求解.
13.【答案】20°
【解析】【解答】解:过点C作CF∥AE,
∵AE∥BD,
∴AE∥BD∥CF,
∴∠2=∠DCF=30°,∠EAC+∠ACF=180°,
∵∠1=∠EAC=130°,
∴∠ACF=∠ACE+∠DCF=180°-130°=50°,
∴∠ACE=50°-30°=20°.
故答案为:20°
【分析】过点C作CF∥AE,利用同平行与一条直线的两直线平行,可证得AE∥BD∥CF,利用平行线的性质可求出∠DCF的度数,同时可证得∠EAC+∠ACF=180°,由此可求出∠ACF的度数,即可求出∠ACE的度数.
14.【答案】100°
【解析】【解答】解:如图所示,
∵AB=AC,
∴∠C=∠ABC,
又∵BD平分∠ABC,
∴∠1=∠2=∠ABC,
∴∠C=2∠1,
∵∠2+∠C=180°-∠BDC,且∠BDC=120°,
∴3∠1=60°,即∠1=∠2=20°,
又∵∠BDC=∠A+∠1,
∴∠A=∠BDC-∠1=120°-20°=100°.
故答案为:100°.
【分析】由AB=AC,根据等边对等角,可得∠ABC=∠C,又由BD平分∠ABC,∠BDC=120°,可求得∠1的度数,然后根据三角形内角和定理,即可求得∠A的度数.
15.【答案】结论:∠APC=∠A+∠C.
证明:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A=∠APE,∠C=∠CPE,
∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C.
【解析】【分析】过点P作PE∥AB,利用在同一个平面内,同平行于一条直线的两直线平行,可证得PE∥AB∥CD,利用平行线的性质可推出∠A=∠APE,∠C=∠CPE;然后根据∠APC=∠APE+∠CPE,可得到∠A,∠C,∠APC之间的关系.
16.【答案】解: 若 ,则 是假命题,
例如: , ,
,但 ;
三个角对应相等的两个三角形全等是假命题,
例如:两个边长不相等的等边三角形不全等.
【解析】【分析】(1)可以用特殊值法:取 , 进行判断即可.(2)可以举反例说明, 例如:两个边长不相等的等边三角形不全等.
17.【答案】证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在和中,
,
∴,
∴,
∴AC∥DF.
【解析】【分析】根据BE=CF以及线段的和差关系可得BC=EF,由已知条件可知AB=DE,∠ABC=∠DEF,利用SAS证明△ABC≌△DEF,得到∠ACB=∠F,然后根据平行线的判定定理进行证明.
18.【答案】解:设,则,
∵,
∴,
解得,
∴.
【解析】【分析】设,则,利用三角形的内角和可得,再求出x的值即可。
19.【答案】(1)2
(2)解:若选①②③为条件,④为结论,
已知:AC=DC,BC=EC,∠DCA=∠ECB.
求证:AB=DE.
证明:∵∠DCA=∠ECB,
∴∠DCA+∠ACE=∠BCE+∠ACE,即∠ACB=∠DCE,
在△ACB和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE.
【解析】【解答】解:(1)若①②③为条件,④为结论,
则可利用SAS证明△ACB≌△DCE,可得④;
若①②④为条件,③为结论,
则可利用SSS证明△ACB≌△DCE,可得③;
若①③④为条件,②为结论,
无法证明△ACB≌△DCE,则不可得②;
若②③④为条件,①为结论,
无法证明△ACB≌△DCE,则不可得①;
∴真命题的个数是2;
【分析】(1)根据真命题的定义求解即可;
(2)结合(1)的条件,利用“SAS”证明△ACB≌△DCE,即可得到AB=DE。
20.【答案】(1)证明:∵E为中点,
∴,
在和中,
,
∴,
∴,
∴;
(2)解:由(1)得:,
∵平分,
∴,
∴,
∵,
∴
【解析】【分析】(1)根据SAS证明△ADE≌△CFE,可得∠A=∠ECF,根据平行线的判定即证;
(2)由(1)知∠A=∠ECF,由角平分线的定义可得,利用等量代换即可求解.
21.【答案】(1)120°;
(2)解:设,
∵CD=CB,AE=AD
∴,
∴,
,
∴即∠ABC是∠EDB的倍余角.
(3)解:由(2)得,
∵,
∴,
∵,
∴,
∴,
∴,.
【解析】【解答】解:(1)∵∠1=30°,∠2是∠1的倍余角,
∴∠2=2(90° 30°)=120°;
∵∠1=α,∠2是∠1的倍余角,
∴∠2=2(90° α)=180° 2α.
故答案为:120°;180° 2α.
【分析】(1)根据∠2是∠1的倍余角可得∠2=2×(90°-∠1),据此解答;
(2)设∠AED=a,∠CBD=b,由等腰三角形的性质可得∠AED=∠ADE=a,∠DBC=∠BDC=b,由内角和定理可得∠EDB=180°-a-b,∠ABC=180°-(180°-2a)-(180°-2b)=2a+2b+180°,甲车证明;
(3)由(2)得∠EDB=45°,根据平行线的性质可得∠EDB=∠DBF=45°,根据等腰三角形的性质可得∠DBC=45°+a=∠BDC,则∠DBP=45°-a,∠DBP+∠DBC=90°,甲车解答.
22.【答案】(1)15
(2)证明:∵,
∴,
又∵,
∴,
∴
∴是倍角互余三角形.
(3)解:①当平分时,则,
∴,
∴,则,
设,则,,
在中,,
解得,所以.
②当时,作点关于的对称点,连接、,并延长交于点.
设,则,
∵点、点关于对称,
∴,
∴,
∴,
即,
利用等积法求得:,
∴,
在中,
设,在中,,
∴,
在中,,
∴,
综上所述,或时,为倍角互余三角形.
【解析】【解答】解:(1)∵是“倍角互余三角形”,,,
∴,
∴,
故答案为:15;
【分析】(1)由题意可得∠A+2∠B=90°,据此计算;
(2)由内角和定理可得∠B+∠CAB=90°,由题意可得∠CAB+∠CAD=90°,则∠B=∠CAD,∠B+∠CAD+∠BAD=2∠B+∠BAD=90°,据此证明;
(3)①当AE平分∠CAB时,则2∠EAB+∠B=90°,∠CAE=∠FAE,∠ACE=∠AFE,证明△ACE≌△AFE,得到AE=AC=3,则BF=2,设CE=a,则EF=a,BE=4-a,由勾股定理可求出a的值,进而可得BE;②当∠CAE=∠B时,作点A关于BC的对称点H,连接AE、HE,并延长HE交AB于点F,设∠CAE=x,则∠ABC=x,∠AHE=∠CAE=x,∠CEH=∠BEF,则∠BEF+∠ABC=90°,根据等面积法可得HF,然后利用勾股定理可得AF,设AE=HE=a,利用勾股定理可得a的值,进而可得CE、BE的值.
一、选择题
1.如图,直线,一直角三角板ABC(∠ACB=90° )放在平行线上,两直角边分别l1与l2、交于点D、E,现测得∠1=75°,则∠2的度数为( )
A.15° B.25° C.30° D.35°
2.对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )
A.a=﹣3,b=2 B.a=3,b=2 C.a=3,b=﹣1 D.a=﹣1,b=3
3.如图,下列条件中,一定能判断的是( )
A. B. C. D.
4.下列命题中,是假命题的是( )
A.平面内,若ab,a⊥c,那么b⊥c
B.两直线平行,同位角相等
C.负数的平方根是负数
D.若,则a=b
5.已知在中,,,则的度数是( )
A. B. C. D.
6.如图,在平面直角坐标系中,,,,,…根据这个规律,点的坐标是( )
A. B. C. D.
7.能说明命题“一个钝角与一个锐角的差一定是锐角”是假命题的反例是( )
A. B.
C. D.
8.如图,给出下列条件.①;②;③,且;④其中,能推出的条作为( )
A.①②③ B.①②④ C.①③④ D.②③④
9.如图,,平分,D是的中点,,则( )
A. B. C. D.
10.已知等腰三角形一腰上的高与另一腰的夹角为,那么这个等腰三角形的顶角等于( )
A.或 B. C. D.或
二、填空题
11.如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着 的展开式 的系数;第五行的五个数恰好对应着 的展开式 的系数;根据数表中前五行的数字所反映的规律,则 .
12.将“同角的补角相等”改写成“如果……那么……”的形式为 .
13.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
14.等腰中,,平分,若,则 .
三、解答题
15.如图,已知,则,,之间的关系是: ▲ ,请写出你的证明过程.
16.判断下列命题的真假,若是假命题,请举出反例;若是真命题,请给出证明.
若 ,则 ;
三个角对应相等的两个三角形全等.
17.如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.
18.在中,,求的度数.
四、综合题
19.如图,已知四个关系式:①AC=DC;②BC=EC;③∠DCA=∠ECB:④AB=DE.
(1)从上面四个关系式中任取三个为条件,余下的一个为结论,组成一个命题.在组成的命题中真命题的个数是 ;
(2)从(1)中选择一个真命题进行证明
已知:
求证:
证明:
20.如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得,连接.
(1)求证:;
(2)若,连接平分平分,求的度数.
21.一个角的余角的两倍称为这个角的倍余角.
(1)若,∠2是∠1的倍余角,则∠2的度数为 ;若,∠2是∠1的倍余角,则∠2的度数为 ;(用的代数式表示)
(2)如图1,在△ABC中,,在AC上截取,在AB上截取.求证:∠ABC是∠EDB的倍余角;
(3)如图2,在(2)的情况下,作交AC于点F,将△BFC沿BF折叠得到,交AC于点P,若,设,求∠CPB的度数.
22.定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为,那么称此三角形为“倍角互余三角形”.
(1)【基础巩固】若是“倍角互余三角形”,,,则 ;
(2)【尝试应用】如图1,在中,,点为线段上一点,若与互余.求证:是“倍角互余三角形”;
(3)【拓展提高】如图2,在中,,,,试问在边上是否存在点,使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:如图,过点C作CF∥l1,
∵l1∥l2,
∴CF∥l1∥l2,
∴∠FCD=∠1=75°,∠BCF=∠2,
∵∠ACB=90°,
∴∠1+∠2=90°,
∴∠2=90°-75°=15°,
故答案为:A.
【分析】过点C作CF∥l1,根据平行公理得出CF∥l1∥l2,得出∠FCD=∠1=75°,∠BCF=∠2,再根据∠ACB=90°得出∠1+∠2=90°,即可得出∠2=90°-75°=15°.
2.【答案】A
【解析】【解答】解:A、a=-3,b=2,满足a2>b2,a<b,能说明命题是假命题;
B、a=3,b=2,满足a2>b2,a>b,不能说明命题是假命题;
C、a=3,b= 1,满足a2>b2,a>b,不能说明命题是假命题;
D、a= 1,b=3,不满足a2>b2,不能说明命题是假命题.
故答案为:A.
【分析】通过计算判定,满足a2>b2,不满足a>b即可.
3.【答案】B
【解析】【解答】解:A、∠2与∠3不是两条直线被第三条直线所截形成的角,所以即使相等也不能判断AB∥CD,故本选项错误;
B、∠1与∠2是AB、CD两条直线被第三条直线所截形成的内错角,根据内错角相等,两直线平行,可得AB∥CD,故本选项正确;
C、∠4与∠5不是两条直线被第三条直线所截形成的角,所以即使相等也不能判断AB∥CD,故本选项错误;
D、∠3与∠4是AB、CD两条直线被第三条直线所截形成的同旁内角,即使相等,也不能判断AB∥CD,故本选项错误.
故答案为:B.
【分析】两条直线被第三条直线所截形成同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,据此判断.
4.【答案】C
【解析】【解答】解:A、平面内,若a∥b,a⊥c,那么b⊥c,是真命题,不符合题意;
B、两直线平行,同位角相等,是真命题,不符合题意;
C、负数没有平方根,故本说法是假命题,符合题意;
D、若,则a=b,是真命题,不符合题意.
故答案为:C.
【分析】根据二直线平行,同位角相等及垂直的定义即可判断A;根据平行线的性质,可判断B;根据负数没有平方根可判断C;根据算术平方根的双重非负性可判断D.
5.【答案】B
【解析】【解答】解:在中,,,
,
故答案为:B.
【分析】直接根据内角和定理计算即可.
6.【答案】C
【解析】【解答】解:观察图形可知,横坐标依次为1、2、3、4、、n,纵坐标依次为-2、0、2、0、,四个一循环,
∵,
∴点的坐标是.
故答案为:C
【分析】先求出规律,再结合,即可得到点的坐标是。
7.【答案】D
【解析】【解答】解:A、是锐角,不符合题意;
B、与是两个锐角,不符合题意;
C、是锐角,不符合题意;
D、是钝角,符合题意.
故答案为:D.
【分析】原命题为假命题时,应满足一个钝角与一个锐角的差不是锐角,据此判断.
8.【答案】C
【解析】【解答】解:①∵,
∴,正确,符合题意;
②∵,
∴,(内错角相等,两直线平行),选项不符合题意;
③∵,,
∴,
∴,正确,符合题意;
④∵,
∴,由同位角相等,两直线平行可得,正确,符合题意;
故能推出的条件为①③④.
故答案为:C.
【分析】两条直线被第三条直线所截,如果同位角相等,那么被截的两直线平行;两条直线被第三条直线所截,如果内错角相等,那么被截的两直线平行;两条直线被第三条直线所截,如果同旁内角互补,那么被截的两直线平行;从而一一判断即可得出答案.
9.【答案】B
【解析】【解答】解:∵CB平分∠ACE,∠ACE=110°
∴∠BCE=∠BCA=55°
∵CE//AB
∴∠BCE=∠B=55°
∴∠BCA=∠B=55°
∴AC=AB
∵D为BC中点
∴AD⊥BC,即∠ADB=90°
∴∠DAB=180°-∠B-∠ADB=180°-55°-90°=35°
故答案为:B.
【分析】根据角平分线的性质和平行线的性质,可以得出∠BCA=∠B=55°,从而得到AB=AC,再由点D是BC中点,跟等腰三角形三线合一的性质可知∠ADB=90°,最后根据∠DAB=180°-∠B-∠ADB,即可求解.
10.【答案】A
【解析】【解答】解:
如图(1),当是锐角三角形时,
,,
,
,
;
如图(2),当是钝角三角形时,
,,
,
,
,;
综上所述,它的顶角度数为:或,
故答案为:A.
【分析】分两种情况:①当是锐角三角形时,②当是钝角三角形时,再分别画出图象并利用三角形的内角和及等腰三角形的性质求解即可。
11.【答案】a5+5a4b+10a3b2+10a2b3+5ab4+b5
【解析】【解答】由图形可得
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
∴答案为:a5+5a4b+10a3b2+10a2b3+5ab4+b5.
【分析】观察图表寻找规律:三角形是一个由数字排列成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
12.【答案】如果两个角是同一个角的补角,那么这两个角相等
【解析】【解答】解:将“同角的补角相等”改写成“如果……那么……”的形式为
如果两个角是同一个角的补角,那么这两个角相等.
故答案为:如果两个角是同一个角的补角,那么这两个角相等
【分析】要将一个命题写成“如果……那么……”的形式,就要分清命题的题设和结论,如果后面是题设,那么的后面是结论,即可求解.
13.【答案】20°
【解析】【解答】解:过点C作CF∥AE,
∵AE∥BD,
∴AE∥BD∥CF,
∴∠2=∠DCF=30°,∠EAC+∠ACF=180°,
∵∠1=∠EAC=130°,
∴∠ACF=∠ACE+∠DCF=180°-130°=50°,
∴∠ACE=50°-30°=20°.
故答案为:20°
【分析】过点C作CF∥AE,利用同平行与一条直线的两直线平行,可证得AE∥BD∥CF,利用平行线的性质可求出∠DCF的度数,同时可证得∠EAC+∠ACF=180°,由此可求出∠ACF的度数,即可求出∠ACE的度数.
14.【答案】100°
【解析】【解答】解:如图所示,
∵AB=AC,
∴∠C=∠ABC,
又∵BD平分∠ABC,
∴∠1=∠2=∠ABC,
∴∠C=2∠1,
∵∠2+∠C=180°-∠BDC,且∠BDC=120°,
∴3∠1=60°,即∠1=∠2=20°,
又∵∠BDC=∠A+∠1,
∴∠A=∠BDC-∠1=120°-20°=100°.
故答案为:100°.
【分析】由AB=AC,根据等边对等角,可得∠ABC=∠C,又由BD平分∠ABC,∠BDC=120°,可求得∠1的度数,然后根据三角形内角和定理,即可求得∠A的度数.
15.【答案】结论:∠APC=∠A+∠C.
证明:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A=∠APE,∠C=∠CPE,
∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C.
【解析】【分析】过点P作PE∥AB,利用在同一个平面内,同平行于一条直线的两直线平行,可证得PE∥AB∥CD,利用平行线的性质可推出∠A=∠APE,∠C=∠CPE;然后根据∠APC=∠APE+∠CPE,可得到∠A,∠C,∠APC之间的关系.
16.【答案】解: 若 ,则 是假命题,
例如: , ,
,但 ;
三个角对应相等的两个三角形全等是假命题,
例如:两个边长不相等的等边三角形不全等.
【解析】【分析】(1)可以用特殊值法:取 , 进行判断即可.(2)可以举反例说明, 例如:两个边长不相等的等边三角形不全等.
17.【答案】证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在和中,
,
∴,
∴,
∴AC∥DF.
【解析】【分析】根据BE=CF以及线段的和差关系可得BC=EF,由已知条件可知AB=DE,∠ABC=∠DEF,利用SAS证明△ABC≌△DEF,得到∠ACB=∠F,然后根据平行线的判定定理进行证明.
18.【答案】解:设,则,
∵,
∴,
解得,
∴.
【解析】【分析】设,则,利用三角形的内角和可得,再求出x的值即可。
19.【答案】(1)2
(2)解:若选①②③为条件,④为结论,
已知:AC=DC,BC=EC,∠DCA=∠ECB.
求证:AB=DE.
证明:∵∠DCA=∠ECB,
∴∠DCA+∠ACE=∠BCE+∠ACE,即∠ACB=∠DCE,
在△ACB和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE.
【解析】【解答】解:(1)若①②③为条件,④为结论,
则可利用SAS证明△ACB≌△DCE,可得④;
若①②④为条件,③为结论,
则可利用SSS证明△ACB≌△DCE,可得③;
若①③④为条件,②为结论,
无法证明△ACB≌△DCE,则不可得②;
若②③④为条件,①为结论,
无法证明△ACB≌△DCE,则不可得①;
∴真命题的个数是2;
【分析】(1)根据真命题的定义求解即可;
(2)结合(1)的条件,利用“SAS”证明△ACB≌△DCE,即可得到AB=DE。
20.【答案】(1)证明:∵E为中点,
∴,
在和中,
,
∴,
∴,
∴;
(2)解:由(1)得:,
∵平分,
∴,
∴,
∵,
∴
【解析】【分析】(1)根据SAS证明△ADE≌△CFE,可得∠A=∠ECF,根据平行线的判定即证;
(2)由(1)知∠A=∠ECF,由角平分线的定义可得,利用等量代换即可求解.
21.【答案】(1)120°;
(2)解:设,
∵CD=CB,AE=AD
∴,
∴,
,
∴即∠ABC是∠EDB的倍余角.
(3)解:由(2)得,
∵,
∴,
∵,
∴,
∴,
∴,.
【解析】【解答】解:(1)∵∠1=30°,∠2是∠1的倍余角,
∴∠2=2(90° 30°)=120°;
∵∠1=α,∠2是∠1的倍余角,
∴∠2=2(90° α)=180° 2α.
故答案为:120°;180° 2α.
【分析】(1)根据∠2是∠1的倍余角可得∠2=2×(90°-∠1),据此解答;
(2)设∠AED=a,∠CBD=b,由等腰三角形的性质可得∠AED=∠ADE=a,∠DBC=∠BDC=b,由内角和定理可得∠EDB=180°-a-b,∠ABC=180°-(180°-2a)-(180°-2b)=2a+2b+180°,甲车证明;
(3)由(2)得∠EDB=45°,根据平行线的性质可得∠EDB=∠DBF=45°,根据等腰三角形的性质可得∠DBC=45°+a=∠BDC,则∠DBP=45°-a,∠DBP+∠DBC=90°,甲车解答.
22.【答案】(1)15
(2)证明:∵,
∴,
又∵,
∴,
∴
∴是倍角互余三角形.
(3)解:①当平分时,则,
∴,
∴,则,
设,则,,
在中,,
解得,所以.
②当时,作点关于的对称点,连接、,并延长交于点.
设,则,
∵点、点关于对称,
∴,
∴,
∴,
即,
利用等积法求得:,
∴,
在中,
设,在中,,
∴,
在中,,
∴,
综上所述,或时,为倍角互余三角形.
【解析】【解答】解:(1)∵是“倍角互余三角形”,,,
∴,
∴,
故答案为:15;
【分析】(1)由题意可得∠A+2∠B=90°,据此计算;
(2)由内角和定理可得∠B+∠CAB=90°,由题意可得∠CAB+∠CAD=90°,则∠B=∠CAD,∠B+∠CAD+∠BAD=2∠B+∠BAD=90°,据此证明;
(3)①当AE平分∠CAB时,则2∠EAB+∠B=90°,∠CAE=∠FAE,∠ACE=∠AFE,证明△ACE≌△AFE,得到AE=AC=3,则BF=2,设CE=a,则EF=a,BE=4-a,由勾股定理可求出a的值,进而可得BE;②当∠CAE=∠B时,作点A关于BC的对称点H,连接AE、HE,并延长HE交AB于点F,设∠CAE=x,则∠ABC=x,∠AHE=∠CAE=x,∠CEH=∠BEF,则∠BEF+∠ABC=90°,根据等面积法可得HF,然后利用勾股定理可得AF,设AE=HE=a,利用勾股定理可得a的值,进而可得CE、BE的值.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
