第六单元 多边形的面积--三角形的面积同步练习 人教版数学五年级上册(有答案)
文档属性
| 名称 | 第六单元 多边形的面积--三角形的面积同步练习 人教版数学五年级上册(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 08:27:37 | ||
图片预览


文档简介
第六单元 多边形的面积--三角形的面积 梯形的面积
一、单选题
1.下图中,面积相等的两个长方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比( )
A.甲的面积大 B.乙的面积大 C.相等
2.两个( )的三角形一定能拼成一个平行四边形。
A.面积相等 B.等高 C.完全一样
3.甲、乙两个三角形面积相等,甲的底是乙的2倍,甲的这条底所对应的高是乙的这条底所对应高的( )。
A.2倍 B.一半 C.相等
4.一个直角三角形,若三条边长分别是3厘米、4厘米、5厘米,则该三角形的面积是( )平方厘米。
A.10 B.7.5 C.6
5.下图中三角形( )的面积可以用“4×3÷2”进行计算。
A. B. C.
6.三角形的底扩大到它的2倍,高不变,它的面积( )
A.扩大到原来的2倍 B.扩大到原来的4倍 C.不变
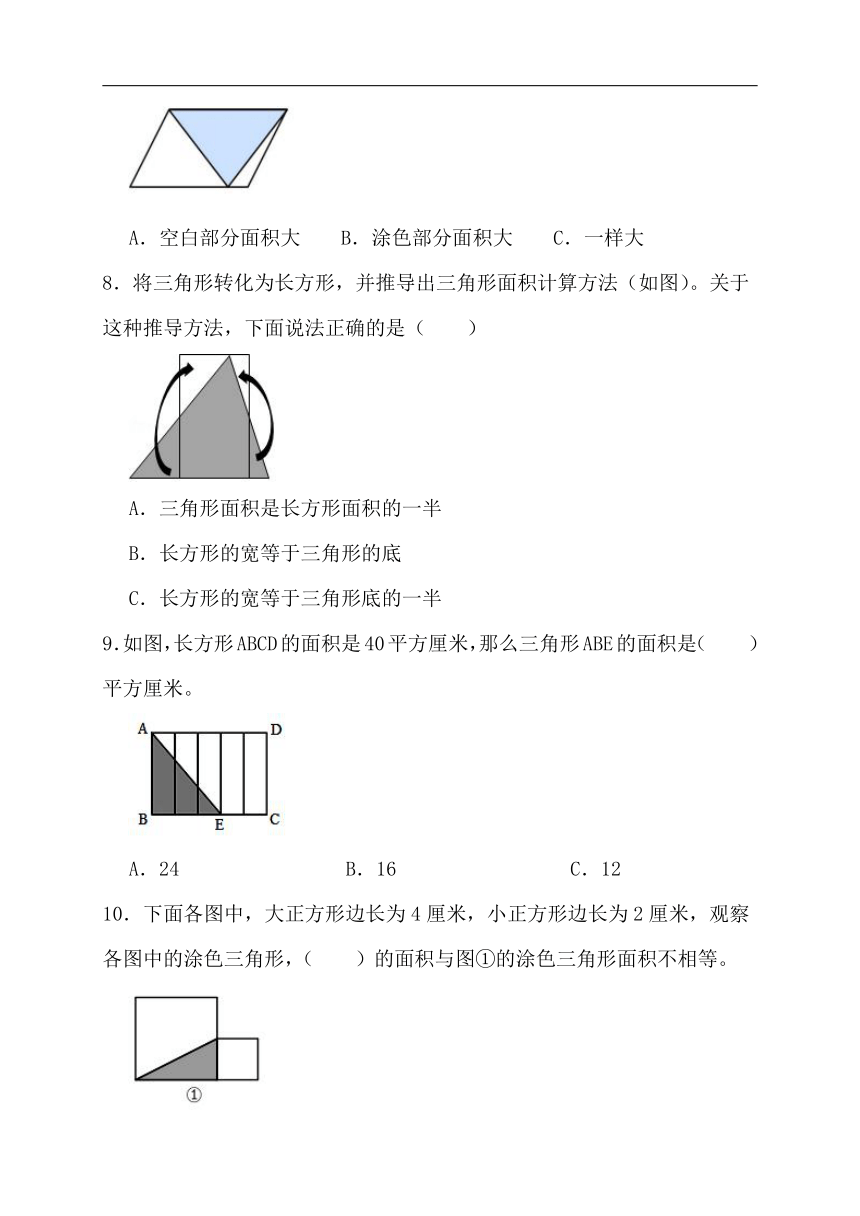
7.在下面的平行四边形中,涂色部分和空白部分的面积相比较,下面说法正确的是( )。
A.空白部分面积大 B.涂色部分面积大 C.一样大
8.将三角形转化为长方形,并推导出三角形面积计算方法(如图)。关于这种推导方法,下面说法正确的是( )
A.三角形面积是长方形面积的一半
B.长方形的宽等于三角形的底
C.长方形的宽等于三角形底的一半
9.如图,长方形ABCD的面积是40平方厘米,那么三角形ABE的面积是( )平方厘米。
A.24 B.16 C.12
10.下面各图中,大正方形边长为4厘米,小正方形边长为2厘米,观察各图中的涂色三角形,( )的面积与图①的涂色三角形面积不相等。
A. B. C.
二、填空题
11.三角形面积= ,用字母表示为S= .
12.一个直角三角形的两条直角边分别是3cm和4cm,斜边长5cm,这个直角三角形的面积是 cm2,斜边上的高是 厘米
13.如图,这是由4个相同的直角三角形拼成的大正方形。已知直角三角形的两条直角边长分别是4cm和6cm,那么大正方形的面积是 cm2。
14.有一块三角形的花圃,它的底是35米,高是18米,这块花圃的面积是 m2;如果每平方米产鲜花20枝,这块花圃一共可以产鲜花 枝。
15.一个三角形的面积是42dm ,底是12dm,高是 dm。
16.一个三角形的面积是20平方厘米,高是2厘米,与这条高对应的底是
厘米。
17.如图是由6个小正方形组成的,已知三角形A的面积是2cm2,则三角形B的面积是 cm2,空白部分的面积是 cm2。
18.如图所示,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20,宽是12,则它内部阴影部分的面积是 。
三、作图题
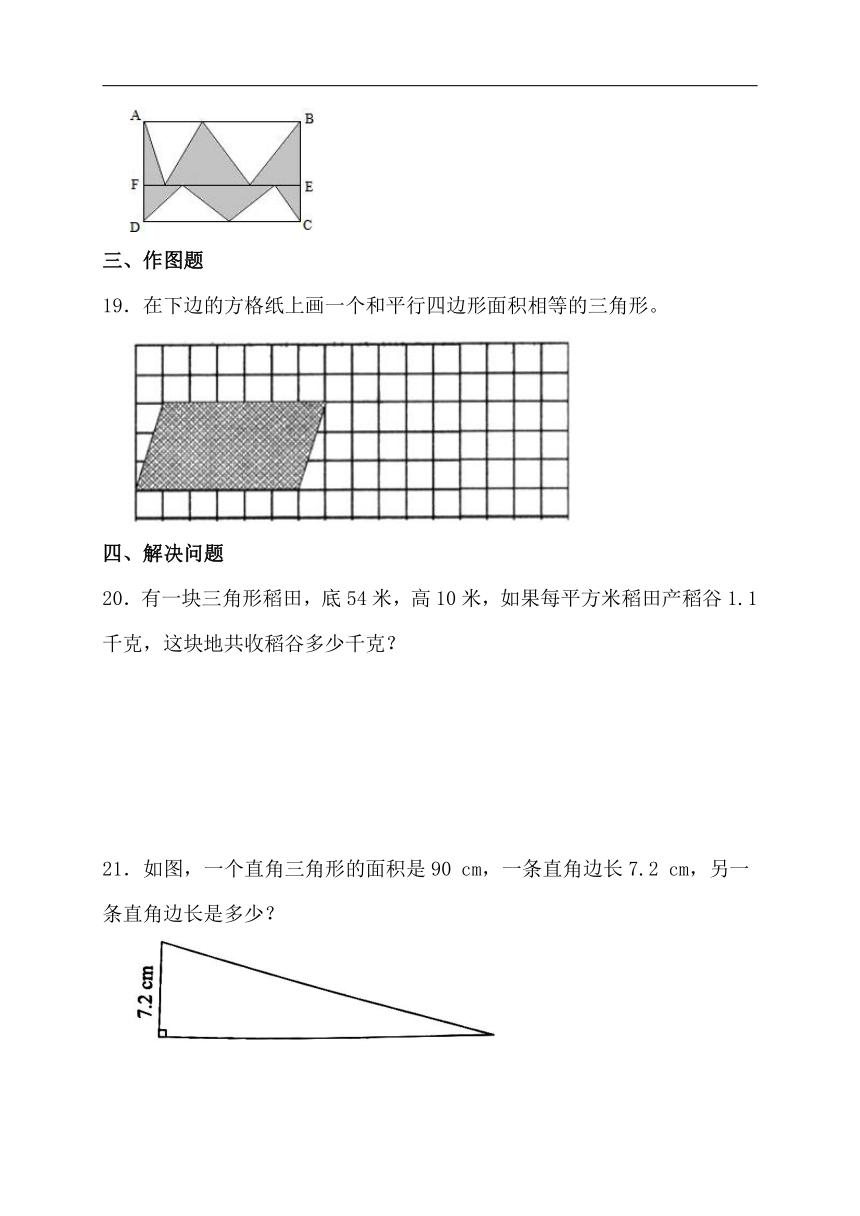
19.在下边的方格纸上画一个和平行四边形面积相等的三角形。
四、解决问题
20.有一块三角形稻田,底54米,高10米,如果每平方米稻田产稻谷1.1千克,这块地共收稻谷多少千克?
21.如图,一个直角三角形的面积是90 cm,一条直角边长7.2 cm,另一条直角边长是多少?
22.一块底是240米,高是90米的三角形稻田,平均每公顷收稻谷22400千克,这块稻田共收水稻多少千克?
23.有一个三角形的底是6米,如果底延长2米,面积就增加4平方米。原来三角形的面积是多少平方米?
24.如图,线段BC长20cm,线段DC长12cm,线段AB长10cm,线段AF长6cm,求阴影部分的面积。
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】底×高× ;ah
12.【答案】6;2.4
13.【答案】52
14.【答案】315;6300
15.【答案】7
16.【答案】20
17.【答案】1;9
18.【答案】120
19.【答案】解:如图所示:(图形不唯一)
20.【答案】解:54×10÷2=270(平方米)
270×1.1=297(千克)
答:这块地共收稻谷297千克。
21.【答案】解:90×2÷7.2
=180÷7.2
=25(cm)
答:另一条直角边长是25cm。
22.【答案】解:240×90÷2
=21600÷2
=10800(平方米)
10800平方米=1.08公顷
1.08×22400=24192(千克)
答:这块稻田共收水稻24192千克。
23.【答案】解:4×2÷2=4(米)
6×4÷2=12(平方米)
答:原来三角形的面积是12平方米。
24.【答案】解:
三角形CDF的面积:12×(10+20)÷2=12×30÷2=180(平方厘米)
三角形CDG的面积:12×20÷2=120(平方厘米)
阴影部分的面积:180-120=60(平方厘米)
答:阴影部分的面积是60平方厘米。
一、单选题
1.下图中,面积相等的两个长方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比( )
A.甲的面积大 B.乙的面积大 C.相等
2.两个( )的三角形一定能拼成一个平行四边形。
A.面积相等 B.等高 C.完全一样
3.甲、乙两个三角形面积相等,甲的底是乙的2倍,甲的这条底所对应的高是乙的这条底所对应高的( )。
A.2倍 B.一半 C.相等
4.一个直角三角形,若三条边长分别是3厘米、4厘米、5厘米,则该三角形的面积是( )平方厘米。
A.10 B.7.5 C.6
5.下图中三角形( )的面积可以用“4×3÷2”进行计算。
A. B. C.
6.三角形的底扩大到它的2倍,高不变,它的面积( )
A.扩大到原来的2倍 B.扩大到原来的4倍 C.不变
7.在下面的平行四边形中,涂色部分和空白部分的面积相比较,下面说法正确的是( )。
A.空白部分面积大 B.涂色部分面积大 C.一样大
8.将三角形转化为长方形,并推导出三角形面积计算方法(如图)。关于这种推导方法,下面说法正确的是( )
A.三角形面积是长方形面积的一半
B.长方形的宽等于三角形的底
C.长方形的宽等于三角形底的一半
9.如图,长方形ABCD的面积是40平方厘米,那么三角形ABE的面积是( )平方厘米。
A.24 B.16 C.12
10.下面各图中,大正方形边长为4厘米,小正方形边长为2厘米,观察各图中的涂色三角形,( )的面积与图①的涂色三角形面积不相等。
A. B. C.
二、填空题
11.三角形面积= ,用字母表示为S= .
12.一个直角三角形的两条直角边分别是3cm和4cm,斜边长5cm,这个直角三角形的面积是 cm2,斜边上的高是 厘米
13.如图,这是由4个相同的直角三角形拼成的大正方形。已知直角三角形的两条直角边长分别是4cm和6cm,那么大正方形的面积是 cm2。
14.有一块三角形的花圃,它的底是35米,高是18米,这块花圃的面积是 m2;如果每平方米产鲜花20枝,这块花圃一共可以产鲜花 枝。
15.一个三角形的面积是42dm ,底是12dm,高是 dm。
16.一个三角形的面积是20平方厘米,高是2厘米,与这条高对应的底是
厘米。
17.如图是由6个小正方形组成的,已知三角形A的面积是2cm2,则三角形B的面积是 cm2,空白部分的面积是 cm2。
18.如图所示,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20,宽是12,则它内部阴影部分的面积是 。
三、作图题
19.在下边的方格纸上画一个和平行四边形面积相等的三角形。
四、解决问题
20.有一块三角形稻田,底54米,高10米,如果每平方米稻田产稻谷1.1千克,这块地共收稻谷多少千克?
21.如图,一个直角三角形的面积是90 cm,一条直角边长7.2 cm,另一条直角边长是多少?
22.一块底是240米,高是90米的三角形稻田,平均每公顷收稻谷22400千克,这块稻田共收水稻多少千克?
23.有一个三角形的底是6米,如果底延长2米,面积就增加4平方米。原来三角形的面积是多少平方米?
24.如图,线段BC长20cm,线段DC长12cm,线段AB长10cm,线段AF长6cm,求阴影部分的面积。
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】底×高× ;ah
12.【答案】6;2.4
13.【答案】52
14.【答案】315;6300
15.【答案】7
16.【答案】20
17.【答案】1;9
18.【答案】120
19.【答案】解:如图所示:(图形不唯一)
20.【答案】解:54×10÷2=270(平方米)
270×1.1=297(千克)
答:这块地共收稻谷297千克。
21.【答案】解:90×2÷7.2
=180÷7.2
=25(cm)
答:另一条直角边长是25cm。
22.【答案】解:240×90÷2
=21600÷2
=10800(平方米)
10800平方米=1.08公顷
1.08×22400=24192(千克)
答:这块稻田共收水稻24192千克。
23.【答案】解:4×2÷2=4(米)
6×4÷2=12(平方米)
答:原来三角形的面积是12平方米。
24.【答案】解:
三角形CDF的面积:12×(10+20)÷2=12×30÷2=180(平方厘米)
三角形CDG的面积:12×20÷2=120(平方厘米)
阴影部分的面积:180-120=60(平方厘米)
答:阴影部分的面积是60平方厘米。
