25.2用列举法求概率(第4课时)[上学期]
文档属性
| 名称 | 25.2用列举法求概率(第4课时)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 385.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-16 00:00:00 | ||
图片预览

文档简介
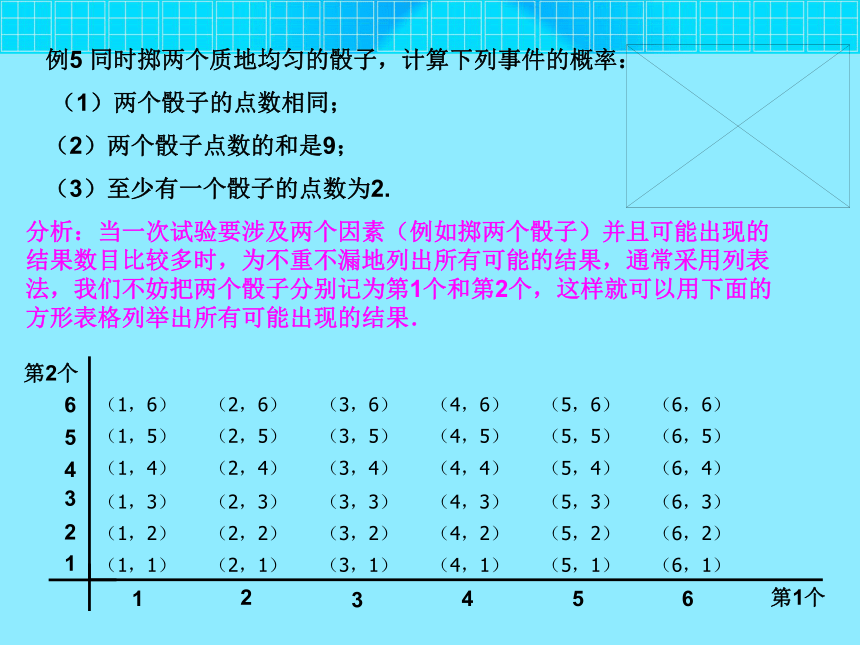
课件7张PPT。义务教育课程标准实验教科书九年级 上册人民教育出版社25.2 用列举法求概率(第4课时) 例5 同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同;
(2)两个骰子点数的和是9;
(3)至少有一个骰子的点数为2.
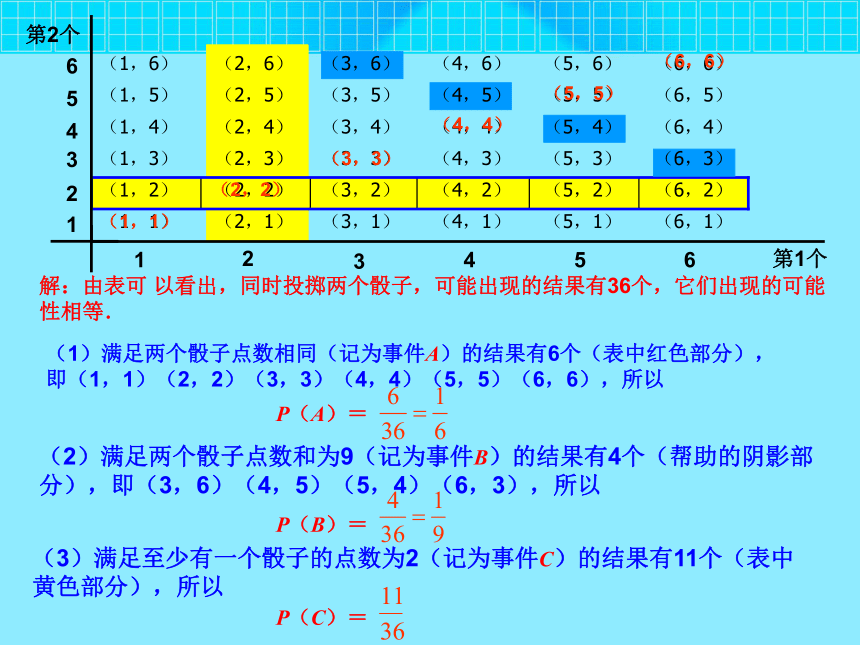
分析:当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目比较多时,为不重不漏地列出所有可能的结果,通常采用列表法,我们不妨把两个骰子分别记为第1个和第2个,这样就可以用下面的方形表格列举出所有可能出现的结果.123456123456第1个第2个(2)满足两个骰子点数和为9(记为事件B)的结果有4个(帮助的阴影部分),即(3,6)(4,5)(5,4)(6,3),所以(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个(表中黄色部分),所以解:由表可 以看出,同时投掷两个骰子,可能出现的结果有36个,它们出现的可能性相等.123456123456第1个第2个(1)满足两个骰子点数相同(记为事件A)的结果有6个(表中红色部分),即(1,1)(2,2)(3,3)(4,4)(5,5)(6,6),所以P(A)=P(B)=P(C)=如果把例5中的“同时掷两个骰子“改为”把一个骰子掷两次”,所得到的结果有变化吗? 没 有 变 化 请你计算试一试1. 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”,小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并且自由转动图中的转盘(转盘被分成相等的三个扇形) 如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜,求游戏者获胜的概率.练习总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有1种;(1,1),因此游戏者获胜的概率为( 1 , 1 )( 1 , 2 )( 1 , 3 )( 2 , 1 )( 2 , 2 )( 2 , 3 )解:每次游戏时,所有可能出现的结果如下:2. 在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,再随机地抽取一张.那么第二次取出的数字能够整除第一次取出的数字的概率是多少?由列表可以看出:共有14个第二次取出的数字能够整除第一次取出的数字:因此: 所求的概率为:
(1)两个骰子的点数相同;
(2)两个骰子点数的和是9;
(3)至少有一个骰子的点数为2.
分析:当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目比较多时,为不重不漏地列出所有可能的结果,通常采用列表法,我们不妨把两个骰子分别记为第1个和第2个,这样就可以用下面的方形表格列举出所有可能出现的结果.123456123456第1个第2个(2)满足两个骰子点数和为9(记为事件B)的结果有4个(帮助的阴影部分),即(3,6)(4,5)(5,4)(6,3),所以(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个(表中黄色部分),所以解:由表可 以看出,同时投掷两个骰子,可能出现的结果有36个,它们出现的可能性相等.123456123456第1个第2个(1)满足两个骰子点数相同(记为事件A)的结果有6个(表中红色部分),即(1,1)(2,2)(3,3)(4,4)(5,5)(6,6),所以P(A)=P(B)=P(C)=如果把例5中的“同时掷两个骰子“改为”把一个骰子掷两次”,所得到的结果有变化吗? 没 有 变 化 请你计算试一试1. 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”,小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并且自由转动图中的转盘(转盘被分成相等的三个扇形) 如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜,求游戏者获胜的概率.练习总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有1种;(1,1),因此游戏者获胜的概率为( 1 , 1 )( 1 , 2 )( 1 , 3 )( 2 , 1 )( 2 , 2 )( 2 , 3 )解:每次游戏时,所有可能出现的结果如下:2. 在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,再随机地抽取一张.那么第二次取出的数字能够整除第一次取出的数字的概率是多少?由列表可以看出:共有14个第二次取出的数字能够整除第一次取出的数字:因此: 所求的概率为:
同课章节目录
