1.3.2 空间向量运算的坐标表示 课件(共18张PPT)
文档属性
| 名称 | 1.3.2 空间向量运算的坐标表示 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 09:44:14 | ||
图片预览






文档简介
(共18张PPT)
1.3.2空间向量运算
的坐标表示
复习导入
空间直角坐标系
空间直角坐标系
空间向量的坐标表示
空间向量基本定理
不共面,则对,唯一有序实数组,使得
点的坐标
向量的坐标
复习导入
名 称 坐 标 表 示
加法
减法
数乘
数量积
模长
夹角
平行
垂直
平面向量运算的坐标表示
设,
类比平面向量坐标运算,你能得出空间向量坐标运算并给出证明吗?
新知探究
设
与平面向量运算的坐标表示一样,我们有:
空间向量运算的坐标表示
如何证明?
新知探究
空间向量运算的坐标表示
下面我们证明空间向量数量积运算的坐标表示.
设则
所以
利用向量数量积的分配律以及
得,
其他运算类似可证,请同学们自主完成。
新知探讨
名 称 坐 标 表 示
加法
减法
数乘
数量积
模长
夹角
平行 当时
垂直
空间向量运算的坐标表示
设
新知探讨
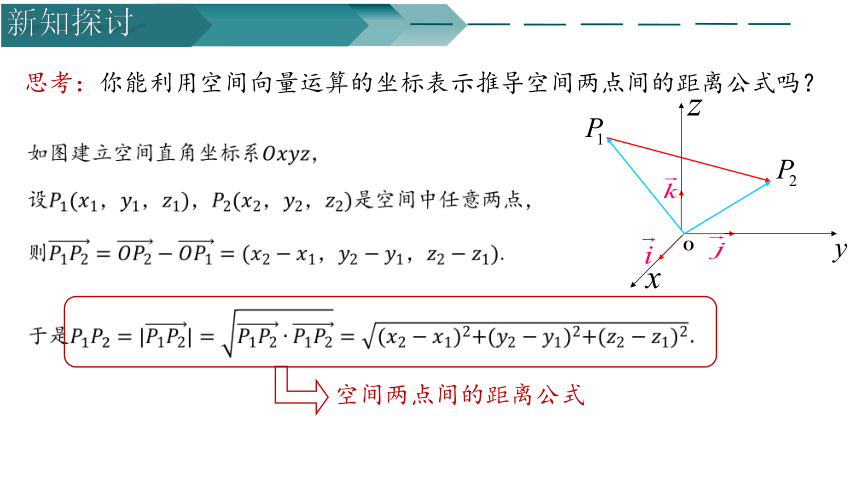
思考:你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
O
如图建立空间直角坐标系,
设,是空间中任意两点,
则.
于是.
空间两点间的距离公式
例题讲解
练习1.已知,求:
(1) +,-,·,
(2)(2)·(-),(+)·(-).
解(1):
;
;
.
(2): (2)(-) ;
(+)(-).
例题讲解
例2.如图,在正方体中,分别是,的中点.
求证.
证明:不妨设正方体的棱长为1,
建立如图所示的空间直角坐标系,
则所以.
又,,所以.
所以.
所以,即.
例题讲解
例3.如图,在棱长为1的正方体中,为的中点,分别在棱,上,,.
(1)求的长.(2)求与所成角的余弦值.
解(1):建立如图所示的空间直角坐标系,
则点的坐标为点的坐标为.
于是.
例题讲解
例3.如图,在棱长为1的正方体中,为的中点,分别在棱,上,,.
(1)求的长.(2)求与所成角的余弦值.
解(2):由已知,得,
,,
所以,
所以
所以
所以,与所成角的余弦值是.
例题讲解
练习2.已知空间三点,,,设=,
=,若向量+与-2互相垂直,求的值.
解:,
,
∴+,
.
∵ +与互相垂直,
∴,即,
.
例题讲解
练习3.已知空间三点.设,.若与互相平行,求.
解:∵,
,
∴
∵与平行,所以,
即,所以
则或.
例题讲解
练习4.已知,分别在以下情形下求实数的值.
(1); (2).
解: (1),
,所以,解得
(2)
,
即,解得
例题讲解
练习5.已知空间三点.
求:(1)向量,的模;(2)向量,夹角的余弦值.
解: (1)∵
∴
(2) ∵
∴.
例题讲解
练习6.如图,,原点是的中点,点的坐标为,点在平面上,且, ,求
(1)向量的坐标;(2)向量,夹角的余弦值.
解: (1)过作于,则,
,
所以点坐标为,
又因为 ,
所以.
例题讲解
练习6.如图,,原点是的中点,点的坐标为,点在平面上,且, ,求
(1)向量的坐标;(2)向量,夹角的余弦值.
解: (2)因为, ,
, ,
所以, ,
则, ,
所以
小结
名 称 坐 标 表 示
加法
减法
数乘
数量积
模长
夹角
平行 当时
垂直
1.3.2空间向量运算
的坐标表示
复习导入
空间直角坐标系
空间直角坐标系
空间向量的坐标表示
空间向量基本定理
不共面,则对,唯一有序实数组,使得
点的坐标
向量的坐标
复习导入
名 称 坐 标 表 示
加法
减法
数乘
数量积
模长
夹角
平行
垂直
平面向量运算的坐标表示
设,
类比平面向量坐标运算,你能得出空间向量坐标运算并给出证明吗?
新知探究
设
与平面向量运算的坐标表示一样,我们有:
空间向量运算的坐标表示
如何证明?
新知探究
空间向量运算的坐标表示
下面我们证明空间向量数量积运算的坐标表示.
设则
所以
利用向量数量积的分配律以及
得,
其他运算类似可证,请同学们自主完成。
新知探讨
名 称 坐 标 表 示
加法
减法
数乘
数量积
模长
夹角
平行 当时
垂直
空间向量运算的坐标表示
设
新知探讨
思考:你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
O
如图建立空间直角坐标系,
设,是空间中任意两点,
则.
于是.
空间两点间的距离公式
例题讲解
练习1.已知,求:
(1) +,-,·,
(2)(2)·(-),(+)·(-).
解(1):
;
;
.
(2): (2)(-) ;
(+)(-).
例题讲解
例2.如图,在正方体中,分别是,的中点.
求证.
证明:不妨设正方体的棱长为1,
建立如图所示的空间直角坐标系,
则所以.
又,,所以.
所以.
所以,即.
例题讲解
例3.如图,在棱长为1的正方体中,为的中点,分别在棱,上,,.
(1)求的长.(2)求与所成角的余弦值.
解(1):建立如图所示的空间直角坐标系,
则点的坐标为点的坐标为.
于是.
例题讲解
例3.如图,在棱长为1的正方体中,为的中点,分别在棱,上,,.
(1)求的长.(2)求与所成角的余弦值.
解(2):由已知,得,
,,
所以,
所以
所以
所以,与所成角的余弦值是.
例题讲解
练习2.已知空间三点,,,设=,
=,若向量+与-2互相垂直,求的值.
解:,
,
∴+,
.
∵ +与互相垂直,
∴,即,
.
例题讲解
练习3.已知空间三点.设,.若与互相平行,求.
解:∵,
,
∴
∵与平行,所以,
即,所以
则或.
例题讲解
练习4.已知,分别在以下情形下求实数的值.
(1); (2).
解: (1),
,所以,解得
(2)
,
即,解得
例题讲解
练习5.已知空间三点.
求:(1)向量,的模;(2)向量,夹角的余弦值.
解: (1)∵
∴
(2) ∵
∴.
例题讲解
练习6.如图,,原点是的中点,点的坐标为,点在平面上,且, ,求
(1)向量的坐标;(2)向量,夹角的余弦值.
解: (1)过作于,则,
,
所以点坐标为,
又因为 ,
所以.
例题讲解
练习6.如图,,原点是的中点,点的坐标为,点在平面上,且, ,求
(1)向量的坐标;(2)向量,夹角的余弦值.
解: (2)因为, ,
, ,
所以, ,
则, ,
所以
小结
名 称 坐 标 表 示
加法
减法
数乘
数量积
模长
夹角
平行 当时
垂直
