1.3.1 空间直角坐标系 课件(共13张PPT)
文档属性
| 名称 | 1.3.1 空间直角坐标系 课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 09:44:44 | ||
图片预览



文档简介
(共13张PPT)
1.3.1空间直角坐标系
复习导入
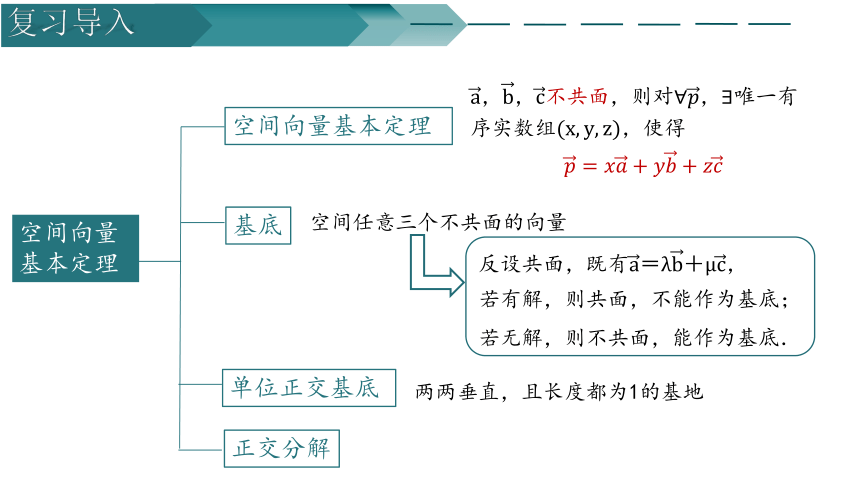
空间向量基本定理
基底
空间向量基本定理
单位正交基底
正交分解
不共面,则对,唯一有序实数组,使得
空间任意三个不共面的向量
反设共面,,
若有解,则共面,不能作为基底;
若无解,则不共面,能作为基底.
两两垂直,且长度都为1的基地
复习导入
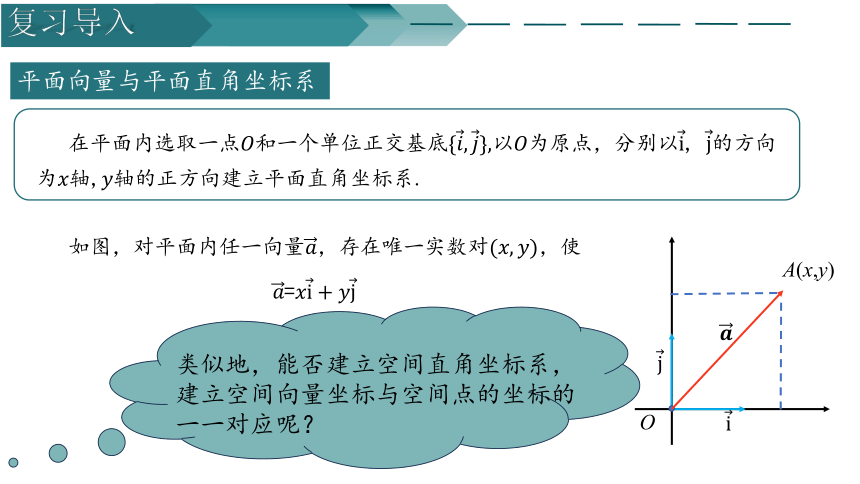
平面向量与平面直角坐标系
在平面内选取一点和一个单位正交基底以为原点,分别以, 的方向为轴,轴的正方向建立平面直角坐标系.
O
A(x,y)
如图,对平面内任一向量,存在唯一实数对,使 =
类似地,能否建立空间直角坐标系,建立空间向量坐标与空间点的坐标的一一对应呢?
新知探究
原 点 坐 标 轴 单 位 长
平 面
空 间
原点
原点
两条相互垂直的数轴:轴、轴
三条两两垂直的数轴、轴
单位长度为
单位长度为
空间直角坐标系,其中为单位正交基底,为原点,坐标轴为轴、轴、轴,坐标平面为平面, 平面,平面.
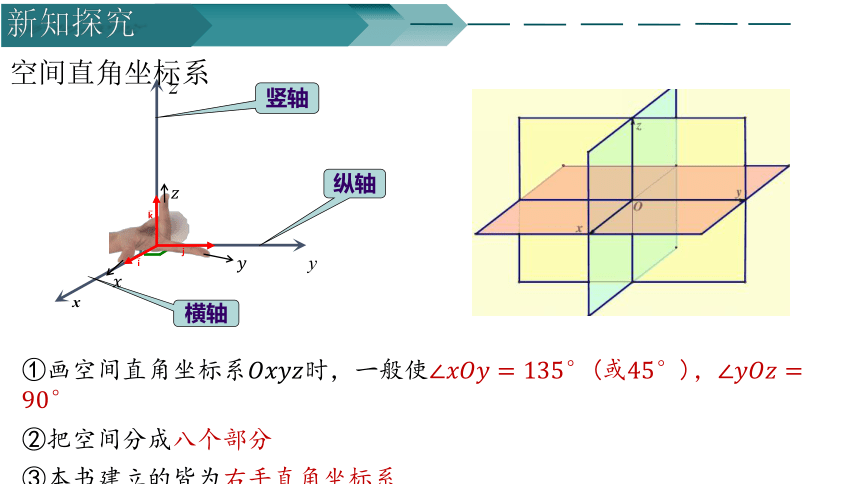
空间直角坐标系
新知探究
横轴
纵轴
竖轴
空间直角坐标系
①画空间直角坐标系时,一般使(或),
②把空间分成八个部分
③本书建立的皆为右手直角坐标系
新知探究
思考:在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?
由空间向量基本定理,
存在唯一的有序实数组,使.
点在空间直角坐标系中的坐标:
:横坐标; :纵坐标; :竖坐标
既可以表示向量,也可以表示点
向量的坐标表示为
=
例题讲解
例1.如图,在长方体中,以为单位正交基底,建立如图所示的空间直角坐标系.
(1)写出四点的坐标;
(2)写出向量,,,的坐标.
解(1):因为,所以,
因为,所以,
点在轴,轴,轴上的射影分别为, 且在坐标轴上的坐标分别为, 所以
点在轴,轴,轴上的射影分别为, 且在坐标轴上的坐标分别为, 所以.
例题讲解
例1.如图,在长方体中,以为单位正交基底,建立如图所示的空间直角坐标系.
(1)写出四点的坐标;
(2)写出向量,,,的坐标.
解(2):,
.
例题讲解
变式1.已知在直三棱柱中,,,为中点, 为中点,建立适当的空间直角坐标系,求向量, , 的坐标
解:建立如图所示的空间直角坐标系
设, ,
,
,
.
例题讲解
变式2.如图所示,垂直于正方形所在的平面,分别是的中点,并且.试建立适当的空间直角坐标系,求向量的坐标.
解:∵,平面,,
∴,,是两两垂直的单位向量.
∴如图建立空间直角坐标系,设,,
∵
∴.
例题讲解
练习1.如图一个正方体,若以为坐标原点,以棱,,所在的直线分别为轴、轴、轴,取正方体的棱长为单位长度,建立空间直角坐标系,则
①顶点, 的坐标分别为________________;
②棱中点的坐标为___________;
③正方形对角线的交点的坐标为___________;
④顶点关于轴对称的点的坐标为________________;
⑤顶点关于平面对称的点的坐标为________________;
⑥顶点关于点对称的点的坐标为________________.
i
j
O
k
x
y
z
A
B
C
D
C1
A1
B1
D1
(0,0,0),(0,1,1)
例题讲解
练习2.在空间直角坐标系中,点关于点的对称点的坐标是( )
. . . .
析:设所求对称点为,则点为线段的中点,
类比直角坐标系中的中点坐标公式可得
解得,
故选
小结
空间直角坐标系
空间直角坐标系
空间向量的坐标表示
空间向量基本定理
不共面,则对,唯一有序实数组,使得
点的坐标
向量的坐标
1.3.1空间直角坐标系
复习导入
空间向量基本定理
基底
空间向量基本定理
单位正交基底
正交分解
不共面,则对,唯一有序实数组,使得
空间任意三个不共面的向量
反设共面,,
若有解,则共面,不能作为基底;
若无解,则不共面,能作为基底.
两两垂直,且长度都为1的基地
复习导入
平面向量与平面直角坐标系
在平面内选取一点和一个单位正交基底以为原点,分别以, 的方向为轴,轴的正方向建立平面直角坐标系.
O
A(x,y)
如图,对平面内任一向量,存在唯一实数对,使 =
类似地,能否建立空间直角坐标系,建立空间向量坐标与空间点的坐标的一一对应呢?
新知探究
原 点 坐 标 轴 单 位 长
平 面
空 间
原点
原点
两条相互垂直的数轴:轴、轴
三条两两垂直的数轴、轴
单位长度为
单位长度为
空间直角坐标系,其中为单位正交基底,为原点,坐标轴为轴、轴、轴,坐标平面为平面, 平面,平面.
空间直角坐标系
新知探究
横轴
纵轴
竖轴
空间直角坐标系
①画空间直角坐标系时,一般使(或),
②把空间分成八个部分
③本书建立的皆为右手直角坐标系
新知探究
思考:在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?
由空间向量基本定理,
存在唯一的有序实数组,使.
点在空间直角坐标系中的坐标:
:横坐标; :纵坐标; :竖坐标
既可以表示向量,也可以表示点
向量的坐标表示为
=
例题讲解
例1.如图,在长方体中,以为单位正交基底,建立如图所示的空间直角坐标系.
(1)写出四点的坐标;
(2)写出向量,,,的坐标.
解(1):因为,所以,
因为,所以,
点在轴,轴,轴上的射影分别为, 且在坐标轴上的坐标分别为, 所以
点在轴,轴,轴上的射影分别为, 且在坐标轴上的坐标分别为, 所以.
例题讲解
例1.如图,在长方体中,以为单位正交基底,建立如图所示的空间直角坐标系.
(1)写出四点的坐标;
(2)写出向量,,,的坐标.
解(2):,
.
例题讲解
变式1.已知在直三棱柱中,,,为中点, 为中点,建立适当的空间直角坐标系,求向量, , 的坐标
解:建立如图所示的空间直角坐标系
设, ,
,
,
.
例题讲解
变式2.如图所示,垂直于正方形所在的平面,分别是的中点,并且.试建立适当的空间直角坐标系,求向量的坐标.
解:∵,平面,,
∴,,是两两垂直的单位向量.
∴如图建立空间直角坐标系,设,,
∵
∴.
例题讲解
练习1.如图一个正方体,若以为坐标原点,以棱,,所在的直线分别为轴、轴、轴,取正方体的棱长为单位长度,建立空间直角坐标系,则
①顶点, 的坐标分别为________________;
②棱中点的坐标为___________;
③正方形对角线的交点的坐标为___________;
④顶点关于轴对称的点的坐标为________________;
⑤顶点关于平面对称的点的坐标为________________;
⑥顶点关于点对称的点的坐标为________________.
i
j
O
k
x
y
z
A
B
C
D
C1
A1
B1
D1
(0,0,0),(0,1,1)
例题讲解
练习2.在空间直角坐标系中,点关于点的对称点的坐标是( )
. . . .
析:设所求对称点为,则点为线段的中点,
类比直角坐标系中的中点坐标公式可得
解得,
故选
小结
空间直角坐标系
空间直角坐标系
空间向量的坐标表示
空间向量基本定理
不共面,则对,唯一有序实数组,使得
点的坐标
向量的坐标
