沪科版八年级上册数学期中训练试题(含解析)
文档属性
| 名称 | 沪科版八年级上册数学期中训练试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 236.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 00:00:00 | ||
图片预览


文档简介
沪科版八年级上册数学期中训练试题
一、选择题。(每小题只有一个正确答案)
1.下面的四个点中,位于第一象限的点是( )
A.(1,-5) B.(1,5) C.(-1,5) D.(-1,-5)
2.若一个正比例函数的图象经过点(2,﹣3),则的值等于( )
A.-6 B.- C.- D.-
3.在△ABC中,若∠A=75°,∠B=50°,则∠C的度数为( )
A.35° B.45° C.50° D.55°
4.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为
A.(﹣1,0) B.(﹣1,﹣1) C.(﹣2,0) D.(﹣2,﹣1)
5.函数的自变量的取值范围是( )
A.≥-2 B.x>-2 C.x≠0 D.≥-2且≠0
6.如图,AE是△ABC的中线,D是BE上一点,若BE=5,DE=2,则CD的长为( )
A.7 B.6 C.5 D.4
7.(2015秋 萍乡期末)如果所示,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( )
①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AE平分∠BAC.
A.1 B.2 C.3 D.4
8.小军同学每天骑自行车上学,某天小军骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为( )
A.y=100t(15<t≤23) B.50t+650(15<t≤23)
C.y=100t-500(15<t≤23) D.y=100t+500(15<t≤23)
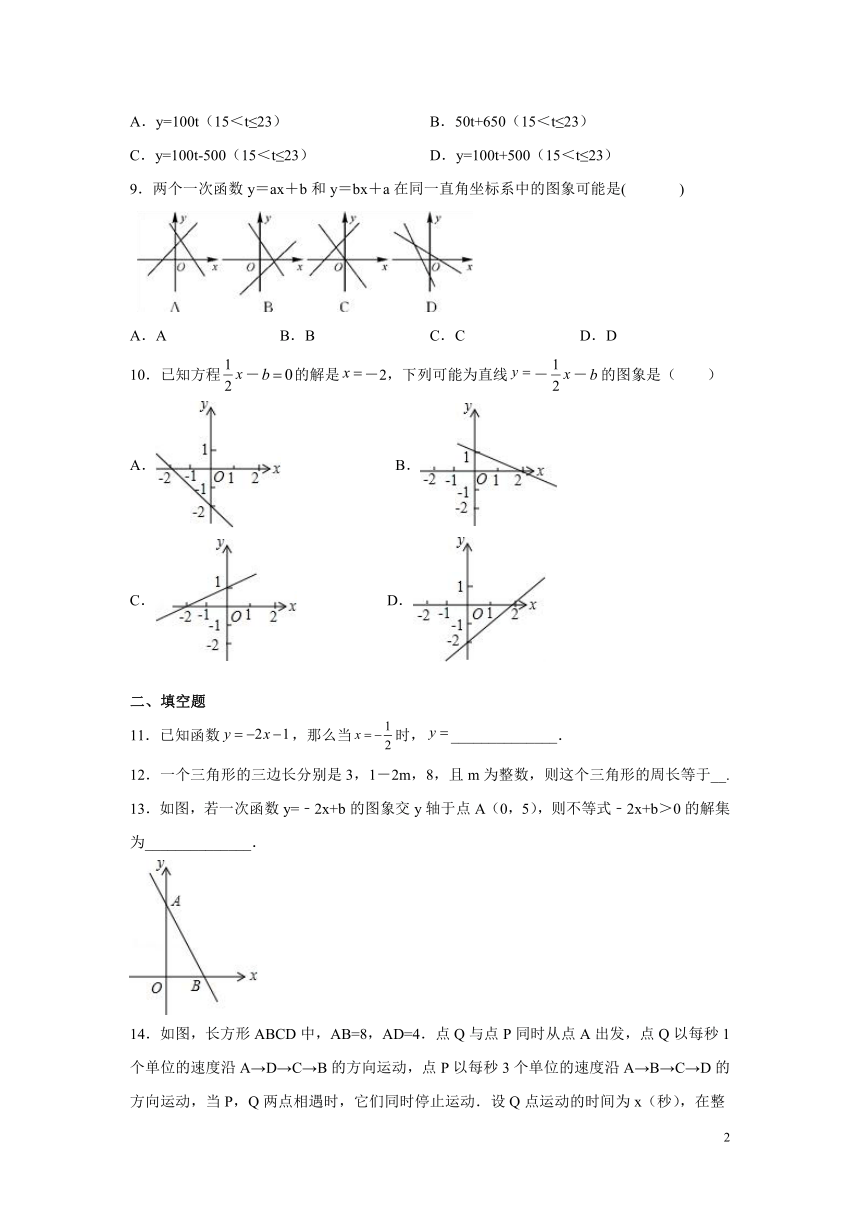
9.两个一次函数y=ax+b和y=bx+a在同一直角坐标系中的图象可能是( )
A.A B.B C.C D.D
10.已知方程-的解是-2,下列可能为直线--的图象是( )
A. B.
C. D.
二、填空题
11.已知函数,那么当时,______________.
12.一个三角形的三边长分别是3,1-2m,8,且m为整数,则这个三角形的周长等于__.
13.如图,若一次函数y=﹣2x+b的图象交y轴于点A(0,5),则不等式﹣2x+b>0的解集为______________.
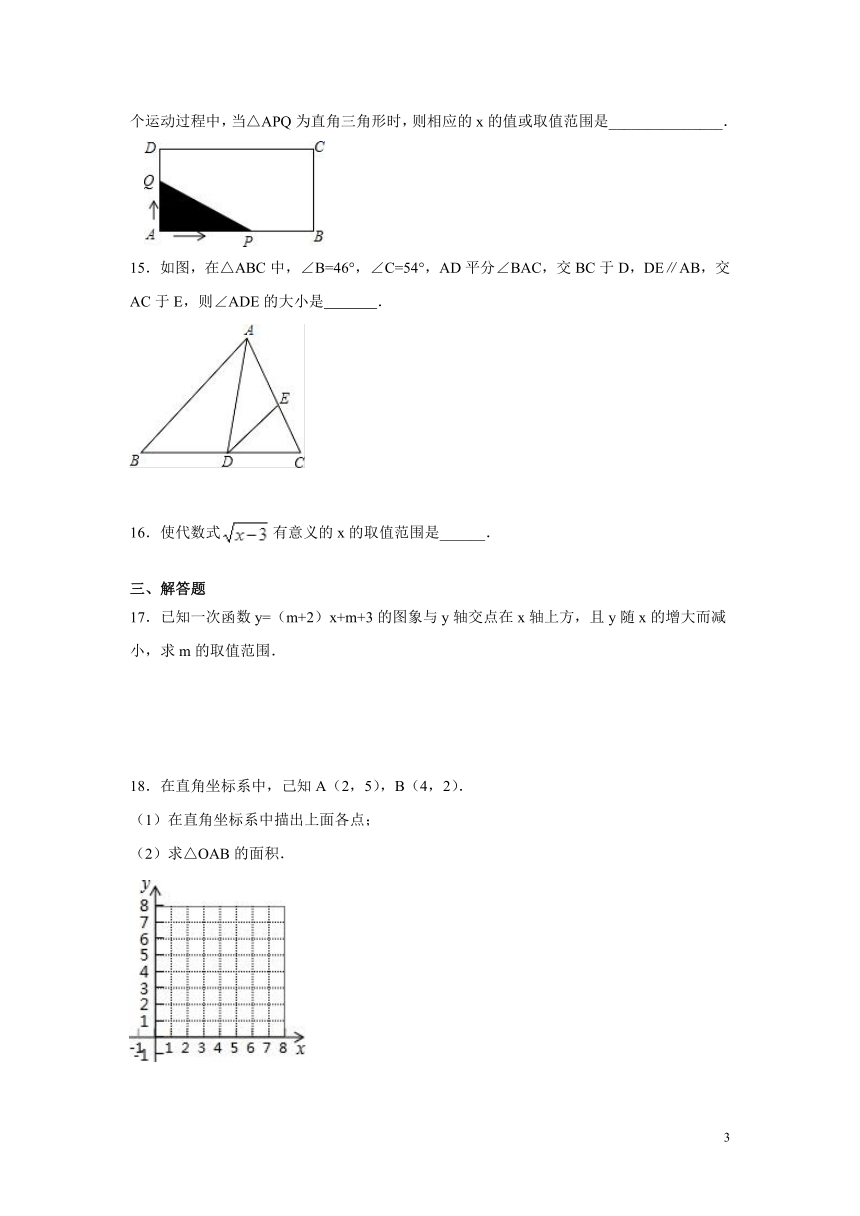
14.如图,长方形ABCD中,AB=8,AD=4.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是_______________.
15.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是 .
16.使代数式有意义的x的取值范围是______.
三、解答题
17.已知一次函数y=(m+2)x+m+3的图象与y轴交点在x轴上方,且y随x的增大而减小,求m的取值范围.
18.在直角坐标系中,己知A(2,5),B(4,2).
(1)在直角坐标系中描出上面各点;
(2)求△OAB的面积.
19.已知如图:在△ABC中,∠A=62°,∠ABD=∠DCE=36°,求∠BEC的度数.
20.如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.例如:由①②得③.
(1)你还能构造几个命题?请仿照上面的例子,将它们写出来.
(2)你构造的命题是真命题还是假命题?请选择一个加以证明.
21.如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠A=50°,求∠B的度数.
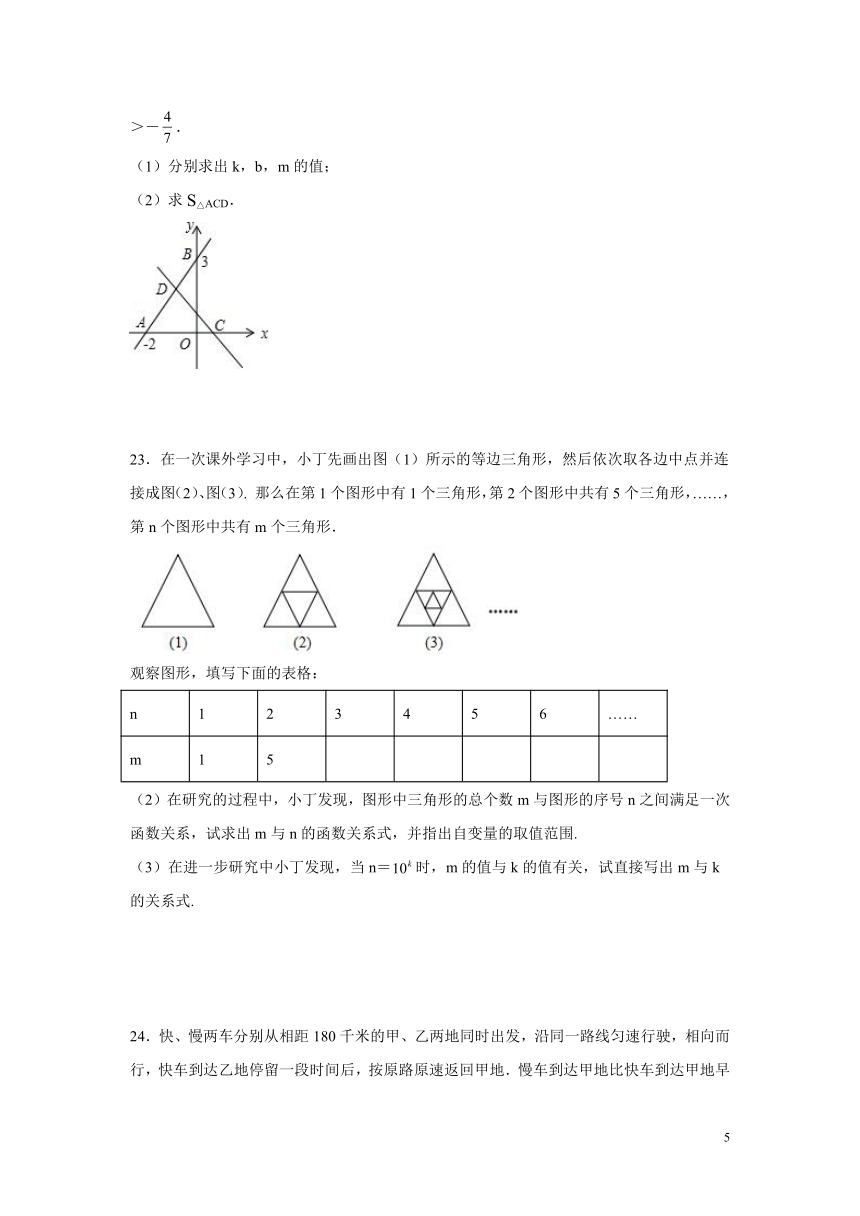
22.如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x>-.
(1)分别求出k,b,m的值;
(2)求S△ACD.
23.在一次课外学习中,小丁先画出图(1)所示的等边三角形,然后依次取各边中点并连接成图(2)、图(3). 那么在第1个图形中有1个三角形,第2个图形中共有5个三角形,……,第n个图形中共有m个三角形.
观察图形,填写下面的表格:
n 1 2 3 4 5 6 ……
m 1 5
(2)在研究的过程中,小丁发现,图形中三角形的总个数m与图形的序号n之间满足一次函数关系,试求出m与n的函数关系式,并指出自变量的取值范围.
(3)在进一步研究中小丁发现,当n=时,m的值与k的值有关,试直接写出m与k的关系式.
24.快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)求快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?直接写出答案.
25.某电话公司开设了两种手机通讯业务,甲种业务:使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;乙种业务:不交月租费,每通话1分钟,付话费0.6元(指市话).若一个月内通话x分钟,两种方式的费用分别为y1(元)和y2(元).
(1)分别求出y1、y2与x之间的函数关系式.
(2)根据每月可能的通话时间,作为消费者选用哪种缴费方式更实惠.
参考答案
1.B
【解析】
∵第一象限内的点P(a,b),其中a>0,b>0,
∴B选项的点(1,5)是第一象限内的点,
故选B.
2.C
【解析】
∵点(2,-3)在正比例函数上,
∴-3=2k,
∴k=-,
故选C.
3.D
【解析】
∵∠A+∠B+∠C=180o(三角形内角和为180 o),且∠A=75°,∠B=50°,
∴∠C=180 o-(∠A+∠B)=180 o-(75°+50°)=55°,
故选D.
4.B
【详解】
已知点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,根据向左平移横坐标减,向下平移纵坐标减的平移规律可得,点B的横坐标为1﹣2=﹣1,纵坐标为3﹣4=﹣1,所以B的坐标为(﹣1,﹣1).
故答案选B.
考点:坐标与图形变化﹣平移.
5.D
【解析】
∵要使有意义,
∴x+2≥0,x≠0,
∴x≥-2,x≠0,
故选D.
【点睛】分式有意义,分母不为0;二次根式的被开方数是非负数.
6.A
【解析】
∵AE是△ABC的中线,
∴BE=CE,
又∵BE=5,
∴CE=5,
又∵CD=CE+DE,DE=2,
∴CD=5+2=7,
故选A.
7.B
【分析】
根据角平分线的定义进行判断即可.
【详解】
解:AD不一定平分∠BAF,①错误;
AF不一定平分∠DAC,②错误;
∵∠1=∠2,∴AE平分∠DAF,③正确;
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠BAE=∠CAE,
∴AE平分∠BAC,④正确;
故选B.
【点睛】
三角形的角平分线、中线和高.
8.C
【解析】
∵用了8分钟骑行了剩余的800米,
∴速度v=米/分,
则可得y=1000+100(t-15)=100t-500(15<t≤23).
故选C.
9.B
【详解】
试题解析:A、对于y=ax+b,当a>0,图象经过第一、三象限,若b>0,则y=bx+a也要经过第一、三象限,所以A选项错误;
B、对于y=ax+b,当a>0,图象经过第一、三象限,若b<0,则y=bx+a经过第二、四象限,与y轴的交点在x轴上方,所以B选项正确;
C、对于y=ax+b,当a>0,图象经过第一、三象限,若b>0,则y=bx+a也要经过第一、三象限,所以C选项错误;
D、对于y=ax+b,当a<0,图象经过第二、四象限,若b>0,则y=bx+a经过第一、三象限,所以D选项错误.
故选B.
考点:一次函数的图象.
10.B
【解析】
∵方程-的解是-2,
∴直线y=-过点(-2,0),
∵系数k=〉0,
∴直线y=-经过第一、二、三象限,且与x轴相交于点(-2,0).
故选B.
【点睛】任何一元一次方程都可以转化为ax+b=0 (a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.
11.0
【解析】
把x= 代入y=-2x-1中,得
y=-2 =0.
故答案是:0.
12.18或20
【解析】
∵3,1﹣2m,8是角形的三边长,
∴8-3<1-2m<8+3,即5<1-2m<11,
∴-5又∵三边是整数,
∴m=-3或m=-4,
当m=-3时,1-2m=7,三角形的周长为:3+7+8=18;
当m=-4时,1-2m=9,三角形的周长为:3+9+8=20.
故答案是:20或18.
13.x<
【解析】
∵一次函数y=﹣2x+b的图象交y轴于点A(0,5),
∴b=5,
∴一次函数y=-2x+5,
∴-2x+5>0,
∴x<
故答案是:x<.
14.或
【解析】
当点P在AB上时,点Q在AD上时,此时△APQ为直角三角形,则0当点P在BC上时,点Q在AD上时,此时△APQ为锐角三角形,则当点P在C处,此时点Q在D处,此时△APQ为直角三角形,则x=4时;
当点P在CD上时,点Q在DC上时,此时△APQ为钝角三角形,则4故答案是:0【点睛】解答本题的关键是熟练掌握矩形的性质,还要熟练掌握三角形形状的判断,此题难度一般.
15.40°
【解析】
试题分析:根据DE∥AB可求得∠ADE=∠BAD,根据三角形内角和为180°和角平分线平分角的性质可求得∠BAD的值,即可解题. ∵DE∥AB, ∴∠ADE=∠BAD, ∵∠B=46°,∠C=54°,
∴∠BAD=180°﹣46°﹣54°=80°, ∵AD平分∠BAC, ∴∠BAD=40°, ∴∠ADE=40°
考点:(1)、三角形内角和定理;(2)、平行线的性质.
16.x≥3
【解析】
试题分析:二次根式的被开方数是非负数. 根据题意,得 x﹣3≥0, 解得,x≥3;
考点:二次根式有意义的条件.
17.-3<m<-2
【解析】
试题分析:由一次函数的象限的性质得出不等式,解不等式即可.
试题解析:
∵一次函数的图象与y轴交点在x轴上方,
∴2m+3>0,
∴m>
∵一次函数y随x的增大而减小,
∴m-2<0,
∴m<2.
综合上述可得:.
18.(1)见解析;(2)8
【解析】
试题分析:(1)描点,
(2)利用长方形面积减去三个直角三角形面积差求.
试题解析:
(1)如图所示:
(2)S△OAB=
=20-5-3-4
=8.
19.134°
【解析】
试题分析:先根据三角形内角和定理求出∠ADB的度数,再由补角的定义得出∠CDE的度数,根据三角形外角的性质即可得出结论.
试题解析:
∵△ABD中,∠A=62°,∠ABD=36°,
∴∠ADB=180°-62°-36°=82°,
∴∠CDE=180°-82°=98°.
∵∠BEC是△CDE的外角,∠DCE=36°,
∴∠BCE=∠CDE+∠DCE=98°+36°=134°.
20.见解析
【解析】
试题分析:(1)分别以其中2句话为条件,第三句话为结论可写出3个命题;
(2)根据平行线的判定与性质对3个命题分别进行证明,判断它们的真假.
试题解析:
(1)由①②得到③;由①③得到②;由②③得到①;
(2)∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
所以由①②得到③为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
所以由①③得到②为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
所以由②③得到①为真命题.
【点睛】判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
21.70°
【解析】
试题分析:根据三角形内角和定理,在△CDE中,求得∠EDC的度数,由三角形外角的性质得到∠ACD的度数,再由角平分线的性质求得∠BCA的度数,再由三角形内角和定理求得∠B的度数.
试题解析:
∵CE是AB边上的高,
∴∠CED=90o
又∵∠CED+∠ECD+∠EDC=180 o ,∠DCE=10°,
∴∠EDC=80 o
又∵∠EDC=∠A+∠DCA,∠A=50°,
∴∠DCA=30 o
又∵CD是∠ACB的角平分线
∴∠BCA=2∠ACD=60 o
又∵∠A+∠B+∠BCA=180 o
∴∠B=(180-60-50)o =70 o.
22.(1)k=,b=3,m=2;(2)
【解析】
试题分析:(1)将A、B两点坐标代入y=kx+b中,即可求得k、b的值;再由不等式kx+b>1﹣mx的解集是x>-求得m的值;
(2)求得C点坐标,由S△ACD= 求解.
试题解析:
(1)∵直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3),
,
解得:k=,b=3,
∵关于x的不等式kx+b>1﹣mx的解集是x>-,∴点D的横坐标为-,
将x=-代入y=x+3,得:y=,
将x=-,y=代入y=1﹣mx,
解得:m=2;
(2)对于y=1﹣2x,令y=0,得:x=,∴点C的坐标为(,0),
∴S△ACD=×[﹣(﹣2)]×=.
23.(1)9,13,17;(2)(n>0,且n为整数);(3)(k>0,且k为整数)
【解析】
试题分析:(1)由后一个图形三角形的个数总是在前一个图形的前面加4的规律直接写出三角形的个数;(2)用待定系数法求m、n的关系式;(3)由关系式直接写出即可.
试题解析:
(1)9,13,17;
设m=kn+b,将(1,1)和(2,5)代入,得:
,
解得:
∴(n>0,且n为整数)
(3)(k>0,且k为整数)
24.(1)120千米/时,60千米/时(2)y=﹣120x+420(2≤x≤);(3)两车出发后经过或或小时相距90千米的路程
【解析】
试题分析:(1)根据路程与相应的时间,求得慢车的速度,再根据慢车速度是快车速度的一半,求得快车速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:
(1)快车速度:180×2÷()=120千米/时,
慢车速度:120÷2=60千米/时;
(2)快车停留的时间:﹣×2=(小时),
+=2(小时),即C(2,180),
设CD的解析式为:y=kx+b,则
将C(2,180),D(,0)代入,得
,
解得,
∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤);
(3)相遇之前:120x+60x+90=180,
解得x=;
相遇之后:120x+60x﹣90=180,
解得x=;
快车从甲地到乙地需要180÷120=小时,
快车返回之后:60x=90+120(x﹣﹣)
解得x=
综上所述,两车出发后经过或或小时相距90千米的路程.
【点睛】解决问题的关键是掌握待定系数法求一次函数解析式.求一次函数y=kx+b,需要两组x,y的值或图象上两个点的坐标.在解题时注意分类思想的运用.
25.(1)、y1=50+0.4x,y2=0.6x;(2)、当通话时间小于250分钟时,选择乙种通信业务更优惠;当通话时间等于250分钟时,选择两种通信业务一样;当通话时间大于250分钟时,选择甲种通信业务更优惠.
【分析】
(1)根据两种费用的缴费方式分别列式计算即可得解;
(2)先写出两种缴费方式的函数关系式,再分情况列出不等式然后求解即可.
【详解】
解: (1)由题意可知:y1=50+0.4x,y2=0.6x;
(2)y1=50+0.4x,y2=0.6x, 当y1>y2即50+0.4x>0.6x时,x<250,
当y1=y2即50+0.4x=0.6x时,x=250,
当y1<y2即50+0.4x<0.6x时,x>250,
所以,当通话时间小于250分钟时,选择乙种通信业务更优惠, 当通话时间等于250分钟时,选择两种通信业务一样, 当通话时间大于250分钟时,选择甲种通信业务更优惠.
考点:一次函数的应用.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案)
1.下面的四个点中,位于第一象限的点是( )
A.(1,-5) B.(1,5) C.(-1,5) D.(-1,-5)
2.若一个正比例函数的图象经过点(2,﹣3),则的值等于( )
A.-6 B.- C.- D.-
3.在△ABC中,若∠A=75°,∠B=50°,则∠C的度数为( )
A.35° B.45° C.50° D.55°
4.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为
A.(﹣1,0) B.(﹣1,﹣1) C.(﹣2,0) D.(﹣2,﹣1)
5.函数的自变量的取值范围是( )
A.≥-2 B.x>-2 C.x≠0 D.≥-2且≠0
6.如图,AE是△ABC的中线,D是BE上一点,若BE=5,DE=2,则CD的长为( )
A.7 B.6 C.5 D.4
7.(2015秋 萍乡期末)如果所示,已知∠1=∠2,∠3=∠4,则下列结论正确的个数为( )
①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AE平分∠BAC.
A.1 B.2 C.3 D.4
8.小军同学每天骑自行车上学,某天小军骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为( )
A.y=100t(15<t≤23) B.50t+650(15<t≤23)
C.y=100t-500(15<t≤23) D.y=100t+500(15<t≤23)
9.两个一次函数y=ax+b和y=bx+a在同一直角坐标系中的图象可能是( )
A.A B.B C.C D.D
10.已知方程-的解是-2,下列可能为直线--的图象是( )
A. B.
C. D.
二、填空题
11.已知函数,那么当时,______________.
12.一个三角形的三边长分别是3,1-2m,8,且m为整数,则这个三角形的周长等于__.
13.如图,若一次函数y=﹣2x+b的图象交y轴于点A(0,5),则不等式﹣2x+b>0的解集为______________.
14.如图,长方形ABCD中,AB=8,AD=4.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是_______________.
15.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是 .
16.使代数式有意义的x的取值范围是______.
三、解答题
17.已知一次函数y=(m+2)x+m+3的图象与y轴交点在x轴上方,且y随x的增大而减小,求m的取值范围.
18.在直角坐标系中,己知A(2,5),B(4,2).
(1)在直角坐标系中描出上面各点;
(2)求△OAB的面积.
19.已知如图:在△ABC中,∠A=62°,∠ABD=∠DCE=36°,求∠BEC的度数.
20.如图,现有以下3句话:①AB∥CD,②∠B=∠C.③∠E=∠F.请以其中2句话为条件,第三句话为结论构造命题.例如:由①②得③.
(1)你还能构造几个命题?请仿照上面的例子,将它们写出来.
(2)你构造的命题是真命题还是假命题?请选择一个加以证明.
21.如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠A=50°,求∠B的度数.
22.如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x>-.
(1)分别求出k,b,m的值;
(2)求S△ACD.
23.在一次课外学习中,小丁先画出图(1)所示的等边三角形,然后依次取各边中点并连接成图(2)、图(3). 那么在第1个图形中有1个三角形,第2个图形中共有5个三角形,……,第n个图形中共有m个三角形.
观察图形,填写下面的表格:
n 1 2 3 4 5 6 ……
m 1 5
(2)在研究的过程中,小丁发现,图形中三角形的总个数m与图形的序号n之间满足一次函数关系,试求出m与n的函数关系式,并指出自变量的取值范围.
(3)在进一步研究中小丁发现,当n=时,m的值与k的值有关,试直接写出m与k的关系式.
24.快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)求快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?直接写出答案.
25.某电话公司开设了两种手机通讯业务,甲种业务:使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;乙种业务:不交月租费,每通话1分钟,付话费0.6元(指市话).若一个月内通话x分钟,两种方式的费用分别为y1(元)和y2(元).
(1)分别求出y1、y2与x之间的函数关系式.
(2)根据每月可能的通话时间,作为消费者选用哪种缴费方式更实惠.
参考答案
1.B
【解析】
∵第一象限内的点P(a,b),其中a>0,b>0,
∴B选项的点(1,5)是第一象限内的点,
故选B.
2.C
【解析】
∵点(2,-3)在正比例函数上,
∴-3=2k,
∴k=-,
故选C.
3.D
【解析】
∵∠A+∠B+∠C=180o(三角形内角和为180 o),且∠A=75°,∠B=50°,
∴∠C=180 o-(∠A+∠B)=180 o-(75°+50°)=55°,
故选D.
4.B
【详解】
已知点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,根据向左平移横坐标减,向下平移纵坐标减的平移规律可得,点B的横坐标为1﹣2=﹣1,纵坐标为3﹣4=﹣1,所以B的坐标为(﹣1,﹣1).
故答案选B.
考点:坐标与图形变化﹣平移.
5.D
【解析】
∵要使有意义,
∴x+2≥0,x≠0,
∴x≥-2,x≠0,
故选D.
【点睛】分式有意义,分母不为0;二次根式的被开方数是非负数.
6.A
【解析】
∵AE是△ABC的中线,
∴BE=CE,
又∵BE=5,
∴CE=5,
又∵CD=CE+DE,DE=2,
∴CD=5+2=7,
故选A.
7.B
【分析】
根据角平分线的定义进行判断即可.
【详解】
解:AD不一定平分∠BAF,①错误;
AF不一定平分∠DAC,②错误;
∵∠1=∠2,∴AE平分∠DAF,③正确;
∵∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠BAE=∠CAE,
∴AE平分∠BAC,④正确;
故选B.
【点睛】
三角形的角平分线、中线和高.
8.C
【解析】
∵用了8分钟骑行了剩余的800米,
∴速度v=米/分,
则可得y=1000+100(t-15)=100t-500(15<t≤23).
故选C.
9.B
【详解】
试题解析:A、对于y=ax+b,当a>0,图象经过第一、三象限,若b>0,则y=bx+a也要经过第一、三象限,所以A选项错误;
B、对于y=ax+b,当a>0,图象经过第一、三象限,若b<0,则y=bx+a经过第二、四象限,与y轴的交点在x轴上方,所以B选项正确;
C、对于y=ax+b,当a>0,图象经过第一、三象限,若b>0,则y=bx+a也要经过第一、三象限,所以C选项错误;
D、对于y=ax+b,当a<0,图象经过第二、四象限,若b>0,则y=bx+a经过第一、三象限,所以D选项错误.
故选B.
考点:一次函数的图象.
10.B
【解析】
∵方程-的解是-2,
∴直线y=-过点(-2,0),
∵系数k=〉0,
∴直线y=-经过第一、二、三象限,且与x轴相交于点(-2,0).
故选B.
【点睛】任何一元一次方程都可以转化为ax+b=0 (a,b为常数,a≠0)的形式,所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值.
11.0
【解析】
把x= 代入y=-2x-1中,得
y=-2 =0.
故答案是:0.
12.18或20
【解析】
∵3,1﹣2m,8是角形的三边长,
∴8-3<1-2m<8+3,即5<1-2m<11,
∴-5
∴m=-3或m=-4,
当m=-3时,1-2m=7,三角形的周长为:3+7+8=18;
当m=-4时,1-2m=9,三角形的周长为:3+9+8=20.
故答案是:20或18.
13.x<
【解析】
∵一次函数y=﹣2x+b的图象交y轴于点A(0,5),
∴b=5,
∴一次函数y=-2x+5,
∴-2x+5>0,
∴x<
故答案是:x<.
14.或
【解析】
当点P在AB上时,点Q在AD上时,此时△APQ为直角三角形,则0
当点P在CD上时,点Q在DC上时,此时△APQ为钝角三角形,则4
15.40°
【解析】
试题分析:根据DE∥AB可求得∠ADE=∠BAD,根据三角形内角和为180°和角平分线平分角的性质可求得∠BAD的值,即可解题. ∵DE∥AB, ∴∠ADE=∠BAD, ∵∠B=46°,∠C=54°,
∴∠BAD=180°﹣46°﹣54°=80°, ∵AD平分∠BAC, ∴∠BAD=40°, ∴∠ADE=40°
考点:(1)、三角形内角和定理;(2)、平行线的性质.
16.x≥3
【解析】
试题分析:二次根式的被开方数是非负数. 根据题意,得 x﹣3≥0, 解得,x≥3;
考点:二次根式有意义的条件.
17.-3<m<-2
【解析】
试题分析:由一次函数的象限的性质得出不等式,解不等式即可.
试题解析:
∵一次函数的图象与y轴交点在x轴上方,
∴2m+3>0,
∴m>
∵一次函数y随x的增大而减小,
∴m-2<0,
∴m<2.
综合上述可得:.
18.(1)见解析;(2)8
【解析】
试题分析:(1)描点,
(2)利用长方形面积减去三个直角三角形面积差求.
试题解析:
(1)如图所示:
(2)S△OAB=
=20-5-3-4
=8.
19.134°
【解析】
试题分析:先根据三角形内角和定理求出∠ADB的度数,再由补角的定义得出∠CDE的度数,根据三角形外角的性质即可得出结论.
试题解析:
∵△ABD中,∠A=62°,∠ABD=36°,
∴∠ADB=180°-62°-36°=82°,
∴∠CDE=180°-82°=98°.
∵∠BEC是△CDE的外角,∠DCE=36°,
∴∠BCE=∠CDE+∠DCE=98°+36°=134°.
20.见解析
【解析】
试题分析:(1)分别以其中2句话为条件,第三句话为结论可写出3个命题;
(2)根据平行线的判定与性质对3个命题分别进行证明,判断它们的真假.
试题解析:
(1)由①②得到③;由①③得到②;由②③得到①;
(2)∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
所以由①②得到③为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
所以由①③得到②为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
所以由②③得到①为真命题.
【点睛】判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
21.70°
【解析】
试题分析:根据三角形内角和定理,在△CDE中,求得∠EDC的度数,由三角形外角的性质得到∠ACD的度数,再由角平分线的性质求得∠BCA的度数,再由三角形内角和定理求得∠B的度数.
试题解析:
∵CE是AB边上的高,
∴∠CED=90o
又∵∠CED+∠ECD+∠EDC=180 o ,∠DCE=10°,
∴∠EDC=80 o
又∵∠EDC=∠A+∠DCA,∠A=50°,
∴∠DCA=30 o
又∵CD是∠ACB的角平分线
∴∠BCA=2∠ACD=60 o
又∵∠A+∠B+∠BCA=180 o
∴∠B=(180-60-50)o =70 o.
22.(1)k=,b=3,m=2;(2)
【解析】
试题分析:(1)将A、B两点坐标代入y=kx+b中,即可求得k、b的值;再由不等式kx+b>1﹣mx的解集是x>-求得m的值;
(2)求得C点坐标,由S△ACD= 求解.
试题解析:
(1)∵直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3),
,
解得:k=,b=3,
∵关于x的不等式kx+b>1﹣mx的解集是x>-,∴点D的横坐标为-,
将x=-代入y=x+3,得:y=,
将x=-,y=代入y=1﹣mx,
解得:m=2;
(2)对于y=1﹣2x,令y=0,得:x=,∴点C的坐标为(,0),
∴S△ACD=×[﹣(﹣2)]×=.
23.(1)9,13,17;(2)(n>0,且n为整数);(3)(k>0,且k为整数)
【解析】
试题分析:(1)由后一个图形三角形的个数总是在前一个图形的前面加4的规律直接写出三角形的个数;(2)用待定系数法求m、n的关系式;(3)由关系式直接写出即可.
试题解析:
(1)9,13,17;
设m=kn+b,将(1,1)和(2,5)代入,得:
,
解得:
∴(n>0,且n为整数)
(3)(k>0,且k为整数)
24.(1)120千米/时,60千米/时(2)y=﹣120x+420(2≤x≤);(3)两车出发后经过或或小时相距90千米的路程
【解析】
试题分析:(1)根据路程与相应的时间,求得慢车的速度,再根据慢车速度是快车速度的一半,求得快车速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:
(1)快车速度:180×2÷()=120千米/时,
慢车速度:120÷2=60千米/时;
(2)快车停留的时间:﹣×2=(小时),
+=2(小时),即C(2,180),
设CD的解析式为:y=kx+b,则
将C(2,180),D(,0)代入,得
,
解得,
∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤);
(3)相遇之前:120x+60x+90=180,
解得x=;
相遇之后:120x+60x﹣90=180,
解得x=;
快车从甲地到乙地需要180÷120=小时,
快车返回之后:60x=90+120(x﹣﹣)
解得x=
综上所述,两车出发后经过或或小时相距90千米的路程.
【点睛】解决问题的关键是掌握待定系数法求一次函数解析式.求一次函数y=kx+b,需要两组x,y的值或图象上两个点的坐标.在解题时注意分类思想的运用.
25.(1)、y1=50+0.4x,y2=0.6x;(2)、当通话时间小于250分钟时,选择乙种通信业务更优惠;当通话时间等于250分钟时,选择两种通信业务一样;当通话时间大于250分钟时,选择甲种通信业务更优惠.
【分析】
(1)根据两种费用的缴费方式分别列式计算即可得解;
(2)先写出两种缴费方式的函数关系式,再分情况列出不等式然后求解即可.
【详解】
解: (1)由题意可知:y1=50+0.4x,y2=0.6x;
(2)y1=50+0.4x,y2=0.6x, 当y1>y2即50+0.4x>0.6x时,x<250,
当y1=y2即50+0.4x=0.6x时,x=250,
当y1<y2即50+0.4x<0.6x时,x>250,
所以,当通话时间小于250分钟时,选择乙种通信业务更优惠, 当通话时间等于250分钟时,选择两种通信业务一样, 当通话时间大于250分钟时,选择甲种通信业务更优惠.
考点:一次函数的应用.
(
2
)
(
1
)
同课章节目录
