22.3实际问题与二次函数(第3课时拱桥问题)同步课件(共14张PPT) 2023-2024学年九年级数学上册(人教版)
文档属性
| 名称 | 22.3实际问题与二次函数(第3课时拱桥问题)同步课件(共14张PPT) 2023-2024学年九年级数学上册(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
人教版数学九年级上册
第22.3 实际问题与二次函数
(第3课时拱桥问题)
学习目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
3.能运用二次函数的图象与性质进行决策.
复习引入
1.函数y=ax2(a≠0)的图象是一条_______,它的顶点坐标是_______,对称轴是_____,当a____时,开口向上,当a____时,开口向下.
2.二次函数解析式的形式有:
①一般式:____________,
②顶点式:_____________,
③交点式:________________.
3.(1)如图所示的抛物线,可以根据顶点所在的位置设为_________,也可以根据抛物线与x轴的交点坐标设为______________.
(2)由A,B两点的横坐标,可以求得线段AB的长
为______.
抛物线
(0,0)
y轴
>0
<0
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
y=ax2+2
y=a(x+2)(x-2)
4
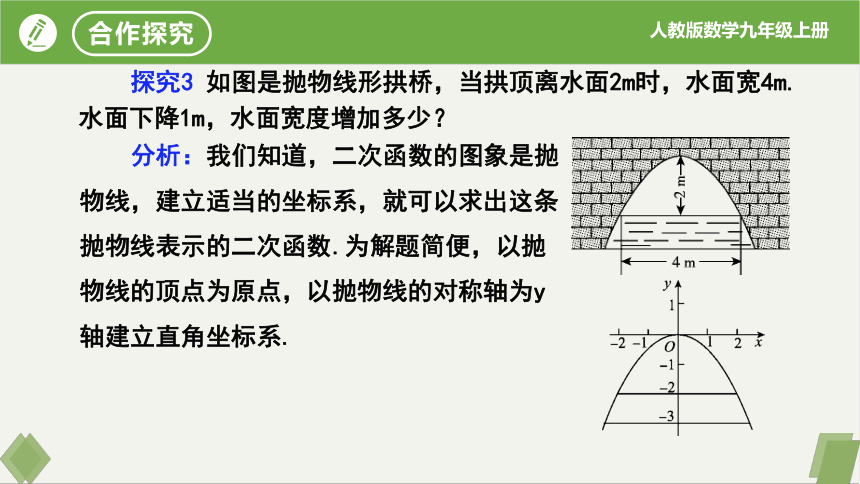
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
探究3 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
合作探究
合作探究
探究3 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
解:设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得
-2=a×22,解得,a=-
∴ 这条抛物线表示的二次函数为:y=-x2
当水面下降1m时,水面的纵坐标为-3.
当y=-3时,x=±.
∴当水面下降1m时,水面的宽度为2m.
∴水面的宽度增加了(2-4)m.
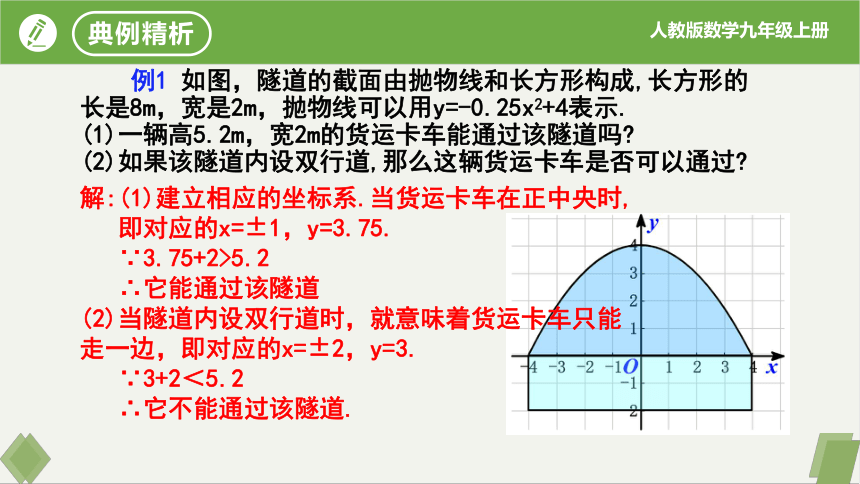
例1 如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-0.25x2+4表示.
(1)一辆高5.2m,宽2m的货运卡车能通过该隧道吗
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过
解:(1)建立相应的坐标系.当货运卡车在正中央时,
即对应的x=±1,y=3.75.
∵3.75+2>5.2
∴它能通过该隧道
(2)当隧道内设双行道时,就意味着货运卡车只能走一边,即对应的x=±2,y=3.
∵3+2<5.2
∴它不能通过该隧道.
典例精析
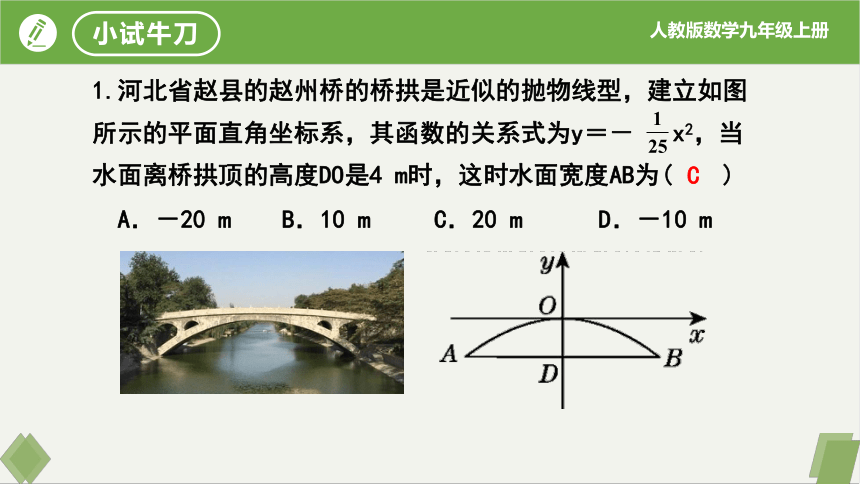
1.河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如图所示的平面直角坐标系,其函数的关系式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m
C
小试牛刀
1.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.5米 C.6米 D.7米
2.向上发射一枚炮弹,经x秒后的高度为y米,且时间与高度关系为y=ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9.5秒 B.第10秒 C.第10.5秒 D.第11秒
A
C
课堂检测
3.如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米
解:如图,建立直角坐标系
则点B的坐标是(0,3.5),点C的坐标是
(1.5,3.05)
点A表示运动员投篮球的出手处
设y=ax2+3.5
把C(1.5,3.05)代入y=ax2+3.5得
3.05=2.25a+3.5,解得a=-0.2
∴y=-0.2x2+3.5
当x=-2.5时,y=2.25
故运动员出手时的高度为2.25m。
课堂检测
1.如图,隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=- x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3 m,到地面OA的距离为172 m.
(1)求该抛物线对应的函数解析式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货运汽车能否安全通过?
拓展训练
解:(1)根据题意得B(0,4),C(3, ). 把点B(0,4),C(3, )的
坐标分别代入y=-16x2+bx+c,
所以抛物线对应的函数解析式为y=-16x2+2x+4,
即y=-16(x-6)2+10.
所以D点的坐标为(6,10).
所以拱顶D到地面OA的距离为10 m.
得
解得
拓展训练
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货运汽车能否安全通过?
由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
所以这辆货运汽车能安全通过.
拓展训练
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在____s后落地.
2.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是____米.
4
4
课后作业
谢谢聆听
人教版数学九年级上册
第22.3 实际问题与二次函数
(第3课时拱桥问题)
学习目标
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
3.能运用二次函数的图象与性质进行决策.
复习引入
1.函数y=ax2(a≠0)的图象是一条_______,它的顶点坐标是_______,对称轴是_____,当a____时,开口向上,当a____时,开口向下.
2.二次函数解析式的形式有:
①一般式:____________,
②顶点式:_____________,
③交点式:________________.
3.(1)如图所示的抛物线,可以根据顶点所在的位置设为_________,也可以根据抛物线与x轴的交点坐标设为______________.
(2)由A,B两点的横坐标,可以求得线段AB的长
为______.
抛物线
(0,0)
y轴
>0
<0
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
y=ax2+2
y=a(x+2)(x-2)
4
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.为解题简便,以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
探究3 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
合作探究
合作探究
探究3 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
解:设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得
-2=a×22,解得,a=-
∴ 这条抛物线表示的二次函数为:y=-x2
当水面下降1m时,水面的纵坐标为-3.
当y=-3时,x=±.
∴当水面下降1m时,水面的宽度为2m.
∴水面的宽度增加了(2-4)m.
例1 如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线可以用y=-0.25x2+4表示.
(1)一辆高5.2m,宽2m的货运卡车能通过该隧道吗
(2)如果该隧道内设双行道,那么这辆货运卡车是否可以通过
解:(1)建立相应的坐标系.当货运卡车在正中央时,
即对应的x=±1,y=3.75.
∵3.75+2>5.2
∴它能通过该隧道
(2)当隧道内设双行道时,就意味着货运卡车只能走一边,即对应的x=±2,y=3.
∵3+2<5.2
∴它不能通过该隧道.
典例精析
1.河北省赵县的赵州桥的桥拱是近似的抛物线型,建立如图所示的平面直角坐标系,其函数的关系式为y=- x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为( )
A.-20 m B.10 m C.20 m D.-10 m
C
小试牛刀
1.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.5米 C.6米 D.7米
2.向上发射一枚炮弹,经x秒后的高度为y米,且时间与高度关系为y=ax2+bx.若此炮弹在第7秒与第14秒时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9.5秒 B.第10秒 C.第10.5秒 D.第11秒
A
C
课堂检测
3.如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米
解:如图,建立直角坐标系
则点B的坐标是(0,3.5),点C的坐标是
(1.5,3.05)
点A表示运动员投篮球的出手处
设y=ax2+3.5
把C(1.5,3.05)代入y=ax2+3.5得
3.05=2.25a+3.5,解得a=-0.2
∴y=-0.2x2+3.5
当x=-2.5时,y=2.25
故运动员出手时的高度为2.25m。
课堂检测
1.如图,隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=- x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3 m,到地面OA的距离为172 m.
(1)求该抛物线对应的函数解析式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货运汽车能否安全通过?
拓展训练
解:(1)根据题意得B(0,4),C(3, ). 把点B(0,4),C(3, )的
坐标分别代入y=-16x2+bx+c,
所以抛物线对应的函数解析式为y=-16x2+2x+4,
即y=-16(x-6)2+10.
所以D点的坐标为(6,10).
所以拱顶D到地面OA的距离为10 m.
得
解得
拓展训练
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货运汽车能否安全通过?
由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
所以这辆货运汽车能安全通过.
拓展训练
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在____s后落地.
2.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是____米.
4
4
课后作业
谢谢聆听
同课章节目录
