北师大高中数学选择性必修第一册第四章量课时作业32数学建模活动(三) (含解析)
文档属性
| 名称 | 北师大高中数学选择性必修第一册第四章量课时作业32数学建模活动(三) (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 801.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 00:00:00 | ||
图片预览




文档简介
北师大高中数学选择性必修第一册
第四章量课时作业32数学建模活动(三)(原卷版)
一、选择题
1. 若矩形ABCD的一边长为x,周长为20,则当矩形面积最大时,x= ( C )
A.3 B.4
C.5 D.16
2. 某食品加工厂2021年获利20万元,经调整食品结构,开发新产品. 计划从2022年开始每年比上一年获利增加20%,问从哪一年开始这家加工厂年获利超过60万元(已知lg 2≈0. 301 0,lg 3≈0. 477 1). ( C )
A.2026年 B.2027年
C.2028年 D.2029年
3. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系:
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p,则x,p分别为 ( B )
A.35,225 B.40,300
C.45,350 D.45,400
4. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费. 某职工某月缴水费16m元,则该职工这个月实际用水为 ( A )
A.13立方米 B.14立方米
C.18立方米 D.26立方米
5. 已知光通过一块某种玻璃,强度要损失10%. 那么要使光的强度减弱到原来的以下,则至少需要通过这样的玻璃(参考数据:lg 3≈0. 477 1,lg 2≈0. 301 0) ( B )
A.6块 B.7块 C.8块 D.9块
6. 2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5 000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除:(3)专项附加扣除包括①赡养老人费用,②子女教育费用,③继续教育费用,④大病医疗费用等. 其中前两项的扣除标准为①赡养老人费用:每月扣除2 000元,②子女教育费用:每个子女每月扣除1 000元.
新的个税政策的税率表部分内容如下:
级数 一级 二级 三级 …
每月应纳税所得额x元(含税) x≤3 000 3 000<x≤12 000 12 000<x≤25 000 …
税率(%) 3 10 20 …
现有李某月收入为19 000元,膝下有一名子女,需赡养老人(除此之外无其他专项附加扣除),则他该月应交纳的个税金额为 ( B )
A.570 B.890
C.1 100 D.1 900
7. 某游轮在A处看灯塔B在A的北偏东75°方向上,距离为12海里,灯塔C在A的北偏西30°方向上,距离为8海里. 游轮由A向正北方向航行到D处时,再看灯塔B在D的南偏东60°方向上,则C与D的距离为 ( B )
A.20海里 B.8海里
C.23海里 D.24海里
8. (多选题)如下图, △OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t<2)左侧的图形的面积为f(t),现给出函数f(t)的四个性质,其中说法正确的是 ( BD )
A.f
B.f(t)在(0,2)上单调递增
C.当t=1时,f(t)取得最大值
D.对于任意的t∈(0,2),都有f(t)+f(2-t)=
二、填空题
9. 某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2. 718…自然对数的底数,k,b为常数),若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是24 小时.
10. 某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0. 01%,若初始时含杂质0. 2%,每次过滤可使杂质含量减少三分之一,则应过滤8 次才能使得这种液体达到要求. (已知lg 2≈0. 301 0,lg 3≈0. 477 1)
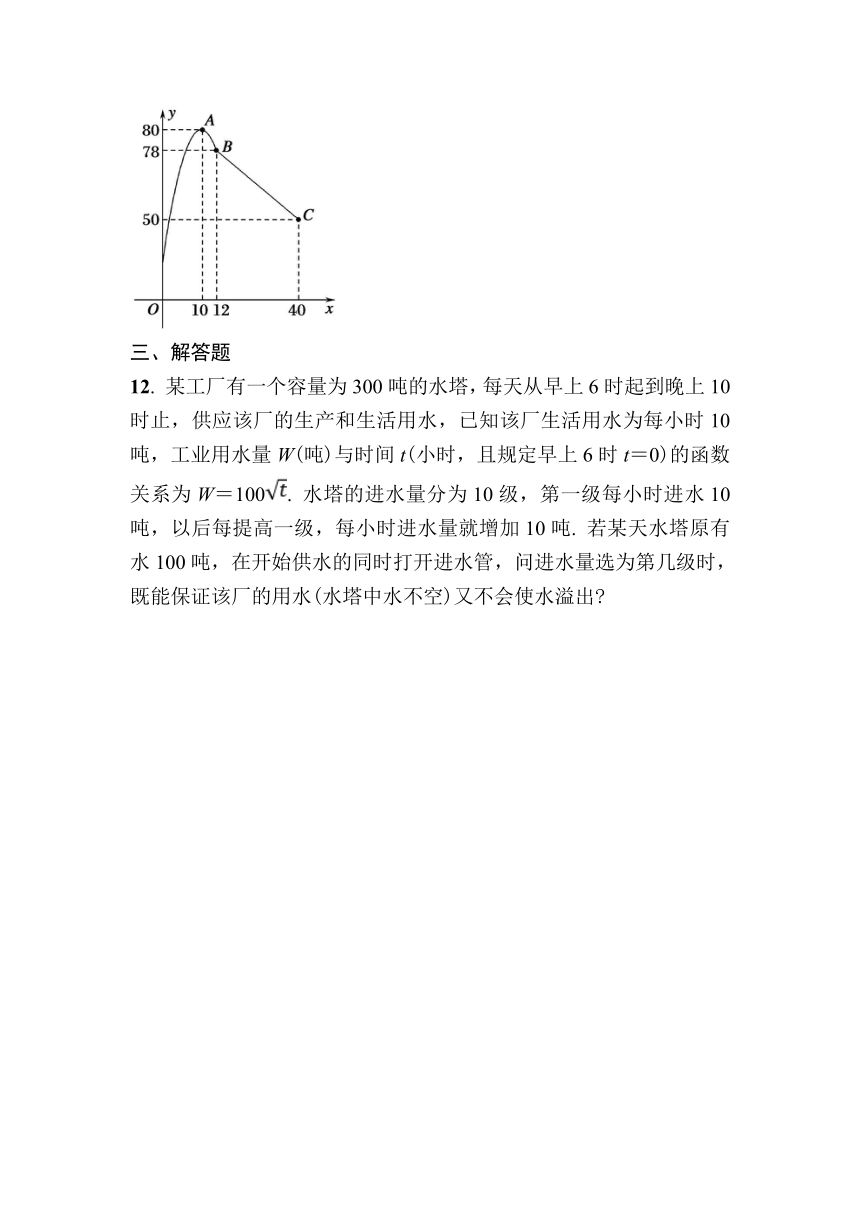
11. 学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50). 根据专家研究,当注意力指数大于62时,学习效果最佳. 要使得学生学习效果最佳,则教师安排核心内容的时间段为(4,28). (写成区间形式)
三、解答题
12. 某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止,供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100. 水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨. 若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出
13. 某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 1~50 51~100 100以上
门票价格 13元/人 11元/人 9元/人
两个旅游团队计划游览该景点. 若分别购票,则共需支付门票费1 290元;若合并成一个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为 ( B )
A.20 B.30 C.35 D.40
14. 近年来,我国在航天领域取得了巨大成就,得益于我国先进的运载火箭技术. 据了解,在不考虑空气阻力和地球引力的理想状态下,可以用公式v=v0ln计算火箭的最大速度v m/s,其中v0 m/s是喷流相对速度,m kg是火箭(除推进剂外)的质量,M kg是推进剂与火箭质量的总和,称为“总质比”. 已知A型火箭的喷流相对速度为2 000 m/s. 经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的1. 5倍,总质比变为原来的,若要使火箭的最大速度至少增加800 m/s,则在材料更新和技术改进前总质比的最小整数值为279. (参考数据:ln 330≈5. 8,2. 225<e0. 8<2. 226).
15. 某企业参加A项目生产的工人为1 000人,平均每人每年创造利润10万元. 根据现实的需要,从A项目中调出x人参与B项目的售后服务工作,每人每年可以创造利润10万元(a>0),A项目余下的工人每人每年创造利润将提高0. 2x%.
(1)若要保证A项目余下的工人创造的年总利润不低于原来1 000名工人创造的年总利润,则最多调出多少人参加B项目从事售后服务工作
(2)在(1)的条件下,当从A项目调出的人数不能超过总人数的40%时,才能使得A项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数a的取值范围.
北师大高中数学选择性必修第一册
第四章量课时作业32数学建模活动(三)(解析版)
一、选择题
1. 若矩形ABCD的一边长为x,周长为20,则当矩形面积最大时,x= ( C )
A.3 B.4
C.5 D.16
解析:矩形另一边长为=10-x,且有0<x<10,面积为f(x)=x(10-x)=-(x-5)2+25,所以,当x=5时,y=f(x)取最大值. 故选C.
2. 某食品加工厂2021年获利20万元,经调整食品结构,开发新产品. 计划从2022年开始每年比上一年获利增加20%,问从哪一年开始这家加工厂年获利超过60万元(已知lg 2≈0. 301 0,lg 3≈0. 477 1). ( C )
A.2026年 B.2027年
C.2028年 D.2029年
解析:设第n年获利y元,则y=20×1. 2n,n∈N*,2022年即第1年,20×1. 2n>60,n>log1. 23==
≈6. 03,所以n≥7,即从2028年开始这家加工厂年获利超过60万元. 故选C.
3. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系:
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p,则x,p分别为 ( B )
A.35,225 B.40,300
C.45,350 D.45,400
解析:在平面直角坐标系中画出表格中的各点,如图,
猜测为一次函数,故设y=kx+b(k,b为常数),将(30,60)和(40,30)代入得
解得故y=-3x+150,30≤x≤50,把点(45,15)和(50,0)代入解析式验证,检验成立.
则日销售利润P=(x-30)(-3x+150)=-3x2+240x-4 500,30≤x≤50,当取x=-=40∈[30,50]时, 日销售利润最大为300元. 故选B.
4. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费. 某职工某月缴水费16m元,则该职工这个月实际用水为 ( A )
A.13立方米 B.14立方米
C.18立方米 D.26立方米
解析:设职工的用水量为x立方米,需要交纳的水费为f(x)元,
当0≤x≤10时,f(x)=mx,当x>10时,f(x)=10×m+(x-10)×2m=2mx-10m,即函数的解析式为f(x)=
据此分类讨论:
当0≤x≤10时,mx=16m,解得x=16,不合题意,舍去;
当x>10时,2mx-10m=16m,解得x=13,符合题意;
综上可得,该职工这个月实际用水为13立方米. 故选A.
5. 已知光通过一块某种玻璃,强度要损失10%. 那么要使光的强度减弱到原来的以下,则至少需要通过这样的玻璃(参考数据:lg 3≈0. 477 1,lg 2≈0. 301 0) ( B )
A.6块 B.7块 C.8块 D.9块
解析:由题意知,经过n块玻璃后光的强度可记为f(n)=0. 9n(n∈N*),要使光的强度减弱到原来的以下,即f(n)=0. 9n< n>log0. 9≈6. 6,即n≥7. 故选B.
6. 2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5 000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除:(3)专项附加扣除包括①赡养老人费用,②子女教育费用,③继续教育费用,④大病医疗费用等. 其中前两项的扣除标准为①赡养老人费用:每月扣除2 000元,②子女教育费用:每个子女每月扣除1 000元.
新的个税政策的税率表部分内容如下:
级数 一级 二级 三级 …
每月应纳税所得额x元(含税) x≤3 000 3 000<x≤12 000 12 000<x≤25 000 …
税率(%) 3 10 20 …
现有李某月收入为19 000元,膝下有一名子女,需赡养老人(除此之外无其他专项附加扣除),则他该月应交纳的个税金额为 ( B )
A.570 B.890
C.1 100 D.1 900
解析:由题意,李某月应纳税所得额(含税)为19 000-5 000-1 000-2 000=11 000(元),
不超过3 000的部分的税额为3 000×3%=90(元),
超过3 000元至12 000元的部分税额为8 000×10%=800(元),所以李某该月应交纳的个税金额为90+800=890(元). 故选B.
7. 某游轮在A处看灯塔B在A的北偏东75°方向上,距离为12海里,灯塔C在A的北偏西30°方向上,距离为8海里. 游轮由A向正北方向航行到D处时,再看灯塔B在D的南偏东60°方向上,则C与D的距离为 ( B )
A.20海里 B.8海里
C.23海里 D.24海里
解析:根据题意画出示意图,如图. 在△ABD中,
∵∠DAB=75°,∠ADB=60°,AB=12,∴∠B=180°-75°-60°=45°.
由正弦定理得,
∴AD==24.
在△ACD中,AD=24,AC=8,∠CAD=30°,∴由余弦定理,得CD2=AD2+AC2-2AD·ACcos∠CAD=242+(8)2-2×24×8=192,∴CD=8. 故选B.
8. (多选题)如下图, △OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t<2)左侧的图形的面积为f(t),现给出函数f(t)的四个性质,其中说法正确的是 ( BD )
A.f
B.f(t)在(0,2)上单调递增
C.当t=1时,f(t)取得最大值
D.对于任意的t∈(0,2),都有f(t)+f(2-t)=
解析:由题可知,OB所在直线为y=x,AB所在直线为y=2x,
则当0<t≤1时,f(t)=t·t2;
当1<t<2时,f(t)=×22-(2-t)(2t)=-t2+2;则f(t)=
对于A,当t=时,f,故A错误;对于B,易知,f(t)在(0,1]上单调递增,在(1,2)上单调递增,且×12=×12+2×1-,则f(t)在(0,2)上单调递增,故B正确;对于C,因为f(t)在(0,2)上单调递增,则无最大值,故C错误;对于D,由题意知,当1<t<2时,f(t)=-t2+2(t-2)2+,
当0<t<1时,1<2-t<2,则f(t)+f(2-t)=t2-[(2-t)-2]2+,
当1<t<2时,0<2-t<1,则f(2-t)+f(t)=(2-t)2-(t-2)2+,
当t=1时,2-t=1,则f(t)+f(2-t)=2f(1)=2××12=,故D正确. 故选BD.
二、填空题
9. 某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2. 718…自然对数的底数,k,b为常数),若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是24小时.
解析:由题意可得,当x=0时,y=192;当x=22时,y=48,代入函数y=ekx+b,可得即则当x=33时,y=e33k+b=×192=24(小时).
10. 某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0. 01%,若初始时含杂质0. 2%,每次过滤可使杂质含量减少三分之一,则应过滤8次才能使得这种液体达到要求. (已知lg 2≈0. 301 0,lg 3≈0. 477 1)
解析:设过滤n次才能达到要求,则,即,
所以n×lg≤lg,即n≥≈7. 4,又∵n∈N,∴取n=8,即至少要过滤8次才能达到要求.
11. 学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50). 根据专家研究,当注意力指数大于62时,学习效果最佳. 要使得学生学习效果最佳,则教师安排核心内容的时间段为(4,28). (写成区间形式)
解析:当x∈(0,12]时,设f(x)=a(x-10)2+80,过点(12,78),代入,解得a=-,
则f(x)=-(x-10)2+80.
当x∈(12,40]时,设y=kx+b,过点B(12,78),C(40,50),得即y=-x+90,
由题意得或
解得4<x≤12或12<x<28,所以4<x<28,
则老师在x∈(4,28)时段内安排核心内容,能使得学生学习效果最佳.
三、解答题
12. 某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止,供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100. 水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨. 若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出
解:设进水量选为第x级,则t小时后水塔中水的剩余量为y=100+10xt-10t-100,且0≤t≤16.
由题意得0<y≤300,所以0<100+10xt-10t-100≤300.
当t=0时,结论成立.
当t>0时,由不等式100+10xt-10t-100>0可得x>1+10.
令f(t)=1+10,
则f(t)=-10+3. 5,
由于0≤t≤16,所以当t=4时,f(t)取最大值3. 5. 故x>3. 5.
又由100+10xt-10t-100≤300可得x≤1+.
令g(t)=1+,由于0<t≤16,所以当t=16时,g(t)取最小值4. 75,
故3. 5<x≤4. 75,由于x∈N*,
所以x=4.
即进水量选为第4级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出.
13. 某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 1~50 51~100 100以上
门票价格 13元/人 11元/人 9元/人
两个旅游团队计划游览该景点. 若分别购票,则共需支付门票费1 290元;若合并成一个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为 ( B )
A.20 B.30 C.35 D.40
解析:设两个旅游团队的人数分别为a,b,因为990不能被13整除,所以两个旅游团队人数之和a+b≥51,若51≤a+b≤100,则11(a+b)=990,得a+b=90 ①. 当a>50时,b<40,则11a+13b=1 290 ②,由①②得b=150,a=-60,不符合题意. 当a<50,b<50时,13(a+b)=1 290,易知该式不成立. 若a+b>100,则9(a+b)=990,得a+b=110 ③,当a≤50,51≤b≤100时,得13a+11b=1 290 ④,由③④得a=40,b=70. 当a≤50,b>100时,13a+9b=1 290 ⑤,由③⑤得,a=75,b=35,矛盾. 当51≤a≤100,51≤b≤100时,11(a+b)=1 290,易知该式不成立. 所以这两个旅游团队的人数之差为70-40=30. 故选B.
14. 近年来,我国在航天领域取得了巨大成就,得益于我国先进的运载火箭技术. 据了解,在不考虑空气阻力和地球引力的理想状态下,可以用公式v=v0ln计算火箭的最大速度v m/s,其中v0 m/s是喷流相对速度,m kg是火箭(除推进剂外)的质量,M kg是推进剂与火箭质量的总和,称为“总质比”. 已知A型火箭的喷流相对速度为2 000 m/s. 经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的1. 5倍,总质比变为原来的,若要使火箭的最大速度至少增加800 m/s,则在材料更新和技术改进前总质比的最小整数值为279. (参考数据:ln 330≈5. 8,2. 225<e0. 8<2. 226)
解析:由题意,经过材料更新和技术改进后,A型火箭的喷流相对速度为3 000 m/s,总质比变为. 要使火箭的最大速度至少增加800 m/s,则需3 000ln-2 000ln≥800,化简得3ln-2ln≥0. 8.
∴ln-ln≥0. 8,
整理得ln≥0. 8.
∴≥e0. 8,则≥125×e0. 8.
由参考数据,知2. 225<e0. 8<2. 226.
∴278. 125<125×e0. 8<278. 25.
∴材料更新和技术改进前总质比的最小整数值为279.
15. 某企业参加A项目生产的工人为1 000人,平均每人每年创造利润10万元. 根据现实的需要,从A项目中调出x人参与B项目的售后服务工作,每人每年可以创造利润10万元(a>0),A项目余下的工人每人每年创造利润将提高0. 2x%.
(1)若要保证A项目余下的工人创造的年总利润不低于原来1 000名工人创造的年总利润,则最多调出多少人参加B项目从事售后服务工作
(2)在(1)的条件下,当从A项目调出的人数不能超过总人数的40%时,才能使得A项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数a的取值范围.
解:设调出x人参加B项目从事售后服务工作.
(1)由题意得10(1 000-x)(1+0. 2x%)≥10×1 000,
即x2-500x≤0,又x>0,所以0<x≤500. 即最多调出500名员工从事B项目售后服务工作.
(2)由题知,0<x≤400,
从事B项目售后服务工作的员工创造的年总利润为10x万元,从事A项目的员工的年总利润为
10(1 000-x)万元,则
10x≤10(1 000-x)(1+0. 2x%),
所以ax-≤1 000+2x-x-x2,
所以ax≤+1 000+x,即a≤+1恒成立,
因为0<x≤400,
所以+1≥+1=5. 1,所以a≤5. 1,
又a>0,所以0<a≤5. 1,
即a的取值范围为(0,5. 1].
第四章量课时作业32数学建模活动(三)(原卷版)
一、选择题
1. 若矩形ABCD的一边长为x,周长为20,则当矩形面积最大时,x= ( C )
A.3 B.4
C.5 D.16
2. 某食品加工厂2021年获利20万元,经调整食品结构,开发新产品. 计划从2022年开始每年比上一年获利增加20%,问从哪一年开始这家加工厂年获利超过60万元(已知lg 2≈0. 301 0,lg 3≈0. 477 1). ( C )
A.2026年 B.2027年
C.2028年 D.2029年
3. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系:
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p,则x,p分别为 ( B )
A.35,225 B.40,300
C.45,350 D.45,400
4. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费. 某职工某月缴水费16m元,则该职工这个月实际用水为 ( A )
A.13立方米 B.14立方米
C.18立方米 D.26立方米
5. 已知光通过一块某种玻璃,强度要损失10%. 那么要使光的强度减弱到原来的以下,则至少需要通过这样的玻璃(参考数据:lg 3≈0. 477 1,lg 2≈0. 301 0) ( B )
A.6块 B.7块 C.8块 D.9块
6. 2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5 000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除:(3)专项附加扣除包括①赡养老人费用,②子女教育费用,③继续教育费用,④大病医疗费用等. 其中前两项的扣除标准为①赡养老人费用:每月扣除2 000元,②子女教育费用:每个子女每月扣除1 000元.
新的个税政策的税率表部分内容如下:
级数 一级 二级 三级 …
每月应纳税所得额x元(含税) x≤3 000 3 000<x≤12 000 12 000<x≤25 000 …
税率(%) 3 10 20 …
现有李某月收入为19 000元,膝下有一名子女,需赡养老人(除此之外无其他专项附加扣除),则他该月应交纳的个税金额为 ( B )
A.570 B.890
C.1 100 D.1 900
7. 某游轮在A处看灯塔B在A的北偏东75°方向上,距离为12海里,灯塔C在A的北偏西30°方向上,距离为8海里. 游轮由A向正北方向航行到D处时,再看灯塔B在D的南偏东60°方向上,则C与D的距离为 ( B )
A.20海里 B.8海里
C.23海里 D.24海里
8. (多选题)如下图, △OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t<2)左侧的图形的面积为f(t),现给出函数f(t)的四个性质,其中说法正确的是 ( BD )
A.f
B.f(t)在(0,2)上单调递增
C.当t=1时,f(t)取得最大值
D.对于任意的t∈(0,2),都有f(t)+f(2-t)=
二、填空题
9. 某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2. 718…自然对数的底数,k,b为常数),若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是24 小时.
10. 某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0. 01%,若初始时含杂质0. 2%,每次过滤可使杂质含量减少三分之一,则应过滤8 次才能使得这种液体达到要求. (已知lg 2≈0. 301 0,lg 3≈0. 477 1)
11. 学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50). 根据专家研究,当注意力指数大于62时,学习效果最佳. 要使得学生学习效果最佳,则教师安排核心内容的时间段为(4,28). (写成区间形式)
三、解答题
12. 某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止,供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100. 水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨. 若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出
13. 某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 1~50 51~100 100以上
门票价格 13元/人 11元/人 9元/人
两个旅游团队计划游览该景点. 若分别购票,则共需支付门票费1 290元;若合并成一个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为 ( B )
A.20 B.30 C.35 D.40
14. 近年来,我国在航天领域取得了巨大成就,得益于我国先进的运载火箭技术. 据了解,在不考虑空气阻力和地球引力的理想状态下,可以用公式v=v0ln计算火箭的最大速度v m/s,其中v0 m/s是喷流相对速度,m kg是火箭(除推进剂外)的质量,M kg是推进剂与火箭质量的总和,称为“总质比”. 已知A型火箭的喷流相对速度为2 000 m/s. 经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的1. 5倍,总质比变为原来的,若要使火箭的最大速度至少增加800 m/s,则在材料更新和技术改进前总质比的最小整数值为279. (参考数据:ln 330≈5. 8,2. 225<e0. 8<2. 226).
15. 某企业参加A项目生产的工人为1 000人,平均每人每年创造利润10万元. 根据现实的需要,从A项目中调出x人参与B项目的售后服务工作,每人每年可以创造利润10万元(a>0),A项目余下的工人每人每年创造利润将提高0. 2x%.
(1)若要保证A项目余下的工人创造的年总利润不低于原来1 000名工人创造的年总利润,则最多调出多少人参加B项目从事售后服务工作
(2)在(1)的条件下,当从A项目调出的人数不能超过总人数的40%时,才能使得A项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数a的取值范围.
北师大高中数学选择性必修第一册
第四章量课时作业32数学建模活动(三)(解析版)
一、选择题
1. 若矩形ABCD的一边长为x,周长为20,则当矩形面积最大时,x= ( C )
A.3 B.4
C.5 D.16
解析:矩形另一边长为=10-x,且有0<x<10,面积为f(x)=x(10-x)=-(x-5)2+25,所以,当x=5时,y=f(x)取最大值. 故选C.
2. 某食品加工厂2021年获利20万元,经调整食品结构,开发新产品. 计划从2022年开始每年比上一年获利增加20%,问从哪一年开始这家加工厂年获利超过60万元(已知lg 2≈0. 301 0,lg 3≈0. 477 1). ( C )
A.2026年 B.2027年
C.2028年 D.2029年
解析:设第n年获利y元,则y=20×1. 2n,n∈N*,2022年即第1年,20×1. 2n>60,n>log1. 23==
≈6. 03,所以n≥7,即从2028年开始这家加工厂年获利超过60万元. 故选C.
3. 某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系:
x … 30 40 45 50 …
y … 60 30 15 0 …
销售单价为x元时,才能获得最大日销售利润p,则x,p分别为 ( B )
A.35,225 B.40,300
C.45,350 D.45,400
解析:在平面直角坐标系中画出表格中的各点,如图,
猜测为一次函数,故设y=kx+b(k,b为常数),将(30,60)和(40,30)代入得
解得故y=-3x+150,30≤x≤50,把点(45,15)和(50,0)代入解析式验证,检验成立.
则日销售利润P=(x-30)(-3x+150)=-3x2+240x-4 500,30≤x≤50,当取x=-=40∈[30,50]时, 日销售利润最大为300元. 故选B.
4. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费. 某职工某月缴水费16m元,则该职工这个月实际用水为 ( A )
A.13立方米 B.14立方米
C.18立方米 D.26立方米
解析:设职工的用水量为x立方米,需要交纳的水费为f(x)元,
当0≤x≤10时,f(x)=mx,当x>10时,f(x)=10×m+(x-10)×2m=2mx-10m,即函数的解析式为f(x)=
据此分类讨论:
当0≤x≤10时,mx=16m,解得x=16,不合题意,舍去;
当x>10时,2mx-10m=16m,解得x=13,符合题意;
综上可得,该职工这个月实际用水为13立方米. 故选A.
5. 已知光通过一块某种玻璃,强度要损失10%. 那么要使光的强度减弱到原来的以下,则至少需要通过这样的玻璃(参考数据:lg 3≈0. 477 1,lg 2≈0. 301 0) ( B )
A.6块 B.7块 C.8块 D.9块
解析:由题意知,经过n块玻璃后光的强度可记为f(n)=0. 9n(n∈N*),要使光的强度减弱到原来的以下,即f(n)=0. 9n< n>log0. 9≈6. 6,即n≥7. 故选B.
6. 2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5 000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除:(3)专项附加扣除包括①赡养老人费用,②子女教育费用,③继续教育费用,④大病医疗费用等. 其中前两项的扣除标准为①赡养老人费用:每月扣除2 000元,②子女教育费用:每个子女每月扣除1 000元.
新的个税政策的税率表部分内容如下:
级数 一级 二级 三级 …
每月应纳税所得额x元(含税) x≤3 000 3 000<x≤12 000 12 000<x≤25 000 …
税率(%) 3 10 20 …
现有李某月收入为19 000元,膝下有一名子女,需赡养老人(除此之外无其他专项附加扣除),则他该月应交纳的个税金额为 ( B )
A.570 B.890
C.1 100 D.1 900
解析:由题意,李某月应纳税所得额(含税)为19 000-5 000-1 000-2 000=11 000(元),
不超过3 000的部分的税额为3 000×3%=90(元),
超过3 000元至12 000元的部分税额为8 000×10%=800(元),所以李某该月应交纳的个税金额为90+800=890(元). 故选B.
7. 某游轮在A处看灯塔B在A的北偏东75°方向上,距离为12海里,灯塔C在A的北偏西30°方向上,距离为8海里. 游轮由A向正北方向航行到D处时,再看灯塔B在D的南偏东60°方向上,则C与D的距离为 ( B )
A.20海里 B.8海里
C.23海里 D.24海里
解析:根据题意画出示意图,如图. 在△ABD中,
∵∠DAB=75°,∠ADB=60°,AB=12,∴∠B=180°-75°-60°=45°.
由正弦定理得,
∴AD==24.
在△ACD中,AD=24,AC=8,∠CAD=30°,∴由余弦定理,得CD2=AD2+AC2-2AD·ACcos∠CAD=242+(8)2-2×24×8=192,∴CD=8. 故选B.
8. (多选题)如下图, △OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t<2)左侧的图形的面积为f(t),现给出函数f(t)的四个性质,其中说法正确的是 ( BD )
A.f
B.f(t)在(0,2)上单调递增
C.当t=1时,f(t)取得最大值
D.对于任意的t∈(0,2),都有f(t)+f(2-t)=
解析:由题可知,OB所在直线为y=x,AB所在直线为y=2x,
则当0<t≤1时,f(t)=t·t2;
当1<t<2时,f(t)=×22-(2-t)(2t)=-t2+2;则f(t)=
对于A,当t=时,f,故A错误;对于B,易知,f(t)在(0,1]上单调递增,在(1,2)上单调递增,且×12=×12+2×1-,则f(t)在(0,2)上单调递增,故B正确;对于C,因为f(t)在(0,2)上单调递增,则无最大值,故C错误;对于D,由题意知,当1<t<2时,f(t)=-t2+2(t-2)2+,
当0<t<1时,1<2-t<2,则f(t)+f(2-t)=t2-[(2-t)-2]2+,
当1<t<2时,0<2-t<1,则f(2-t)+f(t)=(2-t)2-(t-2)2+,
当t=1时,2-t=1,则f(t)+f(2-t)=2f(1)=2××12=,故D正确. 故选BD.
二、填空题
9. 某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2. 718…自然对数的底数,k,b为常数),若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是24小时.
解析:由题意可得,当x=0时,y=192;当x=22时,y=48,代入函数y=ekx+b,可得即则当x=33时,y=e33k+b=×192=24(小时).
10. 某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0. 01%,若初始时含杂质0. 2%,每次过滤可使杂质含量减少三分之一,则应过滤8次才能使得这种液体达到要求. (已知lg 2≈0. 301 0,lg 3≈0. 477 1)
解析:设过滤n次才能达到要求,则,即,
所以n×lg≤lg,即n≥≈7. 4,又∵n∈N,∴取n=8,即至少要过滤8次才能达到要求.
11. 学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50). 根据专家研究,当注意力指数大于62时,学习效果最佳. 要使得学生学习效果最佳,则教师安排核心内容的时间段为(4,28). (写成区间形式)
解析:当x∈(0,12]时,设f(x)=a(x-10)2+80,过点(12,78),代入,解得a=-,
则f(x)=-(x-10)2+80.
当x∈(12,40]时,设y=kx+b,过点B(12,78),C(40,50),得即y=-x+90,
由题意得或
解得4<x≤12或12<x<28,所以4<x<28,
则老师在x∈(4,28)时段内安排核心内容,能使得学生学习效果最佳.
三、解答题
12. 某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止,供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100. 水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨. 若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出
解:设进水量选为第x级,则t小时后水塔中水的剩余量为y=100+10xt-10t-100,且0≤t≤16.
由题意得0<y≤300,所以0<100+10xt-10t-100≤300.
当t=0时,结论成立.
当t>0时,由不等式100+10xt-10t-100>0可得x>1+10.
令f(t)=1+10,
则f(t)=-10+3. 5,
由于0≤t≤16,所以当t=4时,f(t)取最大值3. 5. 故x>3. 5.
又由100+10xt-10t-100≤300可得x≤1+.
令g(t)=1+,由于0<t≤16,所以当t=16时,g(t)取最小值4. 75,
故3. 5<x≤4. 75,由于x∈N*,
所以x=4.
即进水量选为第4级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出.
13. 某旅游景点为吸引游客,推出团体购票优惠方案如下表:
购票人数 1~50 51~100 100以上
门票价格 13元/人 11元/人 9元/人
两个旅游团队计划游览该景点. 若分别购票,则共需支付门票费1 290元;若合并成一个团队购票,则需支付门票费990元,那么这两个旅游团队的人数之差为 ( B )
A.20 B.30 C.35 D.40
解析:设两个旅游团队的人数分别为a,b,因为990不能被13整除,所以两个旅游团队人数之和a+b≥51,若51≤a+b≤100,则11(a+b)=990,得a+b=90 ①. 当a>50时,b<40,则11a+13b=1 290 ②,由①②得b=150,a=-60,不符合题意. 当a<50,b<50时,13(a+b)=1 290,易知该式不成立. 若a+b>100,则9(a+b)=990,得a+b=110 ③,当a≤50,51≤b≤100时,得13a+11b=1 290 ④,由③④得a=40,b=70. 当a≤50,b>100时,13a+9b=1 290 ⑤,由③⑤得,a=75,b=35,矛盾. 当51≤a≤100,51≤b≤100时,11(a+b)=1 290,易知该式不成立. 所以这两个旅游团队的人数之差为70-40=30. 故选B.
14. 近年来,我国在航天领域取得了巨大成就,得益于我国先进的运载火箭技术. 据了解,在不考虑空气阻力和地球引力的理想状态下,可以用公式v=v0ln计算火箭的最大速度v m/s,其中v0 m/s是喷流相对速度,m kg是火箭(除推进剂外)的质量,M kg是推进剂与火箭质量的总和,称为“总质比”. 已知A型火箭的喷流相对速度为2 000 m/s. 经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的1. 5倍,总质比变为原来的,若要使火箭的最大速度至少增加800 m/s,则在材料更新和技术改进前总质比的最小整数值为279. (参考数据:ln 330≈5. 8,2. 225<e0. 8<2. 226)
解析:由题意,经过材料更新和技术改进后,A型火箭的喷流相对速度为3 000 m/s,总质比变为. 要使火箭的最大速度至少增加800 m/s,则需3 000ln-2 000ln≥800,化简得3ln-2ln≥0. 8.
∴ln-ln≥0. 8,
整理得ln≥0. 8.
∴≥e0. 8,则≥125×e0. 8.
由参考数据,知2. 225<e0. 8<2. 226.
∴278. 125<125×e0. 8<278. 25.
∴材料更新和技术改进前总质比的最小整数值为279.
15. 某企业参加A项目生产的工人为1 000人,平均每人每年创造利润10万元. 根据现实的需要,从A项目中调出x人参与B项目的售后服务工作,每人每年可以创造利润10万元(a>0),A项目余下的工人每人每年创造利润将提高0. 2x%.
(1)若要保证A项目余下的工人创造的年总利润不低于原来1 000名工人创造的年总利润,则最多调出多少人参加B项目从事售后服务工作
(2)在(1)的条件下,当从A项目调出的人数不能超过总人数的40%时,才能使得A项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数a的取值范围.
解:设调出x人参加B项目从事售后服务工作.
(1)由题意得10(1 000-x)(1+0. 2x%)≥10×1 000,
即x2-500x≤0,又x>0,所以0<x≤500. 即最多调出500名员工从事B项目售后服务工作.
(2)由题知,0<x≤400,
从事B项目售后服务工作的员工创造的年总利润为10x万元,从事A项目的员工的年总利润为
10(1 000-x)万元,则
10x≤10(1 000-x)(1+0. 2x%),
所以ax-≤1 000+2x-x-x2,
所以ax≤+1 000+x,即a≤+1恒成立,
因为0<x≤400,
所以+1≥+1=5. 1,所以a≤5. 1,
又a>0,所以0<a≤5. 1,
即a的取值范围为(0,5. 1].
同课章节目录
