第二章 整式的加减 测试卷(含答案) 2023— 2024学年人教版数学七年级上册
文档属性
| 名称 | 第二章 整式的加减 测试卷(含答案) 2023— 2024学年人教版数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 21:25:24 | ||
图片预览



文档简介
第二章测试卷 (时间:120分钟 满分:150分)
一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案填在题后对应的括号内.
1.整式-3xy2的系数是( )
A.-3 B.3 C.-3x D.3x
2.下列代数式,-xy,,0,x+2y,y中,单项式有( )
A.5个 B.2个
C.3个 D.4个
3.下列说法正确的是( )
A.2πmn的系数是2π B.-82ab2的次数是5次
C.xy3+3x2y-4的常数项为4 D.11x2-6x+5是三次三项式
4.下列各式中,运算正确的是( )
A.a2+a2=a4 B.2a2+b3=2a2b3
C.-2a2b+2ba2=0 D.2a2-a2=2
5.我校给某“希望小学”邮寄每册a元的图书1 000册,若每册图书的邮费是书价的5%,则共需邮费( )
A.5%a元 B.5%×1 000a元
C.1 000a(1+5%)元 D.50元
6.下列去括号正确的是( )
A.a-(b-c)=a-b-c B.x2-[-(-x+y)]=x2-x+y
C.m-2(p-q)=m-2p D.a+(b-c-2d)=a+b-c+2d
7.李老师做了一个长方形教具,其中一边长为2a+b,另一边长为a-b,则该长方形周长为( )
A.6a+b B.6a
C.3a D.10a-b
8.若代数式-xa+1y3与-ybx2的和是单项式,则2a-b的值为( )
A.-1 B.3
C.1 D.0
9.一个多项式与x2+2x+1的和是3x-2,则这个多项式为( )
A.x2-5x+3 B.-x2+x-3
C.-x2+5x-3 D.x2-5x-13
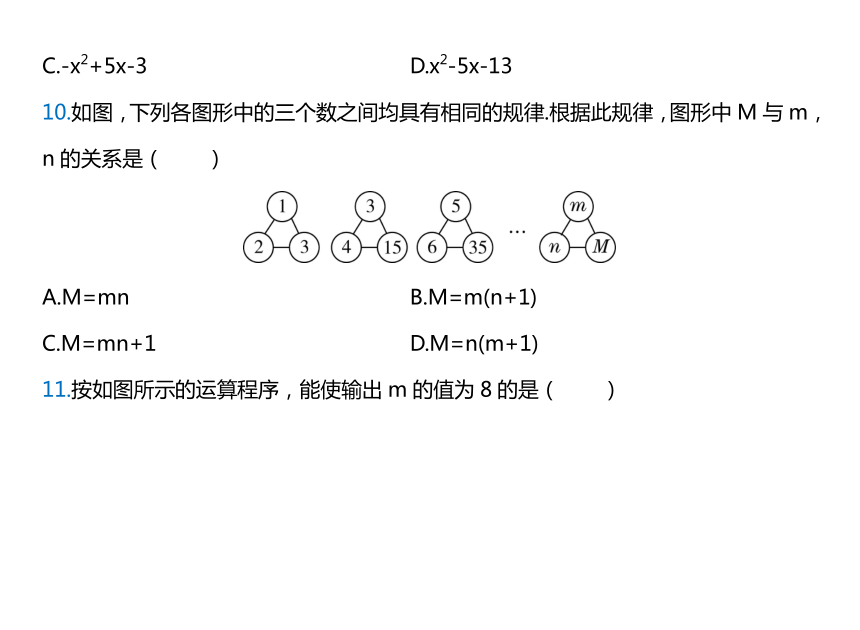
10.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m,n的关系是( )
A.M=mn B.M=m(n+1)
C.M=mn+1 D.M=n(m+1)
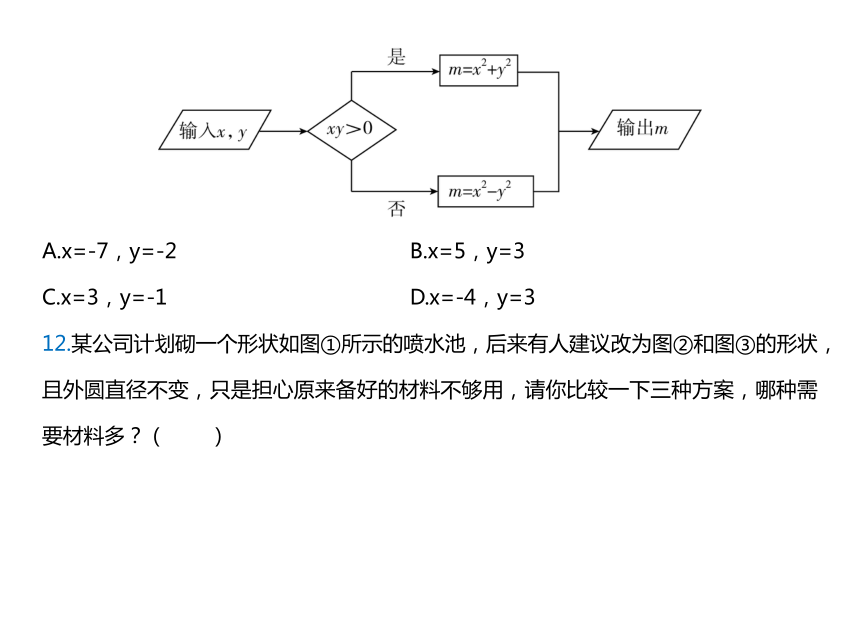
11.按如图所示的运算程序,能使输出m的值为8的是( )
A.x=-7,y=-2 B.x=5,y=3
C.x=3,y=-1 D.x=-4,y=3
12.某公司计划砌一个形状如图①所示的喷水池,后来有人建议改为图②和图③的形状,且外圆直径不变,只是担心原来备好的材料不够用,请你比较一下三种方案,哪种需要材料多?( )
A.图①多 B.图②多
C.图③多 D.图①、图②、图③一样多
二、填空题(本大题4个小题,每小题4分,共16分)请将答案填在横线上.
13.某花店新开张,第一天销售盆栽m盆,第二天比第一天多销售7盆,第三天的销售量是第二天的3倍少13盆,则第三天销售了 盆.(结果用含m的式子表示)
14.观察下列单项式:3a2,5a5,7a10,9a17,11a26,…,它们是按一定规律排列的,那么这列式子的第n个单项式是 .
15.若x2-2y+3=0,则-2x2+4y+12的值为 .
16.观察下列等式:
第1个等式:a1==× ;
第2个等式:a2==× ;
第3个等式:a3==× ;
….
按以上规律,若a1+a2+a3+…+an=,则n的值为 .
三、解答题(本大题共9个小题,17、18题各8分,19至25题每题10分,共86分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形.
17.合并同类项:
(1)(2xy-y)-(-y+xy); (2)(3a2-ab+7)-(-4a2+2ab+7).
18.合并同类项:
(1)x+2(x-y2)+(1-y2); (2)3x2y+[xy2-2(2xy2-3x2y)].
19.先化简,再求值:
已知2(-3xy+x2)-[2x2-3(5xy-2x2)-xy],其中x,y满足|x+2|+(y-3)2=0.
20.新一轮强降雨导致多地受灾,为帮助灾区民众渡过难关,某学校七年级两个班的115名学生积极参与,踊跃捐款.已知甲班有的学生每人捐了10元,乙班有的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人.
(1)用含x的代数式表示乙班人数;
(2)用含x的代数式表示两班捐款的总额;
(3)若x=60,则两班共捐款多少元?
21.如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
(1)在第4个图中,共有白色瓷砖 块;在第n个图中,共有白色瓷砖
块;
(2)试用含n的代数式表示在第n个图中共有瓷砖的块数;
(3)如果每块黑瓷砖35元,每块白瓷砖50元,当n=10时,求铺设长方形地面共需花多少钱购买瓷砖?
22.已知多项式(ax3-3x-6y+a)-(2x3+bx+y+1).
(1)若此多项式的值与x的取值无关,求a,b的值;
(2)在(1)的条件下,先化简多项式(4a2+2ab-b2)-3(a2-ab+b2),再求值.
23.阅读下面材料,解决后面的问题.
一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,如果a+b=c+d,那么我们把这个四位正整数叫做“对头数”.例如四位正整数2 947,因为2+9=4+7,所以2 947叫做“对头数”.
(1)判断8 127和3 456是不是“对头数”,并说明理由;
(2)已知一个四位正整数的个位上的数字是5,百位上的数字是3,若这个正整数是“对头数”,且这个正整数能被7整除,求这个正整数.
24.阅读下列材料.
让我们规定一种运算=ad-cb,如=2×5-3×4=-2,再如 =4x-2.
按照这种运算规定,请解答下列问题.
(1)计算 = , = , = ;
(2)当x=-1时,求 的值(要求写出计算过程).
25.已知多项式2x3y-xy+16的次数为a,常数项为b.a,b分别对应着数轴上的A,B两点.
(1)a= ,b= ;并在数轴上画出A,B两点.
(2)若点P从点A出发,以每秒3个单位长度的速度向x轴正半轴运动,运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍?
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动到终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.
1.A
2.D
3.A
4.C
5.B
6.B
7.B
8.A
9.B
10.B
11.C
12.D
13. (3m+8)
14. (2n+1)an2+1
15. 18
16. 49
17.(1)解:原式=2xy-y+y-xy
=xy.
(2)解:原式=3a2-ab+7+4a2-2ab-7
=7a2-3ab.
18.(1)解:原式=x+2x-2y2+1-y2
=3x-3y2+1.
(2)解:原式=3x2y+(xy2-4xy2+6x2y)
=3x2y+xy2-4xy2+6x2y
=9x2y-3xy2.
19.解:原式=-6xy+2x2-(2x2-15xy+6x2-xy)
=-6xy+2x2-2x2+15xy-6x2+xy
=-6x2+10xy.
因为|x+2|+(y-3)2=0,所以x=-2,y=3.
所以原式=-6x2+10xy
=-6×(-2)2+10×(-2)×3
=-24-60
=-84.
20.解:(1)由题意可得,乙班人数为115-x.
(2)x×10+(115-x)×10+ x×5+ (115-x)×5
=x+460-4x+x+345-3x
=-x+805,
即两班捐款的总额是 元.
(3)当x=60时,
-x+805=-×60+805=-20+805=785(元),
x=60时,两班共捐款785元.
21.解:由图形排列规律发现:
第1个图形中有白色瓷砖1×3块,共有瓷砖3×5块;
第2个图形中有白色瓷砖2×4块,共有瓷砖4×6块;
第3个图形中有白色瓷砖3×5块,共有瓷砖5×7块.
(1)第4个图形中有白色瓷砖4×6=24块,第n个图形中有白色瓷砖n(n+2)块.
故答案为:24,n(n+2).
(2)共有瓷砖(n+2)(n+4)块.
(3)当n=10时,共有白色瓷砖120块,黑色瓷砖48块,
120×50+48×35=6 000+1 680=7 680(元).
22.解:(1)原式=ax3-3x-6y+a-2x3-bx-y-1
=(a-2)x3-(3+b)x-7y+a-1,
∵多项式的值与x的取值无关,∴a-2=0,b+3=0,
解得a=2,b=-3,
即a的值为2,b的值为-3.
(2)原式=4a2+2ab-b2-3a2+3ab-3b2=a2+5ab-4b2,
当a=2,b=-3时,
原式=22+5×2×(-3)-4×(-3)2
=4-30-4×9
=4-30-36
=-62.
23.解:(1)因为8+1=2+7,所以8 127是“对头数”;
因为3+4≠5+6,所以3 456不是“对头数”.
(2)设这个正整数千位上数字为b,十位数字为a,0≤a≤9,0≤b≤9,
根据这个正整数是“对头数”,得a+5=b+3,即b=a+2,
∴这个四位数为1 000b+300+10a+5
=1 000(a+2)+300+10a+5
=1 010a+2 305,
∵1 010=7×144……2,2 305=7×329……2,
∴1 010a+2 305
=(7×144+2)a+7×329+2
=7(144a+329)+2a+2,
∵这个四位数能被7整除,即这个四位数是7的倍数,
∴2a+2必须是7的倍数,
当2a+2=0,即a=-1时,不符合题意;
当2a+2=7,即a=2.5,不符合题意;
当2a+2=7×2,即a=6时,符合题意,此时b=8,即四位数为8 365;
当2a+2=7×3,即a=9.5,不符合题意;
综上所述,这个正整数为8 365.
24.解:(1) =6×-4×0.5=3-2=1;
=-3×5-4×(-2)=-15-(-8)=-7;
=2×(-5x)-3×(-3x)=-10x-(-9x)=-x.
(2)原式=(-3x2+2x+1)×(-2)-(-3)×(-2x2+x-2)
=(6x2-4x-2)-(6x2-3x+6)
=-x-8.
当x=-1时,原式=-x-8=-(-1)-8=-7.
4
16
25.解:(1)因为多项式2x3y-xy+16的次数为a,常数项为b,
所以a=4,b=16,
点A,B的位置如答图.
(2)设运动时间为t s.
由题意,得3t=2(16-4-3t)或3t=2(4+3t-16),
解得t=或8,
所以运动时间为秒或8秒时,点P到点A的距离是点P到点B的距离的2倍.
(3)设运动时间为t s.
由题意,得12+t-3t=4或3t-(12+t)=4或12+t+3t-4=52,
解得t=4或8或11,对应的点Q坐标为20,24或27.
所以点P和点Q运动4秒或8秒或11秒时,P,Q两点之间的距离为4,对应的点Q坐标为20,24或27.
一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案填在题后对应的括号内.
1.整式-3xy2的系数是( )
A.-3 B.3 C.-3x D.3x
2.下列代数式,-xy,,0,x+2y,y中,单项式有( )
A.5个 B.2个
C.3个 D.4个
3.下列说法正确的是( )
A.2πmn的系数是2π B.-82ab2的次数是5次
C.xy3+3x2y-4的常数项为4 D.11x2-6x+5是三次三项式
4.下列各式中,运算正确的是( )
A.a2+a2=a4 B.2a2+b3=2a2b3
C.-2a2b+2ba2=0 D.2a2-a2=2
5.我校给某“希望小学”邮寄每册a元的图书1 000册,若每册图书的邮费是书价的5%,则共需邮费( )
A.5%a元 B.5%×1 000a元
C.1 000a(1+5%)元 D.50元
6.下列去括号正确的是( )
A.a-(b-c)=a-b-c B.x2-[-(-x+y)]=x2-x+y
C.m-2(p-q)=m-2p D.a+(b-c-2d)=a+b-c+2d
7.李老师做了一个长方形教具,其中一边长为2a+b,另一边长为a-b,则该长方形周长为( )
A.6a+b B.6a
C.3a D.10a-b
8.若代数式-xa+1y3与-ybx2的和是单项式,则2a-b的值为( )
A.-1 B.3
C.1 D.0
9.一个多项式与x2+2x+1的和是3x-2,则这个多项式为( )
A.x2-5x+3 B.-x2+x-3
C.-x2+5x-3 D.x2-5x-13
10.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m,n的关系是( )
A.M=mn B.M=m(n+1)
C.M=mn+1 D.M=n(m+1)
11.按如图所示的运算程序,能使输出m的值为8的是( )
A.x=-7,y=-2 B.x=5,y=3
C.x=3,y=-1 D.x=-4,y=3
12.某公司计划砌一个形状如图①所示的喷水池,后来有人建议改为图②和图③的形状,且外圆直径不变,只是担心原来备好的材料不够用,请你比较一下三种方案,哪种需要材料多?( )
A.图①多 B.图②多
C.图③多 D.图①、图②、图③一样多
二、填空题(本大题4个小题,每小题4分,共16分)请将答案填在横线上.
13.某花店新开张,第一天销售盆栽m盆,第二天比第一天多销售7盆,第三天的销售量是第二天的3倍少13盆,则第三天销售了 盆.(结果用含m的式子表示)
14.观察下列单项式:3a2,5a5,7a10,9a17,11a26,…,它们是按一定规律排列的,那么这列式子的第n个单项式是 .
15.若x2-2y+3=0,则-2x2+4y+12的值为 .
16.观察下列等式:
第1个等式:a1==× ;
第2个等式:a2==× ;
第3个等式:a3==× ;
….
按以上规律,若a1+a2+a3+…+an=,则n的值为 .
三、解答题(本大题共9个小题,17、18题各8分,19至25题每题10分,共86分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形.
17.合并同类项:
(1)(2xy-y)-(-y+xy); (2)(3a2-ab+7)-(-4a2+2ab+7).
18.合并同类项:
(1)x+2(x-y2)+(1-y2); (2)3x2y+[xy2-2(2xy2-3x2y)].
19.先化简,再求值:
已知2(-3xy+x2)-[2x2-3(5xy-2x2)-xy],其中x,y满足|x+2|+(y-3)2=0.
20.新一轮强降雨导致多地受灾,为帮助灾区民众渡过难关,某学校七年级两个班的115名学生积极参与,踊跃捐款.已知甲班有的学生每人捐了10元,乙班有的学生每人捐了10元,两个班其余学生每人捐了5元,设甲班有学生x人.
(1)用含x的代数式表示乙班人数;
(2)用含x的代数式表示两班捐款的总额;
(3)若x=60,则两班共捐款多少元?
21.如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
(1)在第4个图中,共有白色瓷砖 块;在第n个图中,共有白色瓷砖
块;
(2)试用含n的代数式表示在第n个图中共有瓷砖的块数;
(3)如果每块黑瓷砖35元,每块白瓷砖50元,当n=10时,求铺设长方形地面共需花多少钱购买瓷砖?
22.已知多项式(ax3-3x-6y+a)-(2x3+bx+y+1).
(1)若此多项式的值与x的取值无关,求a,b的值;
(2)在(1)的条件下,先化简多项式(4a2+2ab-b2)-3(a2-ab+b2),再求值.
23.阅读下面材料,解决后面的问题.
一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,如果a+b=c+d,那么我们把这个四位正整数叫做“对头数”.例如四位正整数2 947,因为2+9=4+7,所以2 947叫做“对头数”.
(1)判断8 127和3 456是不是“对头数”,并说明理由;
(2)已知一个四位正整数的个位上的数字是5,百位上的数字是3,若这个正整数是“对头数”,且这个正整数能被7整除,求这个正整数.
24.阅读下列材料.
让我们规定一种运算=ad-cb,如=2×5-3×4=-2,再如 =4x-2.
按照这种运算规定,请解答下列问题.
(1)计算 = , = , = ;
(2)当x=-1时,求 的值(要求写出计算过程).
25.已知多项式2x3y-xy+16的次数为a,常数项为b.a,b分别对应着数轴上的A,B两点.
(1)a= ,b= ;并在数轴上画出A,B两点.
(2)若点P从点A出发,以每秒3个单位长度的速度向x轴正半轴运动,运动时间为多少时,点P到点A的距离是点P到点B的距离的2倍?
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P到达C点后,再立即以同样的速度返回,运动到终点A,求点P和点Q运动多少秒时,P,Q两点之间的距离为4,并求出此时点Q的坐标.
1.A
2.D
3.A
4.C
5.B
6.B
7.B
8.A
9.B
10.B
11.C
12.D
13. (3m+8)
14. (2n+1)an2+1
15. 18
16. 49
17.(1)解:原式=2xy-y+y-xy
=xy.
(2)解:原式=3a2-ab+7+4a2-2ab-7
=7a2-3ab.
18.(1)解:原式=x+2x-2y2+1-y2
=3x-3y2+1.
(2)解:原式=3x2y+(xy2-4xy2+6x2y)
=3x2y+xy2-4xy2+6x2y
=9x2y-3xy2.
19.解:原式=-6xy+2x2-(2x2-15xy+6x2-xy)
=-6xy+2x2-2x2+15xy-6x2+xy
=-6x2+10xy.
因为|x+2|+(y-3)2=0,所以x=-2,y=3.
所以原式=-6x2+10xy
=-6×(-2)2+10×(-2)×3
=-24-60
=-84.
20.解:(1)由题意可得,乙班人数为115-x.
(2)x×10+(115-x)×10+ x×5+ (115-x)×5
=x+460-4x+x+345-3x
=-x+805,
即两班捐款的总额是 元.
(3)当x=60时,
-x+805=-×60+805=-20+805=785(元),
x=60时,两班共捐款785元.
21.解:由图形排列规律发现:
第1个图形中有白色瓷砖1×3块,共有瓷砖3×5块;
第2个图形中有白色瓷砖2×4块,共有瓷砖4×6块;
第3个图形中有白色瓷砖3×5块,共有瓷砖5×7块.
(1)第4个图形中有白色瓷砖4×6=24块,第n个图形中有白色瓷砖n(n+2)块.
故答案为:24,n(n+2).
(2)共有瓷砖(n+2)(n+4)块.
(3)当n=10时,共有白色瓷砖120块,黑色瓷砖48块,
120×50+48×35=6 000+1 680=7 680(元).
22.解:(1)原式=ax3-3x-6y+a-2x3-bx-y-1
=(a-2)x3-(3+b)x-7y+a-1,
∵多项式的值与x的取值无关,∴a-2=0,b+3=0,
解得a=2,b=-3,
即a的值为2,b的值为-3.
(2)原式=4a2+2ab-b2-3a2+3ab-3b2=a2+5ab-4b2,
当a=2,b=-3时,
原式=22+5×2×(-3)-4×(-3)2
=4-30-4×9
=4-30-36
=-62.
23.解:(1)因为8+1=2+7,所以8 127是“对头数”;
因为3+4≠5+6,所以3 456不是“对头数”.
(2)设这个正整数千位上数字为b,十位数字为a,0≤a≤9,0≤b≤9,
根据这个正整数是“对头数”,得a+5=b+3,即b=a+2,
∴这个四位数为1 000b+300+10a+5
=1 000(a+2)+300+10a+5
=1 010a+2 305,
∵1 010=7×144……2,2 305=7×329……2,
∴1 010a+2 305
=(7×144+2)a+7×329+2
=7(144a+329)+2a+2,
∵这个四位数能被7整除,即这个四位数是7的倍数,
∴2a+2必须是7的倍数,
当2a+2=0,即a=-1时,不符合题意;
当2a+2=7,即a=2.5,不符合题意;
当2a+2=7×2,即a=6时,符合题意,此时b=8,即四位数为8 365;
当2a+2=7×3,即a=9.5,不符合题意;
综上所述,这个正整数为8 365.
24.解:(1) =6×-4×0.5=3-2=1;
=-3×5-4×(-2)=-15-(-8)=-7;
=2×(-5x)-3×(-3x)=-10x-(-9x)=-x.
(2)原式=(-3x2+2x+1)×(-2)-(-3)×(-2x2+x-2)
=(6x2-4x-2)-(6x2-3x+6)
=-x-8.
当x=-1时,原式=-x-8=-(-1)-8=-7.
4
16
25.解:(1)因为多项式2x3y-xy+16的次数为a,常数项为b,
所以a=4,b=16,
点A,B的位置如答图.
(2)设运动时间为t s.
由题意,得3t=2(16-4-3t)或3t=2(4+3t-16),
解得t=或8,
所以运动时间为秒或8秒时,点P到点A的距离是点P到点B的距离的2倍.
(3)设运动时间为t s.
由题意,得12+t-3t=4或3t-(12+t)=4或12+t+3t-4=52,
解得t=4或8或11,对应的点Q坐标为20,24或27.
所以点P和点Q运动4秒或8秒或11秒时,P,Q两点之间的距离为4,对应的点Q坐标为20,24或27.
