第三章 3.1.2 函数的表示方法第2课时 课件(共34张PPT)
文档属性
| 名称 | 第三章 3.1.2 函数的表示方法第2课时 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 22:52:35 | ||
图片预览









文档简介
(共34张PPT)
第三章
3.1.2函数的表示方法第2课时
人教A版(2019)
教学目标
学习目标 数学素养
1.明确函数的三种表示方法; 1.通过函数解析式,培养数学抽象素养;
2.在实际情境中,会根据不同需要选择恰当的方法表示函数; 2.利用函数图像培养数据分析素养;
3.通过具体实例,了解简单的分段函数,并能简单应用. 3.构建函数模型,培养数学建模素养.
知识回顾
1.函数的三种表示方法
表示法 定义
解析法 用___________表示两个变量之间的对应关系
图象法 用_________表示两个变量之间的对应关系
列表法 列出_________来表示两个变量之间的对应关系
数学表达式
图象
表格
温故知新
优点 缺点 联系
解 析 法 简明、全面地概括了变量间的对应关系;可以通过解析式求出任意自变量的值所对应的函数值. 形象性与直观性不足,变化趋势难判断,有些函数关系不能用解析式表示. 解析、列表和图象三种方法
各有优缺点,
面对实际问题时
根据需要恰当选择.
列 表 法 不需要计算就可以直接看出与自变量的值相对应的函数值. 只能列出部分自变量与函数的对应值,无法反映函数变化的全貌. 图 象 法 直观形象地表示随着自变量的变化,相应的函数值变化的趋势,有利于我们研究函数的某些性质. 只能近似得到数量关系,误差较大,容易误判断. 温故知新
2.分段函数
分段函数的定义域、值域分别是各段函数的定义域、值域的并集
(1)一般地,分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的 的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是 .
(3)作分段函数图象时,应分别作出每一段的图象.
对应关系
并集
空集
新知形成
课前测评
1.函数f(x)=3x-1,x∈[1,5]的图象是( )
A.直线 B.射线 C.线段 D.离散的点
解析 ∵f(x)=3x-1为一次函数,图象为一条直线,而x∈[1,5],则此时图象为线段.故选C.
新知形成
课前测评
3.已知f(x)的图象如图,则f(x)的值域为________.
解析 由f(x)的图象知,f(x)的值域为[-4,3].
新知形成
【例7】下表3.1-4是某校高一(1)班三名同学在高一学年度
六次数学测试的成绩及班级平均分表.
请你对这三们同学在高一学年度的数学学习情况做一个分析.
第一次 第二次 第三次 第四次 第五次 第六次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平均分 88.2 78.3 85.4 80.3 75.7 82.6
新知讲解
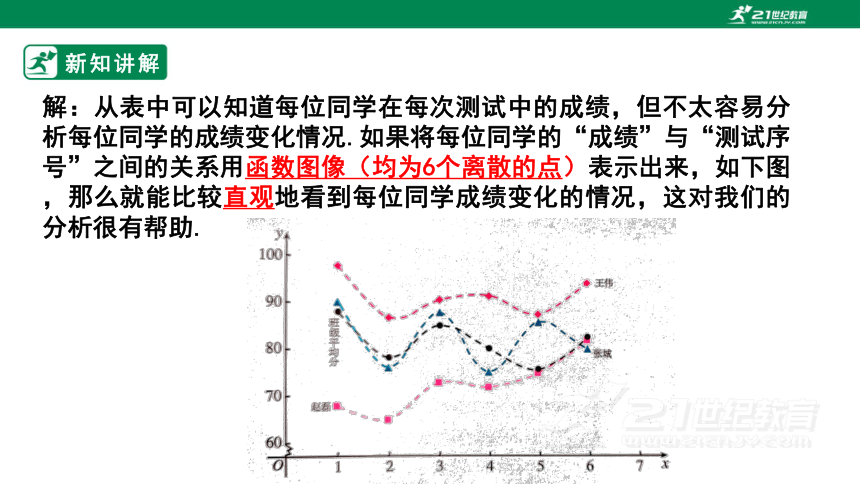
解:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将每位同学的“成绩”与“测试序号”之间的关系用函数图像(均为6个离散的点)表示出来,如下图,那么就能比较直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
新知讲解
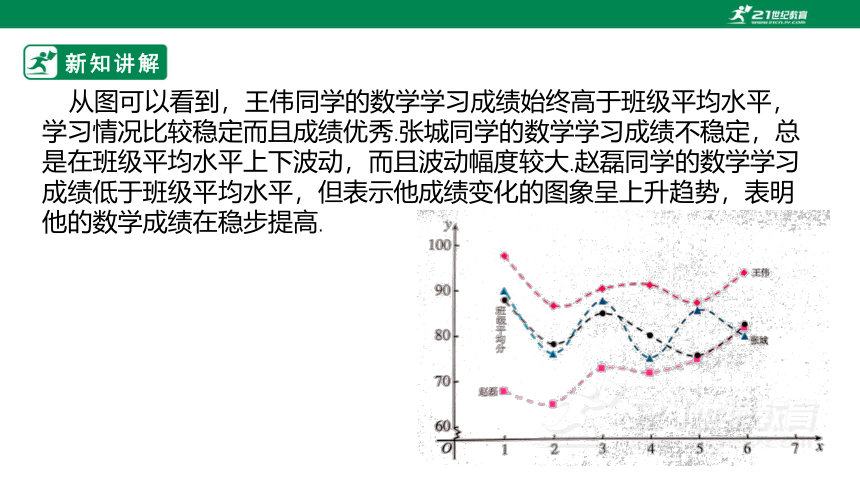
从图可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
初试身手
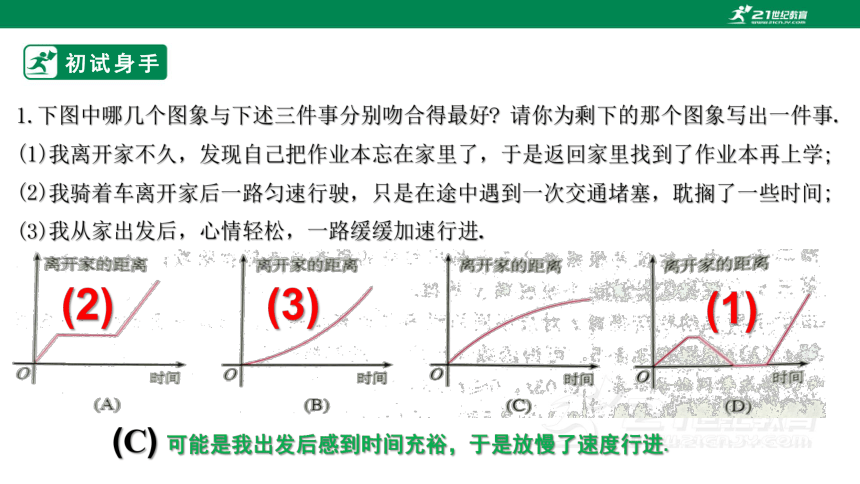
1.下图中哪几个图象与下述三件事分别吻合得最好 请你为剩下的那个图象写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车离开家后一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我从家出发后,心情轻松,一路缓缓加速行进.
(2)
(1)
(3)
(C) 可能是我出发后感到时间充裕,于是放慢了速度行进.
问题探究
【例8】依法纳税是每个公民应尽的义务,个人取得的所得应按照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:
个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②
问题探究
其中,“基本减除费用”(免征额)为每年60000元. 税率与速算扣除数见下表.
新知讲解
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象.
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
新知讲解
分析:该题的重要信息(2条公式和1张表)
个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②
新知讲解
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象.
分析:设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t).
计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①
税率与速算扣除数见表格
新知讲解
解:(1)根据上表,
可得函数y = f (t)的解析式为:
函数图象如图所示:
新知讲解
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
分析:个税税额根据应纳税所得额、税率和速算扣除数确定,
计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-
专项扣除-专项附加扣除-依法确定的其他扣除.②
其中,“基本减除费用”(免征额)为每年60000元. 税率与速算扣除数见下表.
新知讲解
(2)解:根据公式②,应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.小王全年应缴纳所得额为
t =189600-60000-189600× (8%+2%+1%+9%)-52800-4560
=0.8×189600-117360 = 34320(元).
将t 的值代入(1)中解析式的 y =0.03t,(0≤t≤36000).
得 y =0.03×34320=1029.6(元).
所以,小王应缴纳的综合所得个税税额为1029.6元.
该题请注意对实际背景的理解和分析, 以及分段函数概念的理解和应用.
新知讲解
综合所得收入额
应纳税所得额
应缴纳个税税额
公式②
y=f (t)
y=h (x)
综合所得收入额 应缴纳个税税额
189 600元 1029.6元
249 600元 5712元
初试身手
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5km以内(含5km),票价2元;
(2)5km以上,每增加5km,票价增加1元(不足5km的按5km计算).
如果某条线路的总里程为20km,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
解析:设票价为y 元,里程为x km,
由题意可知,自变量x 的取值范围是(0,20].
函数解析式为
据此画出函数图象:
新知讲解
【例9】 21世纪游乐园要建造一个直径为20m 的圆形喷水池,如图所示,计划在喷水池的周边靠近水面的位置安装一圈喷水头,使喷出的水柱在离池中心4m处达到最高,高度为6m。另外还要在喷水池的中心设计一个装饰物,使各方向喷来的水柱在此处汇合。这个装饰物的高度应当如何设计?
新知讲解
解:过水池的中心任意选取一个截面,如图所示.由物理学知识可知,喷出的水柱轨迹是抛物线型。建立如图所示的直角坐标系,由已知条件易知,水柱上任意一个点距中心的水平距离x(m)与此点的高度y(m)之间的函数关系是
新知讲解
于是,所求解析式是
注意:解应用题的步骤可以简单地概括为四个字:
设、列、解、答。
初试身手
3.如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为x,面积为y,把y表示成x 的函数。
25
解析:由条件知:
矩形的一边长为x,
则另一边长为
那么矩形的面积:
y=x
(025
x
新知讲解
【例10】(1)若x∈R,f(x)是y=2-x2,y=x这两个函数中的较小者,则f(x)的最大值为 ( )
A.2 B.1 C.-1 D.无最大值
(2)求函数y=|x+1|-|x-2|的最大值和最小值.
解:(1)选B 在同一坐标系中画出函数y=2-x2,y=x的图像,如图:
根据题意,图中实线部分即为函数f(x)的图像.
所以当x=1时,f(x)max=1.
新知讲解
(2)求函数y=|x+1|-|x-2|的最大值和最小值.
解:(2)y=|x+1|-|x-2|
=
作出函数的图像,由图可知,y∈[-3,3].所以函数的最大值为3,最小值为-3.
初试身手
4.函数f(x)在区间[-2,5]上的图像如图所示,则此函数的最小值、最大值分别是 ( )
A.-2,f(2) B.2,f(2)
C.-2,f(5) D.2,f(5)
解析:由函数的图像知,当x=-2时,有最小值-2;
当x=5时,有最大值f(5).故选C.
初试身手
课堂总结
1.理解函数的三种表示方法;
2.在具体的实际问题中能够选用恰当的表示法来表示函数;
3.利用函数模型解决实际问题时的方法步骤:
(1)对实际问题综合分析、归纳,抽象出函数模型种类;
(2)用相关的函数知识,进行合理设计,确定最佳解题方案,进行数学上的求解;
(3)对实际问题进行总结作答
作业布置
作业: p73 习题3.1 10,11.
补充题:
1.根据函数f(x)的图象写出它的解析式.
2.已知函数,
⑴画出函数f(x)的图像;
⑵求f(x)的定义域和值域.
3.某地区电力紧缺,电力公司为鼓励市民节约用电,
采用按月用电量分段收费的办法,若某户居民每月
应缴电费y(元)关于用电量x(度)函数图像是一条
折线(如图所示),根据图像求解下列问题:
⑴求y关于x的函数关系式;
⑵利用函数关系式,说明电力公司的收费标准;
⑶若该用户某月用电62度,则应缴电费多少元?若该用户某月缴电费105元,则该用户该月用电多少度?
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第三章
3.1.2函数的表示方法第2课时
人教A版(2019)
教学目标
学习目标 数学素养
1.明确函数的三种表示方法; 1.通过函数解析式,培养数学抽象素养;
2.在实际情境中,会根据不同需要选择恰当的方法表示函数; 2.利用函数图像培养数据分析素养;
3.通过具体实例,了解简单的分段函数,并能简单应用. 3.构建函数模型,培养数学建模素养.
知识回顾
1.函数的三种表示方法
表示法 定义
解析法 用___________表示两个变量之间的对应关系
图象法 用_________表示两个变量之间的对应关系
列表法 列出_________来表示两个变量之间的对应关系
数学表达式
图象
表格
温故知新
优点 缺点 联系
解 析 法 简明、全面地概括了变量间的对应关系;可以通过解析式求出任意自变量的值所对应的函数值. 形象性与直观性不足,变化趋势难判断,有些函数关系不能用解析式表示. 解析、列表和图象三种方法
各有优缺点,
面对实际问题时
根据需要恰当选择.
列 表 法 不需要计算就可以直接看出与自变量的值相对应的函数值. 只能列出部分自变量与函数的对应值,无法反映函数变化的全貌. 图 象 法 直观形象地表示随着自变量的变化,相应的函数值变化的趋势,有利于我们研究函数的某些性质. 只能近似得到数量关系,误差较大,容易误判断. 温故知新
2.分段函数
分段函数的定义域、值域分别是各段函数的定义域、值域的并集
(1)一般地,分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的 的函数.
(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是 .
(3)作分段函数图象时,应分别作出每一段的图象.
对应关系
并集
空集
新知形成
课前测评
1.函数f(x)=3x-1,x∈[1,5]的图象是( )
A.直线 B.射线 C.线段 D.离散的点
解析 ∵f(x)=3x-1为一次函数,图象为一条直线,而x∈[1,5],则此时图象为线段.故选C.
新知形成
课前测评
3.已知f(x)的图象如图,则f(x)的值域为________.
解析 由f(x)的图象知,f(x)的值域为[-4,3].
新知形成
【例7】下表3.1-4是某校高一(1)班三名同学在高一学年度
六次数学测试的成绩及班级平均分表.
请你对这三们同学在高一学年度的数学学习情况做一个分析.
第一次 第二次 第三次 第四次 第五次 第六次
王 伟 98 87 91 92 88 95
张 城 90 76 88 75 86 80
赵 磊 68 65 73 72 75 82
班平均分 88.2 78.3 85.4 80.3 75.7 82.6
新知讲解
解:从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将每位同学的“成绩”与“测试序号”之间的关系用函数图像(均为6个离散的点)表示出来,如下图,那么就能比较直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
新知讲解
从图可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
初试身手
1.下图中哪几个图象与下述三件事分别吻合得最好 请你为剩下的那个图象写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车离开家后一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我从家出发后,心情轻松,一路缓缓加速行进.
(2)
(1)
(3)
(C) 可能是我出发后感到时间充裕,于是放慢了速度行进.
问题探究
【例8】依法纳税是每个公民应尽的义务,个人取得的所得应按照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:
个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②
问题探究
其中,“基本减除费用”(免征额)为每年60000元. 税率与速算扣除数见下表.
新知讲解
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象.
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
新知讲解
分析:该题的重要信息(2条公式和1张表)
个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.②
新知讲解
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象.
分析:设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t).
计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①
税率与速算扣除数见表格
新知讲解
解:(1)根据上表,
可得函数y = f (t)的解析式为:
函数图象如图所示:
新知讲解
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
分析:个税税额根据应纳税所得额、税率和速算扣除数确定,
计算公式为:个税税额=应纳税所得额×税率-速算扣除数.①
应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-
专项扣除-专项附加扣除-依法确定的其他扣除.②
其中,“基本减除费用”(免征额)为每年60000元. 税率与速算扣除数见下表.
新知讲解
(2)解:根据公式②,应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.小王全年应缴纳所得额为
t =189600-60000-189600× (8%+2%+1%+9%)-52800-4560
=0.8×189600-117360 = 34320(元).
将t 的值代入(1)中解析式的 y =0.03t,(0≤t≤36000).
得 y =0.03×34320=1029.6(元).
所以,小王应缴纳的综合所得个税税额为1029.6元.
该题请注意对实际背景的理解和分析, 以及分段函数概念的理解和应用.
新知讲解
综合所得收入额
应纳税所得额
应缴纳个税税额
公式②
y=f (t)
y=h (x)
综合所得收入额 应缴纳个税税额
189 600元 1029.6元
249 600元 5712元
初试身手
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5km以内(含5km),票价2元;
(2)5km以上,每增加5km,票价增加1元(不足5km的按5km计算).
如果某条线路的总里程为20km,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
解析:设票价为y 元,里程为x km,
由题意可知,自变量x 的取值范围是(0,20].
函数解析式为
据此画出函数图象:
新知讲解
【例9】 21世纪游乐园要建造一个直径为20m 的圆形喷水池,如图所示,计划在喷水池的周边靠近水面的位置安装一圈喷水头,使喷出的水柱在离池中心4m处达到最高,高度为6m。另外还要在喷水池的中心设计一个装饰物,使各方向喷来的水柱在此处汇合。这个装饰物的高度应当如何设计?
新知讲解
解:过水池的中心任意选取一个截面,如图所示.由物理学知识可知,喷出的水柱轨迹是抛物线型。建立如图所示的直角坐标系,由已知条件易知,水柱上任意一个点距中心的水平距离x(m)与此点的高度y(m)之间的函数关系是
新知讲解
于是,所求解析式是
注意:解应用题的步骤可以简单地概括为四个字:
设、列、解、答。
初试身手
3.如图,把截面半径为25cm的圆形木头锯成矩形木料,如果矩形的一边长为x,面积为y,把y表示成x 的函数。
25
解析:由条件知:
矩形的一边长为x,
则另一边长为
那么矩形的面积:
y=x
(0
x
新知讲解
【例10】(1)若x∈R,f(x)是y=2-x2,y=x这两个函数中的较小者,则f(x)的最大值为 ( )
A.2 B.1 C.-1 D.无最大值
(2)求函数y=|x+1|-|x-2|的最大值和最小值.
解:(1)选B 在同一坐标系中画出函数y=2-x2,y=x的图像,如图:
根据题意,图中实线部分即为函数f(x)的图像.
所以当x=1时,f(x)max=1.
新知讲解
(2)求函数y=|x+1|-|x-2|的最大值和最小值.
解:(2)y=|x+1|-|x-2|
=
作出函数的图像,由图可知,y∈[-3,3].所以函数的最大值为3,最小值为-3.
初试身手
4.函数f(x)在区间[-2,5]上的图像如图所示,则此函数的最小值、最大值分别是 ( )
A.-2,f(2) B.2,f(2)
C.-2,f(5) D.2,f(5)
解析:由函数的图像知,当x=-2时,有最小值-2;
当x=5时,有最大值f(5).故选C.
初试身手
课堂总结
1.理解函数的三种表示方法;
2.在具体的实际问题中能够选用恰当的表示法来表示函数;
3.利用函数模型解决实际问题时的方法步骤:
(1)对实际问题综合分析、归纳,抽象出函数模型种类;
(2)用相关的函数知识,进行合理设计,确定最佳解题方案,进行数学上的求解;
(3)对实际问题进行总结作答
作业布置
作业: p73 习题3.1 10,11.
补充题:
1.根据函数f(x)的图象写出它的解析式.
2.已知函数,
⑴画出函数f(x)的图像;
⑵求f(x)的定义域和值域.
3.某地区电力紧缺,电力公司为鼓励市民节约用电,
采用按月用电量分段收费的办法,若某户居民每月
应缴电费y(元)关于用电量x(度)函数图像是一条
折线(如图所示),根据图像求解下列问题:
⑴求y关于x的函数关系式;
⑵利用函数关系式,说明电力公司的收费标准;
⑶若该用户某月用电62度,则应缴电费多少元?若该用户某月缴电费105元,则该用户该月用电多少度?
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
