垂直于弦的直径2[上学期]
文档属性
| 名称 | 垂直于弦的直径2[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 118.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-06 00:00:00 | ||
图片预览




文档简介
课件14张PPT。7.3垂直于弦的直径1.复习提问2.动手做实验3.问题探索4.应用举例5.习题训练6.课堂小结7.课后作业复习提问什么叫弦?什么叫弧? 答:连结圆上任意两点的线段
叫做弦。(如图中的线段AB)圆上任意两点间的部分叫
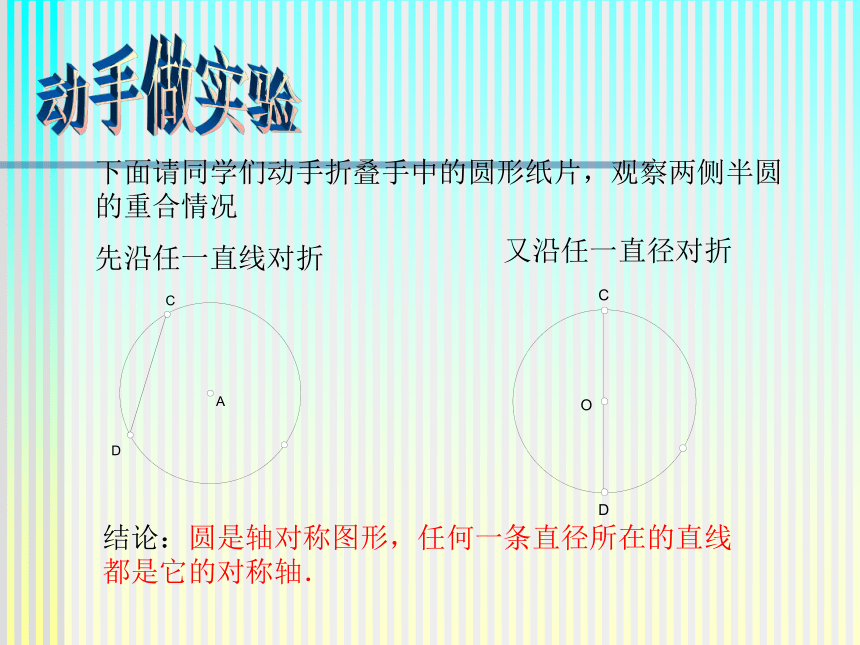
做圆弧 简称弧。其中 为优弧、 为劣弧(如图中的 、 )下面请同学们动手折叠手中的圆形纸片,观察两侧半圆
的重合情况 动手做实验先沿任一直线对折又沿任一直径对折结论:圆是轴对称图形,任何一条直径所在的直线
都是它的对称轴. 问题探索观察图形特点,发现两个图形中的直径都是互相平分的,
即AO=BO,CO=DO,所不同的是图(1)是斜交,图(2)是垂直. 图(1)当两条直径互相垂直时(图2),直径CD的两侧相邻的两条弧相等吗? 答:相等
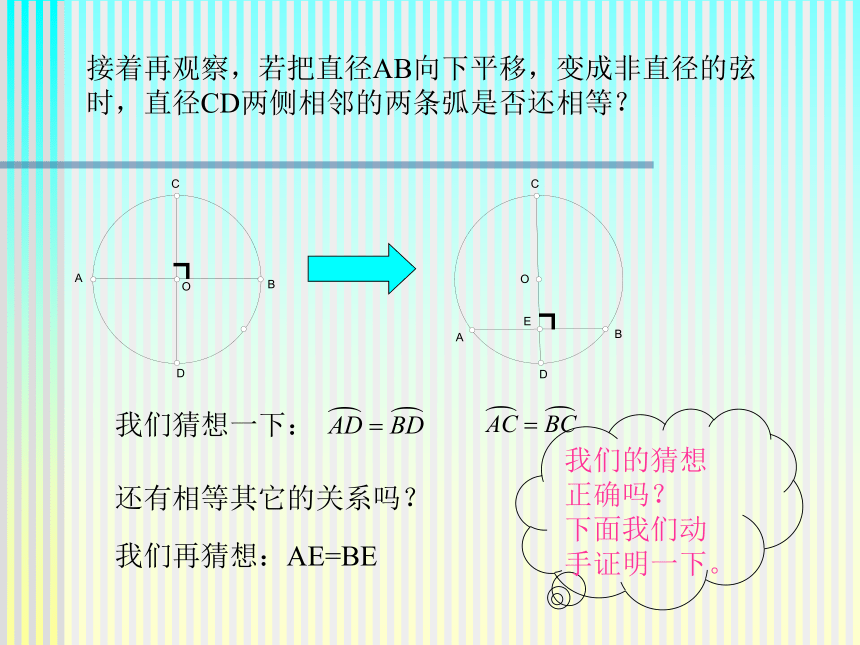
┓┓接着再观察,若把直径AB向下平移,变成非直径的弦
时,直径CD两侧相邻的两条弧是否还相等? 我们猜想一下:还有相等其它的关系吗? 我们再猜想:AE=BE我们的猜想正确吗?
下面我们动手证明一下。请同学们拿出刚才的圆形纸片如图画线、标点
我们知道OA=OB沿直径CD对折
我们发现CD两侧的两个半圆重合,
点A和点B重合,AE和BE重合,
、 分别和 、 重合∴AE=BE、 和 成立以上结论主要利用了圆的轴对称性来证明的,也是我们
这节课 要学习的一个定理垂径定理:垂直于弦的直径平分这条弦,并且平分弦
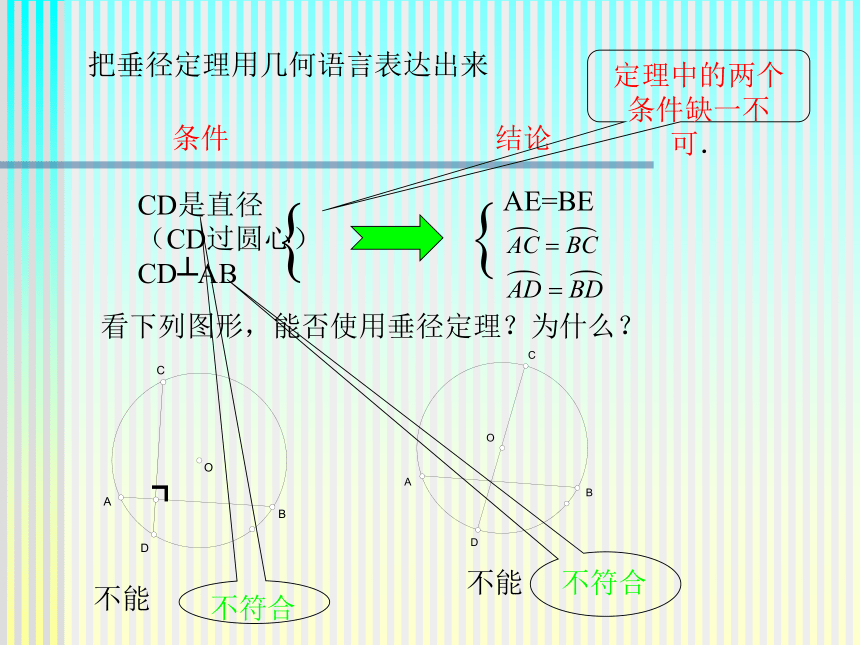
所对的两条弧. ┓把垂径定理用几何语言表达出来 条件CD是直径
(CD过圆心)
CD┴ABAE=BE结论看下列图形,能否使用垂径定理?为什么? ┓不能 不符合不能不符合定理中的两个条件缺一不可. 应用举例例1 如图7-26,已知在⊙O中,弦AB的长为8厘米,
圆心O到AB的距离为3厘米,求⊙O的半径. ┗E分析:由题设可作出OE⊥AB,垂足
为E,要求⊙O的半径,自然想到要连
结OA(或OB). 解:连结OA,过O作OE⊥AB,垂足为E
则OE=3cm, AE=BE∵AB=8cm∴ AE=4cm∴在RtΔAOE中,有=5(cm)∴ ⊙O的半径为5cm. 例2.已知:如图,在以O为圆心的两个同心圆中,大圆
的弦AB交小圆于C、D两点。
求正:AC=BD。E┓证明:过O作OE ⊥ AB,垂足为E则 AE=BE CE=DE∴ AE-CE=BE - DE即 AC=BD注意:在解有关弦的问题时,常常需要作“垂直于弦
的直径”作为辅助线。实际上,往往只须从圆
心作一条与弦垂直的线段,如例题中作的OE。习题训练1.在半径为50mm的⊙O中,有长50mm的弦。
计算:(1)点O与AB的距离;
(2)∠AOB的度数。解:根据题意 ,画出图形如图过O作OE⊥AB,垂足为E
连结OA、OB┓E则AE=BE=50/2=25(mm)在RtΔAOE中 (2) ∵ cos ∠AOE=∴∠AOE=300∴∠AOB=2 ∠AOE=600小结:有关弦的问题,常常过圆心作弦的垂线段后,
圆心到弦的距离、半径、弦长构成直角三角形,
便将问题转化为解直角三角形的问题. 课堂小结1.本节课我们主要学习了圆的轴对称性 和垂径定理垂径定理:垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧. 2.垂径定理的证明,是通过“实验—观察—猜想—证明”
实现的,体现了实践的观点、运动变化的观点和先猜想
后证明的观点,定理的引入还应用了从特殊到一般的思
想方法. 3.有关弦的问题,常常需要过圆心作弦的垂线段,这是
一条非常重要的辅助线.圆心到弦的距离、半径、弦长
构成直角三角形,便将问题转化为解直角三角形的问题. 课后作业习题7.1 A组 7. 12.下课谢谢指导
叫做弦。(如图中的线段AB)圆上任意两点间的部分叫
做圆弧 简称弧。其中 为优弧、 为劣弧(如图中的 、 )下面请同学们动手折叠手中的圆形纸片,观察两侧半圆
的重合情况 动手做实验先沿任一直线对折又沿任一直径对折结论:圆是轴对称图形,任何一条直径所在的直线
都是它的对称轴. 问题探索观察图形特点,发现两个图形中的直径都是互相平分的,
即AO=BO,CO=DO,所不同的是图(1)是斜交,图(2)是垂直. 图(1)当两条直径互相垂直时(图2),直径CD的两侧相邻的两条弧相等吗? 答:相等
┓┓接着再观察,若把直径AB向下平移,变成非直径的弦
时,直径CD两侧相邻的两条弧是否还相等? 我们猜想一下:还有相等其它的关系吗? 我们再猜想:AE=BE我们的猜想正确吗?
下面我们动手证明一下。请同学们拿出刚才的圆形纸片如图画线、标点
我们知道OA=OB沿直径CD对折
我们发现CD两侧的两个半圆重合,
点A和点B重合,AE和BE重合,
、 分别和 、 重合∴AE=BE、 和 成立以上结论主要利用了圆的轴对称性来证明的,也是我们
这节课 要学习的一个定理垂径定理:垂直于弦的直径平分这条弦,并且平分弦
所对的两条弧. ┓把垂径定理用几何语言表达出来 条件CD是直径
(CD过圆心)
CD┴ABAE=BE结论看下列图形,能否使用垂径定理?为什么? ┓不能 不符合不能不符合定理中的两个条件缺一不可. 应用举例例1 如图7-26,已知在⊙O中,弦AB的长为8厘米,
圆心O到AB的距离为3厘米,求⊙O的半径. ┗E分析:由题设可作出OE⊥AB,垂足
为E,要求⊙O的半径,自然想到要连
结OA(或OB). 解:连结OA,过O作OE⊥AB,垂足为E
则OE=3cm, AE=BE∵AB=8cm∴ AE=4cm∴在RtΔAOE中,有=5(cm)∴ ⊙O的半径为5cm. 例2.已知:如图,在以O为圆心的两个同心圆中,大圆
的弦AB交小圆于C、D两点。
求正:AC=BD。E┓证明:过O作OE ⊥ AB,垂足为E则 AE=BE CE=DE∴ AE-CE=BE - DE即 AC=BD注意:在解有关弦的问题时,常常需要作“垂直于弦
的直径”作为辅助线。实际上,往往只须从圆
心作一条与弦垂直的线段,如例题中作的OE。习题训练1.在半径为50mm的⊙O中,有长50mm的弦。
计算:(1)点O与AB的距离;
(2)∠AOB的度数。解:根据题意 ,画出图形如图过O作OE⊥AB,垂足为E
连结OA、OB┓E则AE=BE=50/2=25(mm)在RtΔAOE中 (2) ∵ cos ∠AOE=∴∠AOE=300∴∠AOB=2 ∠AOE=600小结:有关弦的问题,常常过圆心作弦的垂线段后,
圆心到弦的距离、半径、弦长构成直角三角形,
便将问题转化为解直角三角形的问题. 课堂小结1.本节课我们主要学习了圆的轴对称性 和垂径定理垂径定理:垂直于弦的直径平分这条弦,
并且平分弦所对的两条弧. 2.垂径定理的证明,是通过“实验—观察—猜想—证明”
实现的,体现了实践的观点、运动变化的观点和先猜想
后证明的观点,定理的引入还应用了从特殊到一般的思
想方法. 3.有关弦的问题,常常需要过圆心作弦的垂线段,这是
一条非常重要的辅助线.圆心到弦的距离、半径、弦长
构成直角三角形,便将问题转化为解直角三角形的问题. 课后作业习题7.1 A组 7. 12.下课谢谢指导
同课章节目录
