7.2 万有引力定律 课件 (共28张PPT)人教版(2019)必修第二册 第七章 万有引力与宇宙航行
文档属性
| 名称 | 7.2 万有引力定律 课件 (共28张PPT)人教版(2019)必修第二册 第七章 万有引力与宇宙航行 |  | |
| 格式 | pptx | ||
| 文件大小 | 20.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-08-07 18:02:09 | ||
图片预览




文档简介
(共28张PPT)
第2节 万有引力定律
必修
人教版必修第二册 第七章 万有引力与宇宙航行
知识回顾
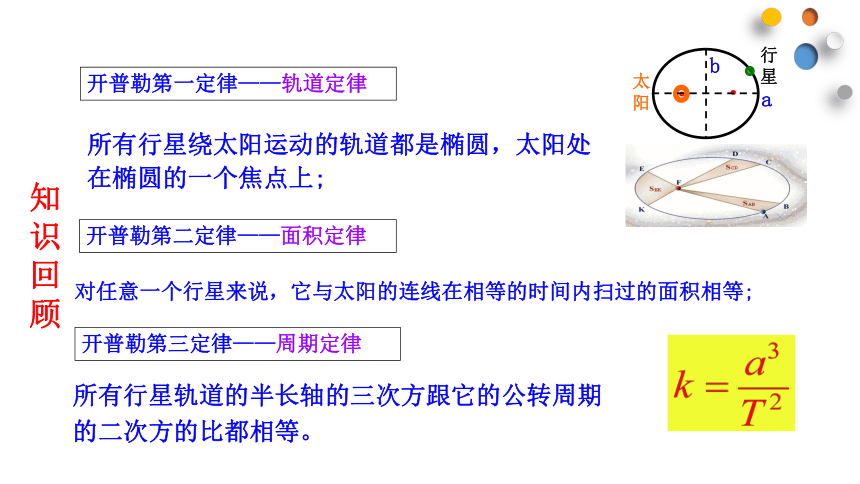
开普勒第一定律——轨道定律
所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上;
对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等;
开普勒第三定律——周期定律
所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等。
太阳
行星
b
a
开普勒第二定律——面积定律
更深入思考:是什么原因使行星绕太阳运动?
伽利略
行星的运动是受到了来自太阳的类似于磁力的作用,与距离成反比。
行星的运动是太阳吸引的缘故,并且力的大小与行星到太阳的距离的平方成反比。
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
开普勒
笛卡尔
胡克
一切物体都有合并的趋势。
历史的回顾
牛顿 (1643—1727)
英国著名的物理学家
当年牛顿在前人研究的基础上,凭借其超凡的数学能力和坚定的信念,不仅得出,使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力就是太阳对它的引力。还深入研究,最终发现了万有引力定律。
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远,那是因为我站在巨人的肩膀上。
历史的回顾
太阳
行星
a
简化
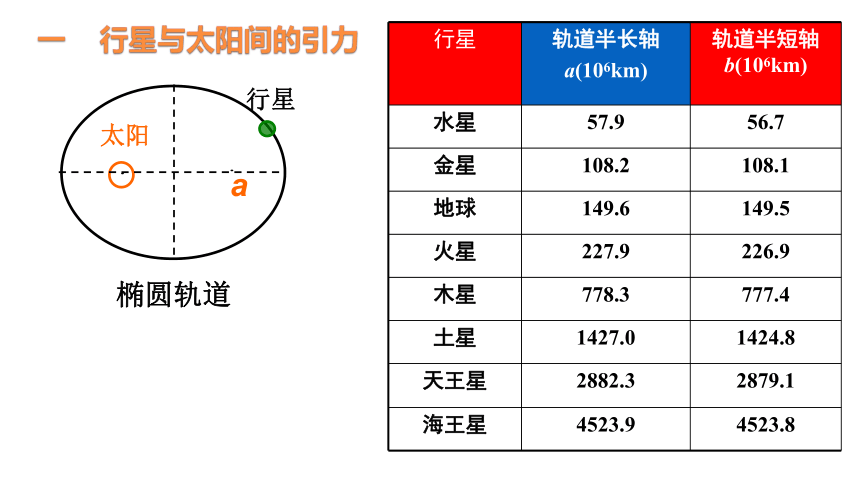
一 行星与太阳间的引力
行星 轨道半长轴 a(106km) 轨道半短轴b(106km)
水星 57.9 56.7
金星 108.2 108.1
地球 149.6 149.5
火星 227.9 226.9
木星 778.3 777.4
土星 1427.0 1424.8
天王星 2882.3 2879.1
海王星 4523.9 4523.8
椭圆轨道
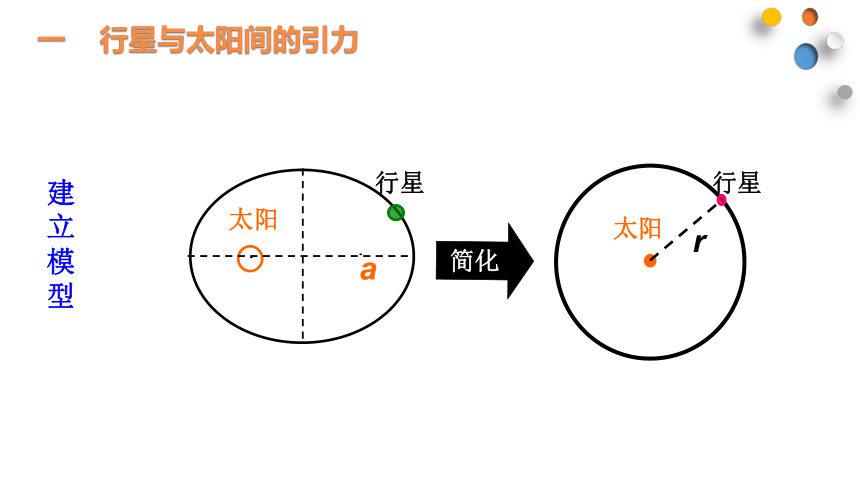
建立模型
太阳
行星
a
太阳
行星
r
一 行星与太阳间的引力
简化
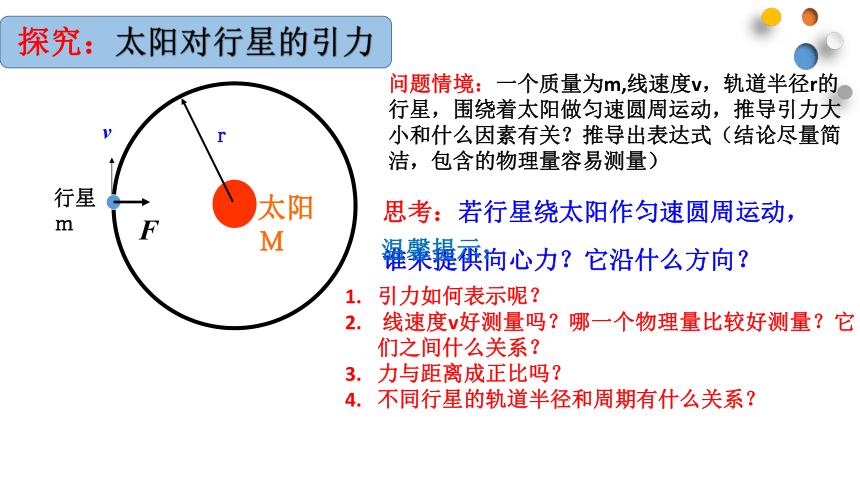
思考:若行星绕太阳作匀速圆周运动,谁来提供向心力?它沿什么方向?
F
太阳
M
行星
m
r
v
问题情境:一个质量为m,线速度v,轨道半径r的行星,围绕着太阳做匀速圆周运动,推导引力大小和什么因素有关?推导出表达式(结论尽量简洁,包含的物理量容易测量)
温馨提示:
引力如何表示呢?
线速度v好测量吗?哪一个物理量比较好测量?它们之间什么关系?
力与距离成正比吗?
不同行星的轨道半径和周期有什么关系?
探究:太阳对行星的引力
探究过程
太阳对行星的引力提供向心力
F=F ’
F’
’
猜想:
太阳对行星的引力
地球对月球的引力
地球对地面上苹果的引力
也许是同一种力,
遵从相同规律
内容:验证 地球对地面上苹果的引力
地球对月球的引力
遵循
思路:1、假定是同一种力,理论推导,得出结论
2、实际测量
若二者结果一致则假设成立
若二者结果不一致则假设不成立
二 月—地检验
二 月—地检验
已知量:
地球:重力加速度g = 9.8m/s2
半径R=6.4×106m
月球:与地球的距离r= 3.8×108m≈60R
公转周期 T =27.3天≈2.36×106s
根据已知量,请你设计方案,验证猜想的正确性。
二 月—地检验
问题1:假设地球对月球的作用力与太阳对行星的作用力是同一种力,其表达式是怎样的?
问题2:月球在这个力的作用下做什么运动?其向心加速度的表达式是怎样的?
问题4:苹果在这个力的作用下做什么运动?其加速度的表达式是怎样的?
问题3:假设地球对地面上的苹果的力也是同一种力,其表达式是怎样的?
小组合作探究
结论:月球绕地球运动的力以及地面物体所受地球的引力和太阳与行星之间的力遵循同一规律。
理论值与实际吻合!
实际测量
宇宙中的一切物体间都有引力:
大胆设想:
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小F与物体的质量m1和m2的乘积成正比,与它们的距离r的二次方成反比.
2.公式:
3.表达式中各物理量的含义及单位
三 万有引力定律
3、适用条件:只适用于两个质点间的引力。
a)、两个质点间的相互作用;
b)、可以看作质点的两个物体间的相互作用;
c)、若是两个均匀的球体,应是两球心间的距离.
m1
m2
r
若r→0,
F是否无穷大?
( 引力常量G=6.67×10-11
英国物理学家
卡文迪什
卡文迪什实验室
称量地球质量的实验室
N﹒m2/kg2 )
四 扭秤实验测定引力常量
1798年,英国物理学家卡文迪什巧妙地利用扭秤装置,
第一次在实验室里对两个铅球间的引力大小F做了精确测量
和计算,比较准确地测出了引力常量G的数值
r
F
r
F
m
m
m
m
引力常量G的测量实验
1798年,英国物理学家卡文迪什巧妙地利用扭秤装置,
第一次在实验室里对两个铅球间的引力大小F做了精确测量
和计算,比较准确地测出了引力常量G的数值
r
F
r
F
m
m
m
m
引力常量G的测量实验
两次放大及等效的思想
1.扭秤装置把微小力通过杠杆旋转明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标的移动来反映(二次放 大),从而确定物体间的万有引力。
巧妙之处:
实验数据:
G=6.67×10-11 N·m2/kg2
实验意义:
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
②开创了微小量测量的先河,使科学放大思想得到推广;
卡文迪什扭秤实验
③ 引力常量的普适性成为万有引力定律正确性的最早证据。
拓展视野
风云四号卫星质量约为5400 kg,地球质量约为6×1024 kg,两者相距3.6× 107 m,它们之间的引力多大?
约1670N
?
两个质量都为50kg的均匀球体,相距5m,它们之间的引力是多大?
6.67×10-9N(一粒芝麻重的几十万分之一!)
阿波罗8号从月球返航的途中,当地面控制中心问及“是谁在驾驶”的时候,指令长这样回答:“我想现在是牛顿在驾驶”。
最美地球照片——蓝色弹珠
课堂小结
科学规律发现的过程往往是大胆猜想和严格求证的结合
太阳与行星间的引力:
万有引力的猜想:
“天上”的力与“人间”的力是同一种力
万有引力的检验:
月---地检验
推广:
宇宙中一切物体间都有引力
万有引力定律的得出:
万有引力定律的检验:
引力常量G的测量实验
第2节 万有引力定律
必修
人教版必修第二册 第七章 万有引力与宇宙航行
知识回顾
开普勒第一定律——轨道定律
所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上;
对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等;
开普勒第三定律——周期定律
所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等。
太阳
行星
b
a
开普勒第二定律——面积定律
更深入思考:是什么原因使行星绕太阳运动?
伽利略
行星的运动是受到了来自太阳的类似于磁力的作用,与距离成反比。
行星的运动是太阳吸引的缘故,并且力的大小与行星到太阳的距离的平方成反比。
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
开普勒
笛卡尔
胡克
一切物体都有合并的趋势。
历史的回顾
牛顿 (1643—1727)
英国著名的物理学家
当年牛顿在前人研究的基础上,凭借其超凡的数学能力和坚定的信念,不仅得出,使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力就是太阳对它的引力。还深入研究,最终发现了万有引力定律。
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远,那是因为我站在巨人的肩膀上。
历史的回顾
太阳
行星
a
简化
一 行星与太阳间的引力
行星 轨道半长轴 a(106km) 轨道半短轴b(106km)
水星 57.9 56.7
金星 108.2 108.1
地球 149.6 149.5
火星 227.9 226.9
木星 778.3 777.4
土星 1427.0 1424.8
天王星 2882.3 2879.1
海王星 4523.9 4523.8
椭圆轨道
建立模型
太阳
行星
a
太阳
行星
r
一 行星与太阳间的引力
简化
思考:若行星绕太阳作匀速圆周运动,谁来提供向心力?它沿什么方向?
F
太阳
M
行星
m
r
v
问题情境:一个质量为m,线速度v,轨道半径r的行星,围绕着太阳做匀速圆周运动,推导引力大小和什么因素有关?推导出表达式(结论尽量简洁,包含的物理量容易测量)
温馨提示:
引力如何表示呢?
线速度v好测量吗?哪一个物理量比较好测量?它们之间什么关系?
力与距离成正比吗?
不同行星的轨道半径和周期有什么关系?
探究:太阳对行星的引力
探究过程
太阳对行星的引力提供向心力
F=F ’
F’
’
猜想:
太阳对行星的引力
地球对月球的引力
地球对地面上苹果的引力
也许是同一种力,
遵从相同规律
内容:验证 地球对地面上苹果的引力
地球对月球的引力
遵循
思路:1、假定是同一种力,理论推导,得出结论
2、实际测量
若二者结果一致则假设成立
若二者结果不一致则假设不成立
二 月—地检验
二 月—地检验
已知量:
地球:重力加速度g = 9.8m/s2
半径R=6.4×106m
月球:与地球的距离r= 3.8×108m≈60R
公转周期 T =27.3天≈2.36×106s
根据已知量,请你设计方案,验证猜想的正确性。
二 月—地检验
问题1:假设地球对月球的作用力与太阳对行星的作用力是同一种力,其表达式是怎样的?
问题2:月球在这个力的作用下做什么运动?其向心加速度的表达式是怎样的?
问题4:苹果在这个力的作用下做什么运动?其加速度的表达式是怎样的?
问题3:假设地球对地面上的苹果的力也是同一种力,其表达式是怎样的?
小组合作探究
结论:月球绕地球运动的力以及地面物体所受地球的引力和太阳与行星之间的力遵循同一规律。
理论值与实际吻合!
实际测量
宇宙中的一切物体间都有引力:
大胆设想:
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小F与物体的质量m1和m2的乘积成正比,与它们的距离r的二次方成反比.
2.公式:
3.表达式中各物理量的含义及单位
三 万有引力定律
3、适用条件:只适用于两个质点间的引力。
a)、两个质点间的相互作用;
b)、可以看作质点的两个物体间的相互作用;
c)、若是两个均匀的球体,应是两球心间的距离.
m1
m2
r
若r→0,
F是否无穷大?
( 引力常量G=6.67×10-11
英国物理学家
卡文迪什
卡文迪什实验室
称量地球质量的实验室
N﹒m2/kg2 )
四 扭秤实验测定引力常量
1798年,英国物理学家卡文迪什巧妙地利用扭秤装置,
第一次在实验室里对两个铅球间的引力大小F做了精确测量
和计算,比较准确地测出了引力常量G的数值
r
F
r
F
m
m
m
m
引力常量G的测量实验
1798年,英国物理学家卡文迪什巧妙地利用扭秤装置,
第一次在实验室里对两个铅球间的引力大小F做了精确测量
和计算,比较准确地测出了引力常量G的数值
r
F
r
F
m
m
m
m
引力常量G的测量实验
两次放大及等效的思想
1.扭秤装置把微小力通过杠杆旋转明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标的移动来反映(二次放 大),从而确定物体间的万有引力。
巧妙之处:
实验数据:
G=6.67×10-11 N·m2/kg2
实验意义:
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
②开创了微小量测量的先河,使科学放大思想得到推广;
卡文迪什扭秤实验
③ 引力常量的普适性成为万有引力定律正确性的最早证据。
拓展视野
风云四号卫星质量约为5400 kg,地球质量约为6×1024 kg,两者相距3.6× 107 m,它们之间的引力多大?
约1670N
?
两个质量都为50kg的均匀球体,相距5m,它们之间的引力是多大?
6.67×10-9N(一粒芝麻重的几十万分之一!)
阿波罗8号从月球返航的途中,当地面控制中心问及“是谁在驾驶”的时候,指令长这样回答:“我想现在是牛顿在驾驶”。
最美地球照片——蓝色弹珠
课堂小结
科学规律发现的过程往往是大胆猜想和严格求证的结合
太阳与行星间的引力:
万有引力的猜想:
“天上”的力与“人间”的力是同一种力
万有引力的检验:
月---地检验
推广:
宇宙中一切物体间都有引力
万有引力定律的得出:
万有引力定律的检验:
引力常量G的测量实验
