25.2 用列举法求概率(3)[上学期]
文档属性
| 名称 | 25.2 用列举法求概率(3)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 612.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-28 19:47:00 | ||
图片预览











文档简介
课件41张PPT。25.2 用列举法求概率(3)问题2.掷一颗普通的正方体骰子 求:
(1)”点数为1”的概率
(2)”点数为1或3”的概率
(3)”点数为偶数”的概率
(4)”点数大于2”的概率问题1.用列举法求事件A发生的概
率的条件是什么?P(点数为1)= P(点数为1或3)=
P(点数为偶数)= P(点数大于2)=3. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08"和“北京”的字块,如果婴儿能够排成"2008北京”或者“北京2008".则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.4.有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为( )。同时掷两枚硬币,求下列事件
的概率:(1)两枚硬币全部正面朝上;(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一
枚硬币反面朝上。准备题思考1、如果“同时掷两枚硬币”改为“把一
枚硬币掷两次”,所得到的结果有变化
吗?2、如果再把“把一枚硬币掷两次”改
为“把一枚硬币掷三次”,所得到的结
果又是什么?1.一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球.
(1)共有多少种不同的结果?
(2)摸出2个黑球有多种不同的结果?
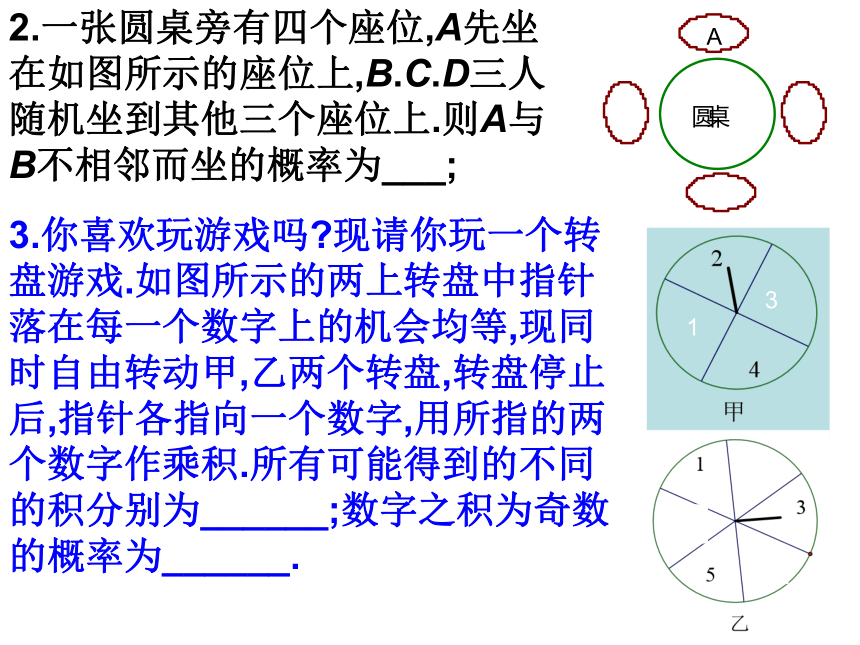
(3)摸出两个黑球的概率是多少?练一练2.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B.C.D三人随机坐到其他三个座位上.则A与B不相邻而坐的概率为___;3.你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两上转盘中指针落在每一个数字上的机会均等,现同时自由转动甲,乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.所有可能得到的不同的积分别为______;数字之积为奇数的概率为______.探究1同时掷两个质地均匀的骰子,计算下列
事件的概率:
(1)两个骰子的点数相同;
(2)两个骰子点数的和是9;
(3)至少有一个骰子的点数是2。分析:当一次试验要涉及两个因素(例如
掷两个骰子)并且可能出现的结果数目较
多时,为不重不漏地列出所有可能结果,
通常采用列表法。把两个骰子分别标记为第1个和第2个,列表如下:解:由表可看出,同时投掷两个骰子,可能
出现的结果有36个,它们出现的可能性相等。(1)满足两个骰子点数相同
(记为事件A)的结果有6个(2)满足两个骰子点数和为9
(记为事件B)的结果有4个(3)满足至少有一个骰子的点数为2(记
为事件C)的结果有11个。想一想: 如果把例5中的“同时掷两个骰子”改为
“把一个骰子掷两次”,所得的结果有变化
吗?没有变化这个游戏对小亮和小明公平吗?怎样才算公平 ?
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:”我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗? 思考1:你能求出小亮得分的概率吗?用表格表示总结经验:
当一次试验要涉及两个因素,并且可能出
现的结果数目较多时,为了不重不漏的列
出所有可能的结果,通常采用列表的办法解:由表中可以看出,在两堆牌中分别取一张,它可
能出现的结果有36个,它们出现的可能性相等
满足两张牌的数字之积为奇数(记为事件A)
的有(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)
这9种情况,所以
P(A)=
要“玩”出水平“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
真知灼见源于实践表格可以是:“配紫色”游戏游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)行家看“门道”例2 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.驶向胜利的彼岸用心领“悟”行家看“门道”学以致用解:每次游戏时,所有可能出现的结果如下:总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)1.在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,在随机地抽取一张。那么第二次取出的数字能够整除第一取出的数字的概率是多少?平心静气练一练小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少? 练习第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2(A1,A2)(A1,B1)(A1,B2)(A2,A1)(A2,B1)(A2,B2)(B1,A1)(B1,A2)(B1,B2)(B2,A1)(B2,A2)(B2,B1)用表格求所有可能结果时,你可要特别谨慎哦
例2:甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从3个口袋中各随机地抽取1个小球。
(1)取出的3个小球上恰好有1个、2个、和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验要涉及3个或更多的因素(例如
从3个口袋中取球)时,列方形表就不方便了,为
不重不漏地列出所有可能结果,通常采用树形图。解:根据题意,画出如下的“树形图”甲乙丙ABCDEHICDEHIHIHIHIHI从树形图看出,所有可能出现的结果共有12个A
C
HA
C
IA
D
HA
D
IA
E
HA
E
IB
C
HB
C
IB
D
HB
D
IB
E
HB
E
I(1)只有一个元音的字母的结果(红色)有5个有两个元音的字母的结果(绿色)有4个有三个元音的字母的结果(蓝色)有1个(2)全是辅音字母的结果(黑色)有2个用树状图和列表的方法求概率的前提:各种结果出现的可能性务必相同.例如注意:2.经过某十字路口的汽车,它可能继续直行,
也可能向左转或向右转,如果这三种可能性
大小相同。三辆汽车经过这个十字路口,求
下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左传。第
一
辆左右左右左直右第
二
辆第
三
辆直直左右直左右直左直右左直右左直右左直右左直右左直右左直右左直右共有27种行驶方向解:画树形图如下:(3)至少有两辆车向左传,有7种情况,即:左左左,左左直,左左右,左直左,
左右左,直左左,右左左。 数学病院用下图所示的转盘进行“配紫色”游戏,游戏者获胜的概率是多少?陈佳的思考过程如下:随机转动两个转盘,所有可能出现的结果如下:
你认为她的想法对吗,为什么?总共有9种结果,每种结果出现的可能性相同,而能够 配成紫色的结果只有一种: (红,蓝),故游戏者获胜的概率为1∕9 。用树状图或列表法求概率时,各种结果出现的可能性务必相同。(2006年广东茂名市第18题改编)如图是配紫游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?A盘 B盘 商店实行有奖销售,印有1000张彩券. 其中有5张一等奖,15张二等奖,30张三等奖,其余均无奖,任意抽一张,则获奖的概率是多少?(2006年广东茂名市第18题改编)如图是配紫游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?A盘 B盘一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?O√一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?O一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?O评价试卷原题一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.要学会建立适当的数学模型小结:用树状图和列表各自的优缺点及局限性.有放回还是无放回的问题同学们再见8、有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为( )。9、某组16名学生,其中男女生各一半,把全组学生分成人数相等的两个小组,则分得每小组里男、女人数相同的概率是( )10一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球.
(1)共有多少种不同的结果?
(2)摸出2个黑球有多种不同的结果?
(3)摸出两个黑球的概率是多少?
(1)”点数为1”的概率
(2)”点数为1或3”的概率
(3)”点数为偶数”的概率
(4)”点数大于2”的概率问题1.用列举法求事件A发生的概
率的条件是什么?P(点数为1)= P(点数为1或3)=
P(点数为偶数)= P(点数大于2)=3. 有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08"和“北京”的字块,如果婴儿能够排成"2008北京”或者“北京2008".则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.4.有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为( )。同时掷两枚硬币,求下列事件
的概率:(1)两枚硬币全部正面朝上;(2)两枚硬币全部反面朝上;
(3)一枚硬币正面朝上,一
枚硬币反面朝上。准备题思考1、如果“同时掷两枚硬币”改为“把一
枚硬币掷两次”,所得到的结果有变化
吗?2、如果再把“把一枚硬币掷两次”改
为“把一枚硬币掷三次”,所得到的结
果又是什么?1.一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球.
(1)共有多少种不同的结果?
(2)摸出2个黑球有多种不同的结果?
(3)摸出两个黑球的概率是多少?练一练2.一张圆桌旁有四个座位,A先坐在如图所示的座位上,B.C.D三人随机坐到其他三个座位上.则A与B不相邻而坐的概率为___;3.你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两上转盘中指针落在每一个数字上的机会均等,现同时自由转动甲,乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.所有可能得到的不同的积分别为______;数字之积为奇数的概率为______.探究1同时掷两个质地均匀的骰子,计算下列
事件的概率:
(1)两个骰子的点数相同;
(2)两个骰子点数的和是9;
(3)至少有一个骰子的点数是2。分析:当一次试验要涉及两个因素(例如
掷两个骰子)并且可能出现的结果数目较
多时,为不重不漏地列出所有可能结果,
通常采用列表法。把两个骰子分别标记为第1个和第2个,列表如下:解:由表可看出,同时投掷两个骰子,可能
出现的结果有36个,它们出现的可能性相等。(1)满足两个骰子点数相同
(记为事件A)的结果有6个(2)满足两个骰子点数和为9
(记为事件B)的结果有4个(3)满足至少有一个骰子的点数为2(记
为事件C)的结果有11个。想一想: 如果把例5中的“同时掷两个骰子”改为
“把一个骰子掷两次”,所得的结果有变化
吗?没有变化这个游戏对小亮和小明公平吗?怎样才算公平 ?
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:”我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。如果你是小亮,你愿意接受这个游戏的规则吗? 思考1:你能求出小亮得分的概率吗?用表格表示总结经验:
当一次试验要涉及两个因素,并且可能出
现的结果数目较多时,为了不重不漏的列
出所有可能的结果,通常采用列表的办法解:由表中可以看出,在两堆牌中分别取一张,它可
能出现的结果有36个,它们出现的可能性相等
满足两张牌的数字之积为奇数(记为事件A)
的有(1,1)(1,3)(1,5)(3,1)(3,3)(3,5)(5,1)(5,3)(5,5)
这9种情况,所以
P(A)=
要“玩”出水平“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
真知灼见源于实践表格可以是:“配紫色”游戏游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)行家看“门道”例2 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.驶向胜利的彼岸用心领“悟”行家看“门道”学以致用解:每次游戏时,所有可能出现的结果如下:总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)1.在6张卡片上分别写有1~6的整数,随机地抽取一张后放回,在随机地抽取一张。那么第二次取出的数字能够整除第一取出的数字的概率是多少?平心静气练一练小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少? 练习第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2(A1,A2)(A1,B1)(A1,B2)(A2,A1)(A2,B1)(A2,B2)(B1,A1)(B1,A2)(B1,B2)(B2,A1)(B2,A2)(B2,B1)用表格求所有可能结果时,你可要特别谨慎哦
例2:甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C、D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从3个口袋中各随机地抽取1个小球。
(1)取出的3个小球上恰好有1个、2个、和3个元音字母的概率分别是多少?
(2)取出的3个小球上全是辅音字母的概率是多少?
分析:当一次试验要涉及3个或更多的因素(例如
从3个口袋中取球)时,列方形表就不方便了,为
不重不漏地列出所有可能结果,通常采用树形图。解:根据题意,画出如下的“树形图”甲乙丙ABCDEHICDEHIHIHIHIHI从树形图看出,所有可能出现的结果共有12个A
C
HA
C
IA
D
HA
D
IA
E
HA
E
IB
C
HB
C
IB
D
HB
D
IB
E
HB
E
I(1)只有一个元音的字母的结果(红色)有5个有两个元音的字母的结果(绿色)有4个有三个元音的字母的结果(蓝色)有1个(2)全是辅音字母的结果(黑色)有2个用树状图和列表的方法求概率的前提:各种结果出现的可能性务必相同.例如注意:2.经过某十字路口的汽车,它可能继续直行,
也可能向左转或向右转,如果这三种可能性
大小相同。三辆汽车经过这个十字路口,求
下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左传。第
一
辆左右左右左直右第
二
辆第
三
辆直直左右直左右直左直右左直右左直右左直右左直右左直右左直右左直右共有27种行驶方向解:画树形图如下:(3)至少有两辆车向左传,有7种情况,即:左左左,左左直,左左右,左直左,
左右左,直左左,右左左。 数学病院用下图所示的转盘进行“配紫色”游戏,游戏者获胜的概率是多少?陈佳的思考过程如下:随机转动两个转盘,所有可能出现的结果如下:
你认为她的想法对吗,为什么?总共有9种结果,每种结果出现的可能性相同,而能够 配成紫色的结果只有一种: (红,蓝),故游戏者获胜的概率为1∕9 。用树状图或列表法求概率时,各种结果出现的可能性务必相同。(2006年广东茂名市第18题改编)如图是配紫游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?A盘 B盘 商店实行有奖销售,印有1000张彩券. 其中有5张一等奖,15张二等奖,30张三等奖,其余均无奖,任意抽一张,则获奖的概率是多少?(2006年广东茂名市第18题改编)如图是配紫游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?A盘 B盘一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?O√一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?O一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?O评价试卷原题一只位于O点的蚂蚁在如图所示的树枝上往前寻觅粮食(假设带箭头的树枝上有粮食), 已知蚂蚁在每个岔路口都会随机地选择一条路径,问它获得粮食的概率是多少?从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.要学会建立适当的数学模型小结:用树状图和列表各自的优缺点及局限性.有放回还是无放回的问题同学们再见8、有100张卡片(从1号到100号),从中任取1张,取到的卡号是7的倍数的概率为( )。9、某组16名学生,其中男女生各一半,把全组学生分成人数相等的两个小组,则分得每小组里男、女人数相同的概率是( )10一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球.
(1)共有多少种不同的结果?
(2)摸出2个黑球有多种不同的结果?
(3)摸出两个黑球的概率是多少?
同课章节目录
