第三章不等式 复习课讲义(含答案)
文档属性
| 名称 | 第三章不等式 复习课讲义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 809.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 19:04:27 | ||
图片预览



文档简介
编号:017 课题: §3 不等式复习课
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、理解并掌握不等式基本性质.
2、理解并掌握基本不等式及其应用.
3、会求解与一元二次不等式有关的综合问题.
本节重点难点
重点:基本不等式及其应用;
难点:求解与一元二次不等式有关的综合问题.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
构建网络结构简图
1. 实数比较大小的基本事实
文字语言 符号表示
如果a>b,那么a-b是______; 如果a<b,那么a-b是______; 如果a=b,那么a-b等于______ a>b a-b____0 a<b a-b____0 a=b a-b____0
2.不等式的基本性质
别名 性质内容 注意
性质1 对称性 a>b b____a 可逆
性质2 传递性 a>b,b>c ____ 同向
性质3 可加性 a>b ________ 可逆
性质3 的推论 移项 法则 a+b>c a____c-b 可逆
性质4 可乘性 a>b,c>0 ac____bc a>b,c<0 _____ c的 符号
性质5 同向可加性 a>b,c>d ______ 同向
性质6 同向同 正可乘性 a>b>0,c>d>0 ______ 同向 同正
3. 算术平均数与几何平均数
对于正数a,b,我们把__________称为a,b的算术平均数,________称为a,b的几何平均数.
4.基本不等式
(1)公式:
①条件:a,b是正数;
②结论:___________________;
③等号成立:当且仅当a=b时.
(2)本质:基本不等式表明,两个正数的算术平均数不小于它们的几何平均数.
(3)变形式:当a,b∈R时,a2+b2____2ab,a2+b2+2ab______4ab,ab _____,
Ab____(当且仅当a=b时,等号成立).
5.用基本不等式求最值的结论
对于正数a,b,
(1)和a+b为定值时,积ab有最____值;积ab为定值时,和a+b有最____值.
(2)取等号的条件:当且仅当________时,=.
(3)应用:求和式的最小值,乘积式的最大值.
6. 二次函数的零点
一般地,一元二次方程的根就是二次函数当函数值取零时____________,即二次函数的图象与_______________,也称为二次函数的零点.
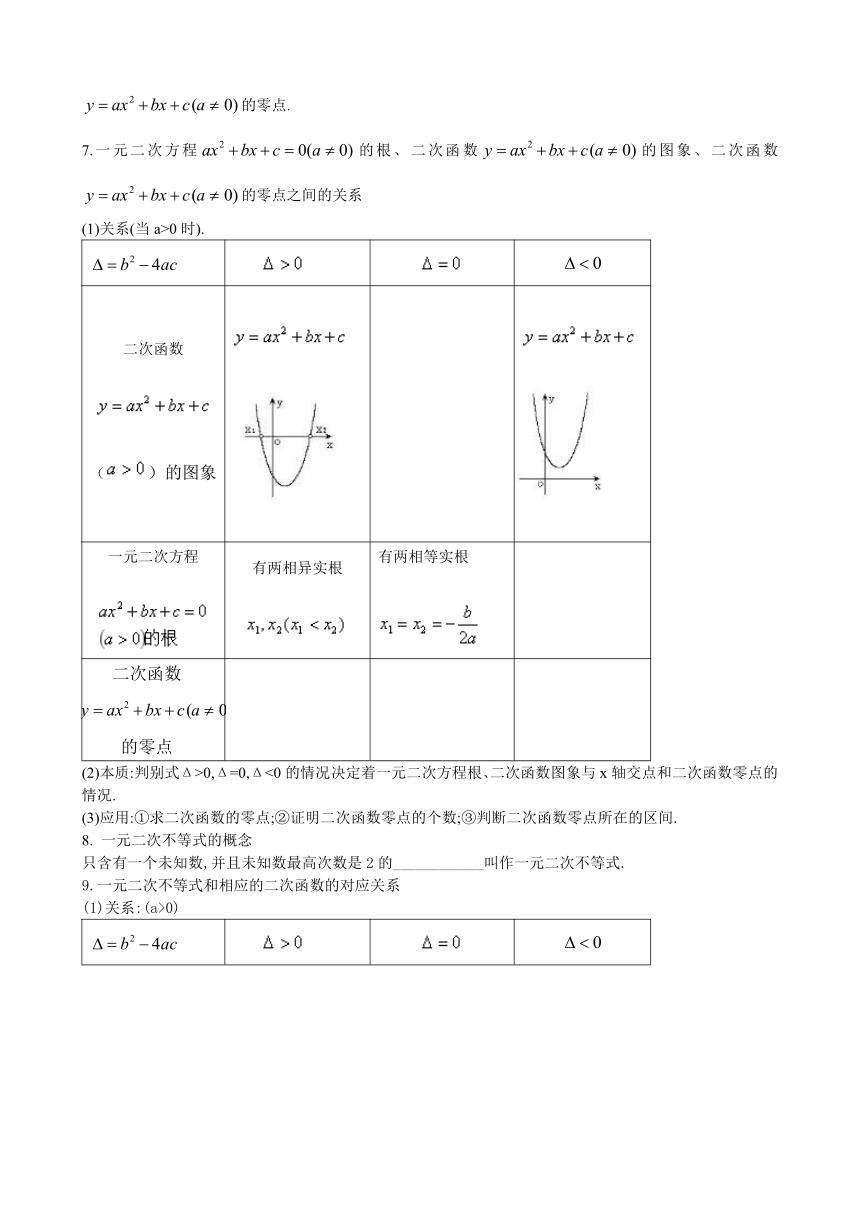
7.一元二次方程的根、二次函数的图象、二次函数的零点之间的关系
(1)关系(当a>0时).
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根
二次函数的零点
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
8. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的____________叫作一元二次不等式.
9.一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
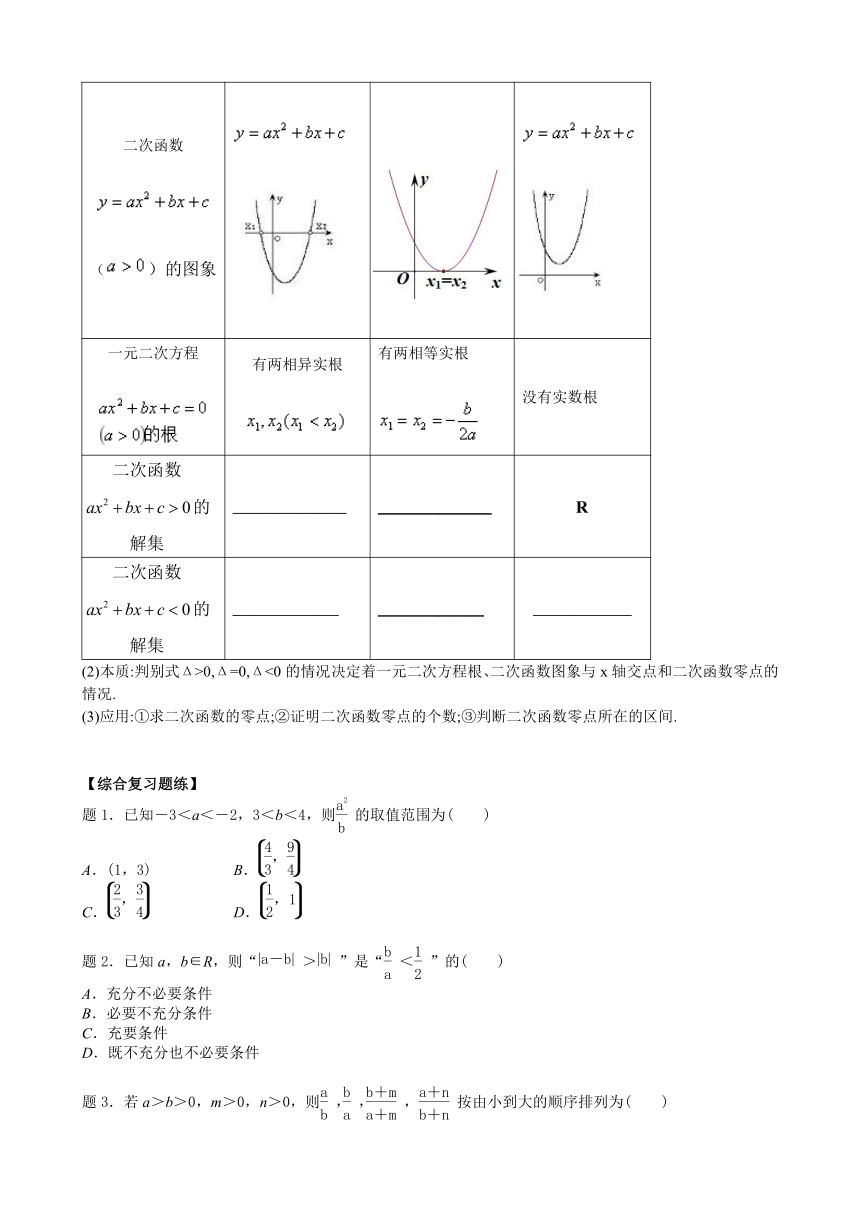
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集 _______________ _______________
二次函数的解集 ______________ ______________ _____________
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【综合复习题练】
题1.已知-3<a<-2,3<b<4,则的取值范围为( )
A.(1,3) B.
C. D.
题2.已知a,b∈R,则“>”是“<”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
题3.若a>b>0,m>0,n>0,则,,,按由小到大的顺序排列为( )
A.<<<
B.<<<
C.<<<
D.<<<
题4.若两个正实数x,y满足4x+y=xy且存在这样的x,y使不等式x+<m2+3m有解,则实数m的取值范围是( )
A.(-1,4)
B.(-4,1)
C.(-∞,-4)∪(1,+∞)
D.(-∞,-3)∪(0,+∞)
题5.设x>0,y>0,且=,则当x+取最小值时,x2+=( )
A.12 B.8 C.16 D.
题6.已知a,b∈R且ab≠0,若对任意的x≤0均有(x-a)(x-b)(x-2a-b)≤0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
题7.已知0<a<1,0<b<1,且4(a+b)=4ab+3,则a+2b的最大值为( )
A.2 B.2
C.3- D.3-2
题8.若实数x,y,z满足,记P=xy+yz+xz+y2,Q=x+2y+z,则P与Q的大小关系是( )
A.P<Q B.P>Q
C.P=Q D.不确定
题9(多选题).下列结论不正确的是( )
A.<<0 |a|>|b|
B.> a>b
C. <
D. <
题10(多选题).周长为3+2的直角三角形的面积可能为( )
A.3 B.3
C. D.
题11(多选题).已知不等式x2+ax+b>0(a>0)的解集是{x|x≠d},则下列四个结论中正确的是( )
A.a2=4b
B.a2+≥4
C.若不等式x2+ax-b<0的解集为(x1,x2),则x1x2>0
D.若不等式x2+ax+b<c的解集为(x1,x2),且|x1-x2|=4,则c=4
题12(多选题).下列关于一元二次不等式叙述正确的是( )
A.若一元二次不等式ax2+bx+c>0的解集为 ,则a<0,且Δ≤0
B.若==,则一元二次不等式a1x2+b1x+c1>0的解集与一元二次不等式a2x2+b2x+c2>0的解集相等
C.已知a∈Z,关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则所有符合条件的a的值之和是22
D.若一元二次不等式ax2+bx+c≥0的解集为R,且b>a,则的最小值为3
题13.若-10<a<b<8,则a+b的取值范围是__________;+b的取值范围是__________.
题14.已知正实数a,b满足a+b=1,则+的最小值是__________.
题15.若正实数x,y满足x++y+=10,则-的最大值是__________.
题16.若A=(-2,5),则以A为解集的一个一元二次不等式可以是__________.
题17.某种商品计划提价,现有四种方案:
方案(1)先提价m%,再提价n%;
方案(2)先提价n%,再提价m%;
方案(3)分两次提价,每次提价%;
方案(4)一次性提价(m+n)%.
已知m>n>0,那么四种提价方案中,提价最多的是哪种方案?
题18.若a,b,c都是正数,求证:a2+b2+c2≥++.
题19.设二次函数y=ax2+bx+c(a≠0).
(1)若b=2,c=-1且二次函数的最大值为正数,求a的取值范围.
(2)若ax2-x-2<0的解集是,求y>c2的解集.
(3)设二次函数y=ax2+bx+c(a>0)的两个零点分别为x1,x2,满足0<x1<x2<,证明:当x∈(0,x1)时,0<y<x1-x.
题20.中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为3 m,底面积为12 m2,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体的报价为每平方米150元,屋顶和地面以及其他报价共计7 200元,设屋子的左右两面墙的长度均为x m(2≤x≤6).
(1)当左右两面墙的长度为多少米时,甲工程队的报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(a>0);若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,求a的取值范围.
编号:017 课题: §3 不等式复习课
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、理解并掌握不等式基本性质.
2、理解并掌握基本不等式及其应用.
3、会求解与一元二次不等式有关的综合问题.
本节重点难点
重点:基本不等式及其应用;
难点:求解与一元二次不等式有关的综合问题.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
构建网络结构简图
1. 实数比较大小的基本事实
文字语言 符号表示
如果a>b,那么a-b是_正数_; 如果a<b,那么a-b是_负数_; 如果a=b,那么a-b等于_0_ a>b a-b_>_0 a<b a-b_<_0 a=b a-b_=_0
2.不等式的基本性质
别名 性质内容 注意
性质1 对称性 a>b b < a 可逆
性质2 传递性 a>b,b>c a>c 同向
性质3 可加性 a>b a+c>b+c 可逆
性质3 的推论 移项 法则 a+b>c a > c-b 可逆
性质4 可乘性 a>b,c>0 ac > bc a>b,c<0 ac性质5 同向可加性 a>b,c>d a+c>b+d 同向
性质6 同向同 正可乘性 a>b>0,c>d>0 ac>bd 同向 同正
3. 算术平均数与几何平均数
对于正数a,b,我们把 称为a,b的算术平均数, 称为a,b的几何平均数.
4.基本不等式
(1)公式:
①条件:a,b是正数;
②结论: ;
③等号成立:当且仅当a=b时.
(2)本质:基本不等式表明,两个正数的算术平均数不小于它们的几何平均数.
(3)变形式:当a,b∈R时,a2+b2 ≥ 2ab,a2+b2+2ab ≥ 4ab,ab ≤ ,
ab ≤ (当且仅当a=b时,等号成立).
5.用基本不等式求最值的结论
对于正数a,b,
(1)和a+b为定值时,积ab有最 大 值;积ab为定值时,和a+b有最 小 值.
(2)取等号的条件:当且仅当 a=b 时, .
(3)应用:求和式的最小值,乘积式的最大值.
6. 二次函数的零点
一般地,一元二次方程的根就是二次函数当函数值取零时_自变量的值_,即二次函数的图象与__轴交点的横坐标____,也称为二次函数的零点.
7.一元二次方程的根、二次函数的图象、二次函数的零点之间的关系
(1)关系(当a>0时).
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的零点 有两个零点 有一个零点 无零点
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
8. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的_整式不等式_叫作一元二次不等式.
9.一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集
二次函数的解集
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【综合复习题练】
题1.已知-3<a<-2,3<b<4,则的取值范围为( )
A.(1,3) B.
C. D.
【解析】选A.因为-3<a<-2,所以a2∈(4,9),而3<b<4,所以<<,故的取值范围为(1,3).
题2.已知a,b∈R,则“>”是“<”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【解析】选C.由>得a2+b2-2ab>b2,所以a(a-2b)>0,
所以>0,所以1->0,所以<.反之,也成立.
所以“>”是“<”的充要条件.
题3.若a>b>0,m>0,n>0,则,,,按由小到大的顺序排列为( )
A.<<<
B.<<<
C.<<<
D.<<<
【解析】选A.-==,
因为a>b>0,m>0,所以<0,所以<,-
=
=,
因为a>b>0,m>0,n>0,
所以<0,
所以<,-==,
因为a>b>0,n>0,所以<0,所以<,所以<<<.
题4.若两个正实数x,y满足4x+y=xy且存在这样的x,y使不等式x+<m2+3m有解,则实数m的取值范围是( )
A.(-1,4)
B.(-4,1)
C.(-∞,-4)∪(1,+∞)
D.(-∞,-3)∪(0,+∞)
【解析】选C.由4x+y=xy +=1知,
=1+++1≥2+2=4,当且仅当x=2,y=8时,等号成立,则使不等式x+<m2+3m有解,只需满足m2+3m>4即可,解得m的取值范围是(-∞,-4)∪(1,+∞).
题5.设x>0,y>0,且=,则当x+取最小值时,x2+=( )
A.12 B.8 C.16 D.
【解析】选A.因为x>0,y>0,所以当x+取最小值时,取最小值,
因为=x2++,=,所以x2+=+,
所以=+≥2=16,
所以x+≥4,当且仅当=,即x=2y时取等号,
所以x2++=16,所以x2++=16,
所以x2+=16-=12.
题6.已知a,b∈R且ab≠0,若对任意的x≤0均有(x-a)(x-b)(x-2a-b)≤0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
【解析】选D.因为ab≠0,所以b≠ab+b,若对任意的x≤0均有(x-a)(x-b)(x-2a-b)≤0,则ab(2a+b)≥0,
所以a,b不可能同时为负,至少有一个为正,
①若a>0,b>0,显然成立;
②若a>0,b<0,则2a+b≤0,此时要使(x-a)(x-b)(x-2a-b)≤0在(-∞,0]上恒成立,则必有b=2a+b,则a=0,矛盾;
③若a<0,b>0,则2a+b≤0,此时要使(x-a)(x-b)(x-2a-b)≤0在(-∞,0]上恒成立,则必有a=2a+b,则a+b=0,符合题意;
综上,b>0.
题7.已知0<a<1,0<b<1,且4(a+b)=4ab+3,则a+2b的最大值为( )
A.2 B.2
C.3- D.3-2
【解析】选C.因为4(a+b)=4ab+3,所以4ab-4a-4b+3=0,
所以4ab-4a-4b+4=1,即ab-a-b+1=,
即(1-a)(1-b)=.令x=1-a>0,y=1-b>0,则a=1-x,b=1-y,y=,
所以a+2b=1-x+2(1-y)=-x-2y+3=-x-+3
=-(x+)+3≤-2+3
=3-(当且仅当x=,即x=时,等号成立).
故a+2b的最大值为3-.
题8.若实数x,y,z满足,记P=xy+yz+xz+y2,Q=x+2y+z,则P与Q的大小关系是( )
A.P<Q B.P>Q
C.P=Q D.不确定
【解析】选A.P-Q=xy+yz+xz+y2-(x+2y+z)=xz+(y-1)(x+z)+(y-1)2-1=(x+y-1)(z+y-1)-1,
因为,所以x+y-1∈(0,1),z+y-1∈(0,1),
所以(x+y-1)(z+y-1)∈(0,1),
所以P-Q<1-1=0,即P<Q.
题9(多选题).下列结论不正确的是( )
A.<<0 |a|>|b|
B.> a>b
C. <
D. <
【解析】选ABD.A:因为<<0,所以ab>0且->->0,
因此-·ab>-·ab>0·ab,
即-b>-a>0 >>0 >,故A不正确,符合题意;
B:因为>,显然4>8不成立,所以B不正确,符合题意;
C:由a3>b3 a3-b3=(a-b)(a2+ab+b2)>0,而ab>0,
所以有a>b,而-=<0 <,故C正确,不符合题意;
D:若a=-2,b=-1,显然成立,但是<不成立,故D不正确,符合题意.
题10(多选题).周长为3+2的直角三角形的面积可能为( )
A.3 B.3
C. D.
【解析】选CD.设直角三角形的三边分别为a,b,c且c为斜边,
所以a+b+c=3+2 a+b+=3+2 3+2≥2+ ab≤,而直角三角形的面积S=≤,当且仅当a=b时等号成立,而a=b时,可得,
所以0<S≤.所以C,D满足题意.
题11(多选题).已知不等式x2+ax+b>0(a>0)的解集是{x|x≠d},则下列四个结论中正确的是( )
A.a2=4b
B.a2+≥4
C.若不等式x2+ax-b<0的解集为(x1,x2),则x1x2>0
D.若不等式x2+ax+b<c的解集为(x1,x2),且|x1-x2|=4,则c=4
【解析】选ABD.由题意得Δ=a2-4b=0,所以a2=4b,所以A正确;
对于B:a2+=a2+≥2=4,当且仅当a2=,即a=时等号成立,所以B正确;
对于C:由根与系数的关系,知x1x2=-b=-<0,所以C错误;
对于D:由根与系数的关系,知x1+x2=-a,x1x2=b-c=-c,
则|x1-x2|===2=4,解得c=4,所以D正确.
题12(多选题).下列关于一元二次不等式叙述正确的是( )
A.若一元二次不等式ax2+bx+c>0的解集为 ,则a<0,且Δ≤0
B.若==,则一元二次不等式a1x2+b1x+c1>0的解集与一元二次不等式a2x2+b2x+c2>0的解集相等
C.已知a∈Z,关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则所有符合条件的a的值之和是22
D.若一元二次不等式ax2+bx+c≥0的解集为R,且b>a,则的最小值为3
【解析】选AD.对A,若一元二次不等式ax2+bx+c>0的解集为 ,
则ax2+bx+c≤0恒成立,所以a<0,且Δ≤0,故A正确;
对B,若a1和a2的符号相反,则两个一元二次不等式解集不同,故B错误;
对C,设f(x)=x2-6x+a=(x-3)2+a-9,
有,解得5<a≤8,由a∈Z,知a=6,7,8,和为21,故C错误;
对D,则有a>0,Δ=b2-4ac=0,所以b>a>0,
令t=,则t>1,t-1>0,
=====++≥2+=3,
当且仅当=,即t=4时取等号,故D正确.
题13.若-10<a<b<8,则a+b的取值范围是__________;+b的取值范围是__________.
【解析】当a≥0时,0≤a<8,0<b<8,故0<a+b<16,
而+b=a+b,所以0<+b<16;
当a<0时,-10<a<0,故0<=-a<10,
又-10<b<8,所以-20<a+b<8,-10<+b<18,
又a<b,所以+b>0,所以0<+b<18.
综上,a+b的取值范围是(-20,16),+b的取值范围是(0,18).
答案:(-20,16) (0,18)
题14.已知正实数a,b满足a+b=1,则+的最小值是__________.
【解析】+=+=1++
=++3≥2+3=3+2,当且仅当a=2-,b=-1时取等号.
所以+的最小值是3+2.
答案:3+2
题15.若正实数x,y满足x++y+=10,则-的最大值是__________.
【解析】由题意可得x++y+-10=0,
所以-=x++y+-10≥2+2-10=-4,
所以-≤4,
当且仅当时,等号成立,
因此-的最大值是4.
答案:4
题16.若A=(-2,5),则以A为解集的一个一元二次不等式可以是__________.
【解析】设关于x的一元二次不等式ax2+bx+c<0的解集为(-2,5).
则-2和5是关于x的一元二次不等式ax2+bx+c=0的两根,且a>0.
即,不妨设a=1,解得b=-3,c=-10.
所以以A为解集的一个一元二次不等式可以是x2-3x-10<0.
答案:x2-3x-10<0(答案不唯一)
题17.某种商品计划提价,现有四种方案:
方案(1)先提价m%,再提价n%;
方案(2)先提价n%,再提价m%;
方案(3)分两次提价,每次提价%;
方案(4)一次性提价(m+n)%.
已知m>n>0,那么四种提价方案中,提价最多的是哪种方案?
【解析】依题意,设单价为1,方案(1)提价后的价格是(1+)(1+)=1++;
方案(2)提价后的价格是=1++;
方案(3)提价后的价格是=1++;
方案(4)提价后的价格是1+,
所以,提价最少的是方案(4),方案(1)和方案(2)提价后的价格是一样的,
只需比较与的大小即可,因为m>n>0,则(m-n)2>0,
所以-==>0,所以(1+)2>(1+)(1+),因此方案(3)提价最多.
题18.若a,b,c都是正数,求证:a2+b2+c2≥++.
【证明】欲证原不等式即证:
++≥++.即可分别证明如下三个不等式:≥,≥,≥.
而要证≥,可寻找适当的媒介不等式.
因为a,b都是正数,所以≥,≥,
于是++≥++.
因为≥,
所以a2+b2+c2≥++成立.
这样原不等式一定成立.
题19.设二次函数y=ax2+bx+c(a≠0).
(1)若b=2,c=-1且二次函数的最大值为正数,求a的取值范围.
(2)若ax2-x-2<0的解集是,求y>c2的解集.
(3)设二次函数y=ax2+bx+c(a>0)的两个零点分别为x1,x2,满足0<x1<x2<,证明:当x∈(0,x1)时,0<y<x1-x.
【解析】(1)当b=2,c=-1时,y=ax2+2x-1,
由最大值为正数可得a<0,4+4a>0,
则-1<a<0,即a的取值范围是(-1,0).
(2)由题意知b,2为方程ax2-x-2=0两解,
则b+2=,2b=,解得a=1,b=-1,又y>c2,
即x2-x+c>c2,又x2-x-(c2-c)>0,则[x+(c-1)](x-c)>0,
当-(c-1)<c,即c>时,解集为(-∞,-c+1)∪(c,+∞);
当-(c-1)=c,即c=时,解集为(-∞,)∪(,+∞);
当-(c-1)>c,即c<时,解集为(-∞,c)∪(-c+1,+∞).
(3)由二次函数y=ax2+bx+c(a>0)的两个零点分别为x1,x2,
可得y=a(x-x1)(x-x2),x∈(0,x1)时,x-x1<0,x-x2<0,a>0,则y>0;
y+x-x1=a(x-x1)(x-x2)+x-x1=(x-x1)[a(x-x2)+1],
由0<x1<x2<,x∈(0,x1)时-<x-x2<0,则a(x-x2)+1>0,
由x-x1<0,则y+x-x1<0,y<x1-x.
综上,0<y<x1-x.
题20.中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为3 m,底面积为12 m2,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体的报价为每平方米150元,屋顶和地面以及其他报价共计7 200元,设屋子的左右两面墙的长度均为x m(2≤x≤6).
(1)当左右两面墙的长度为多少米时,甲工程队的报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(a>0);若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,求a的取值范围.
【解析】(1)设甲工程队的总造价为y元,依题意左右两面墙的长度均为x m(2≤x≤6),则屋子前面新建墙体长为 m,
则y=3(150×2x+400×)+7 200=900(x+)+7 200(2≤x≤6).
因为900+7 200≥900×2×+7 200=14 400.
当且仅当x=,即x=4时等号成立.
所以当x=4时,ymin=14 400,
即当左右两面墙的长度为4 m时,甲工程队的报价最低为14 400元.
(2)由题意可得,900(x+)+7 200>对任意的x∈[2,6]恒成立.
即>,从而>a,即x+1++6>a恒成立,
又x+1++6≥2+6=12.
当且仅当x+1=,即x=2时等号成立.
所以0<a<12,即a的取值范围是{a|0<a<12}.
- 0 -
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、理解并掌握不等式基本性质.
2、理解并掌握基本不等式及其应用.
3、会求解与一元二次不等式有关的综合问题.
本节重点难点
重点:基本不等式及其应用;
难点:求解与一元二次不等式有关的综合问题.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
构建网络结构简图
1. 实数比较大小的基本事实
文字语言 符号表示
如果a>b,那么a-b是______; 如果a<b,那么a-b是______; 如果a=b,那么a-b等于______ a>b a-b____0 a<b a-b____0 a=b a-b____0
2.不等式的基本性质
别名 性质内容 注意
性质1 对称性 a>b b____a 可逆
性质2 传递性 a>b,b>c ____ 同向
性质3 可加性 a>b ________ 可逆
性质3 的推论 移项 法则 a+b>c a____c-b 可逆
性质4 可乘性 a>b,c>0 ac____bc a>b,c<0 _____ c的 符号
性质5 同向可加性 a>b,c>d ______ 同向
性质6 同向同 正可乘性 a>b>0,c>d>0 ______ 同向 同正
3. 算术平均数与几何平均数
对于正数a,b,我们把__________称为a,b的算术平均数,________称为a,b的几何平均数.
4.基本不等式
(1)公式:
①条件:a,b是正数;
②结论:___________________;
③等号成立:当且仅当a=b时.
(2)本质:基本不等式表明,两个正数的算术平均数不小于它们的几何平均数.
(3)变形式:当a,b∈R时,a2+b2____2ab,a2+b2+2ab______4ab,ab _____,
Ab____(当且仅当a=b时,等号成立).
5.用基本不等式求最值的结论
对于正数a,b,
(1)和a+b为定值时,积ab有最____值;积ab为定值时,和a+b有最____值.
(2)取等号的条件:当且仅当________时,=.
(3)应用:求和式的最小值,乘积式的最大值.
6. 二次函数的零点
一般地,一元二次方程的根就是二次函数当函数值取零时____________,即二次函数的图象与_______________,也称为二次函数的零点.
7.一元二次方程的根、二次函数的图象、二次函数的零点之间的关系
(1)关系(当a>0时).
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根
二次函数的零点
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
8. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的____________叫作一元二次不等式.
9.一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集 _______________ _______________
二次函数的解集 ______________ ______________ _____________
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【综合复习题练】
题1.已知-3<a<-2,3<b<4,则的取值范围为( )
A.(1,3) B.
C. D.
题2.已知a,b∈R,则“>”是“<”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
题3.若a>b>0,m>0,n>0,则,,,按由小到大的顺序排列为( )
A.<<<
B.<<<
C.<<<
D.<<<
题4.若两个正实数x,y满足4x+y=xy且存在这样的x,y使不等式x+<m2+3m有解,则实数m的取值范围是( )
A.(-1,4)
B.(-4,1)
C.(-∞,-4)∪(1,+∞)
D.(-∞,-3)∪(0,+∞)
题5.设x>0,y>0,且=,则当x+取最小值时,x2+=( )
A.12 B.8 C.16 D.
题6.已知a,b∈R且ab≠0,若对任意的x≤0均有(x-a)(x-b)(x-2a-b)≤0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
题7.已知0<a<1,0<b<1,且4(a+b)=4ab+3,则a+2b的最大值为( )
A.2 B.2
C.3- D.3-2
题8.若实数x,y,z满足,记P=xy+yz+xz+y2,Q=x+2y+z,则P与Q的大小关系是( )
A.P<Q B.P>Q
C.P=Q D.不确定
题9(多选题).下列结论不正确的是( )
A.<<0 |a|>|b|
B.> a>b
C. <
D. <
题10(多选题).周长为3+2的直角三角形的面积可能为( )
A.3 B.3
C. D.
题11(多选题).已知不等式x2+ax+b>0(a>0)的解集是{x|x≠d},则下列四个结论中正确的是( )
A.a2=4b
B.a2+≥4
C.若不等式x2+ax-b<0的解集为(x1,x2),则x1x2>0
D.若不等式x2+ax+b<c的解集为(x1,x2),且|x1-x2|=4,则c=4
题12(多选题).下列关于一元二次不等式叙述正确的是( )
A.若一元二次不等式ax2+bx+c>0的解集为 ,则a<0,且Δ≤0
B.若==,则一元二次不等式a1x2+b1x+c1>0的解集与一元二次不等式a2x2+b2x+c2>0的解集相等
C.已知a∈Z,关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则所有符合条件的a的值之和是22
D.若一元二次不等式ax2+bx+c≥0的解集为R,且b>a,则的最小值为3
题13.若-10<a<b<8,则a+b的取值范围是__________;+b的取值范围是__________.
题14.已知正实数a,b满足a+b=1,则+的最小值是__________.
题15.若正实数x,y满足x++y+=10,则-的最大值是__________.
题16.若A=(-2,5),则以A为解集的一个一元二次不等式可以是__________.
题17.某种商品计划提价,现有四种方案:
方案(1)先提价m%,再提价n%;
方案(2)先提价n%,再提价m%;
方案(3)分两次提价,每次提价%;
方案(4)一次性提价(m+n)%.
已知m>n>0,那么四种提价方案中,提价最多的是哪种方案?
题18.若a,b,c都是正数,求证:a2+b2+c2≥++.
题19.设二次函数y=ax2+bx+c(a≠0).
(1)若b=2,c=-1且二次函数的最大值为正数,求a的取值范围.
(2)若ax2-x-2<0的解集是,求y>c2的解集.
(3)设二次函数y=ax2+bx+c(a>0)的两个零点分别为x1,x2,满足0<x1<x2<,证明:当x∈(0,x1)时,0<y<x1-x.
题20.中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为3 m,底面积为12 m2,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体的报价为每平方米150元,屋顶和地面以及其他报价共计7 200元,设屋子的左右两面墙的长度均为x m(2≤x≤6).
(1)当左右两面墙的长度为多少米时,甲工程队的报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(a>0);若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,求a的取值范围.
编号:017 课题: §3 不等式复习课
教学课时安排
1、上课时间:_________________.
2、课时安排:_________________.
3、上课班级___________________.
学科目标要求
1、理解并掌握不等式基本性质.
2、理解并掌握基本不等式及其应用.
3、会求解与一元二次不等式有关的综合问题.
本节重点难点
重点:基本不等式及其应用;
难点:求解与一元二次不等式有关的综合问题.
学科素养目标
在本章教材注重突出不等式的实际背景和实际运用,通过对背景的分析、概括和抽象,建立不等式模型,进而对不等式模型进行数学研究,最后再回到实际问题中.这里的展开过程与教材的其它章节是一致的,即按照数学研究的一般程序进行展开.(如图)
教材在研究一元二次不等式的图象解法时,首先提出这样的问题“一元二次不等式与相应的二次函数是否有内在的联系?” 这为学生的活动与发现提供了基础,也为研究不等式的解法指明了方向,即数形结合.教材在研究线性规划的求解方法时,也运用了数形结合的思想方法.
基础知识积累
构建网络结构简图
1. 实数比较大小的基本事实
文字语言 符号表示
如果a>b,那么a-b是_正数_; 如果a<b,那么a-b是_负数_; 如果a=b,那么a-b等于_0_ a>b a-b_>_0 a<b a-b_<_0 a=b a-b_=_0
2.不等式的基本性质
别名 性质内容 注意
性质1 对称性 a>b b < a 可逆
性质2 传递性 a>b,b>c a>c 同向
性质3 可加性 a>b a+c>b+c 可逆
性质3 的推论 移项 法则 a+b>c a > c-b 可逆
性质4 可乘性 a>b,c>0 ac > bc a>b,c<0 ac
性质6 同向同 正可乘性 a>b>0,c>d>0 ac>bd 同向 同正
3. 算术平均数与几何平均数
对于正数a,b,我们把 称为a,b的算术平均数, 称为a,b的几何平均数.
4.基本不等式
(1)公式:
①条件:a,b是正数;
②结论: ;
③等号成立:当且仅当a=b时.
(2)本质:基本不等式表明,两个正数的算术平均数不小于它们的几何平均数.
(3)变形式:当a,b∈R时,a2+b2 ≥ 2ab,a2+b2+2ab ≥ 4ab,ab ≤ ,
ab ≤ (当且仅当a=b时,等号成立).
5.用基本不等式求最值的结论
对于正数a,b,
(1)和a+b为定值时,积ab有最 大 值;积ab为定值时,和a+b有最 小 值.
(2)取等号的条件:当且仅当 a=b 时, .
(3)应用:求和式的最小值,乘积式的最大值.
6. 二次函数的零点
一般地,一元二次方程的根就是二次函数当函数值取零时_自变量的值_,即二次函数的图象与__轴交点的横坐标____,也称为二次函数的零点.
7.一元二次方程的根、二次函数的图象、二次函数的零点之间的关系
(1)关系(当a>0时).
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的零点 有两个零点 有一个零点 无零点
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
8. 一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是2的_整式不等式_叫作一元二次不等式.
9.一元二次不等式和相应的二次函数的对应关系
(1)关系:(a>0)
二次函数 ()的图象
一元二次方程 有两相异实根 有两相等实根 没有实数根
二次函数的解集
二次函数的解集
(2)本质:判别式Δ>0,Δ=0,Δ<0的情况决定着一元二次方程根、二次函数图象与x轴交点和二次函数零点的情况.
(3)应用:①求二次函数的零点;②证明二次函数零点的个数;③判断二次函数零点所在的区间.
【综合复习题练】
题1.已知-3<a<-2,3<b<4,则的取值范围为( )
A.(1,3) B.
C. D.
【解析】选A.因为-3<a<-2,所以a2∈(4,9),而3<b<4,所以<<,故的取值范围为(1,3).
题2.已知a,b∈R,则“>”是“<”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【解析】选C.由>得a2+b2-2ab>b2,所以a(a-2b)>0,
所以>0,所以1->0,所以<.反之,也成立.
所以“>”是“<”的充要条件.
题3.若a>b>0,m>0,n>0,则,,,按由小到大的顺序排列为( )
A.<<<
B.<<<
C.<<<
D.<<<
【解析】选A.-==,
因为a>b>0,m>0,所以<0,所以<,-
=
=,
因为a>b>0,m>0,n>0,
所以<0,
所以<,-==,
因为a>b>0,n>0,所以<0,所以<,所以<<<.
题4.若两个正实数x,y满足4x+y=xy且存在这样的x,y使不等式x+<m2+3m有解,则实数m的取值范围是( )
A.(-1,4)
B.(-4,1)
C.(-∞,-4)∪(1,+∞)
D.(-∞,-3)∪(0,+∞)
【解析】选C.由4x+y=xy +=1知,
=1+++1≥2+2=4,当且仅当x=2,y=8时,等号成立,则使不等式x+<m2+3m有解,只需满足m2+3m>4即可,解得m的取值范围是(-∞,-4)∪(1,+∞).
题5.设x>0,y>0,且=,则当x+取最小值时,x2+=( )
A.12 B.8 C.16 D.
【解析】选A.因为x>0,y>0,所以当x+取最小值时,取最小值,
因为=x2++,=,所以x2+=+,
所以=+≥2=16,
所以x+≥4,当且仅当=,即x=2y时取等号,
所以x2++=16,所以x2++=16,
所以x2+=16-=12.
题6.已知a,b∈R且ab≠0,若对任意的x≤0均有(x-a)(x-b)(x-2a-b)≤0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
【解析】选D.因为ab≠0,所以b≠ab+b,若对任意的x≤0均有(x-a)(x-b)(x-2a-b)≤0,则ab(2a+b)≥0,
所以a,b不可能同时为负,至少有一个为正,
①若a>0,b>0,显然成立;
②若a>0,b<0,则2a+b≤0,此时要使(x-a)(x-b)(x-2a-b)≤0在(-∞,0]上恒成立,则必有b=2a+b,则a=0,矛盾;
③若a<0,b>0,则2a+b≤0,此时要使(x-a)(x-b)(x-2a-b)≤0在(-∞,0]上恒成立,则必有a=2a+b,则a+b=0,符合题意;
综上,b>0.
题7.已知0<a<1,0<b<1,且4(a+b)=4ab+3,则a+2b的最大值为( )
A.2 B.2
C.3- D.3-2
【解析】选C.因为4(a+b)=4ab+3,所以4ab-4a-4b+3=0,
所以4ab-4a-4b+4=1,即ab-a-b+1=,
即(1-a)(1-b)=.令x=1-a>0,y=1-b>0,则a=1-x,b=1-y,y=,
所以a+2b=1-x+2(1-y)=-x-2y+3=-x-+3
=-(x+)+3≤-2+3
=3-(当且仅当x=,即x=时,等号成立).
故a+2b的最大值为3-.
题8.若实数x,y,z满足,记P=xy+yz+xz+y2,Q=x+2y+z,则P与Q的大小关系是( )
A.P<Q B.P>Q
C.P=Q D.不确定
【解析】选A.P-Q=xy+yz+xz+y2-(x+2y+z)=xz+(y-1)(x+z)+(y-1)2-1=(x+y-1)(z+y-1)-1,
因为,所以x+y-1∈(0,1),z+y-1∈(0,1),
所以(x+y-1)(z+y-1)∈(0,1),
所以P-Q<1-1=0,即P<Q.
题9(多选题).下列结论不正确的是( )
A.<<0 |a|>|b|
B.> a>b
C. <
D. <
【解析】选ABD.A:因为<<0,所以ab>0且->->0,
因此-·ab>-·ab>0·ab,
即-b>-a>0 >>0 >,故A不正确,符合题意;
B:因为>,显然4>8不成立,所以B不正确,符合题意;
C:由a3>b3 a3-b3=(a-b)(a2+ab+b2)>0,而ab>0,
所以有a>b,而-=<0 <,故C正确,不符合题意;
D:若a=-2,b=-1,显然成立,但是<不成立,故D不正确,符合题意.
题10(多选题).周长为3+2的直角三角形的面积可能为( )
A.3 B.3
C. D.
【解析】选CD.设直角三角形的三边分别为a,b,c且c为斜边,
所以a+b+c=3+2 a+b+=3+2 3+2≥2+ ab≤,而直角三角形的面积S=≤,当且仅当a=b时等号成立,而a=b时,可得,
所以0<S≤.所以C,D满足题意.
题11(多选题).已知不等式x2+ax+b>0(a>0)的解集是{x|x≠d},则下列四个结论中正确的是( )
A.a2=4b
B.a2+≥4
C.若不等式x2+ax-b<0的解集为(x1,x2),则x1x2>0
D.若不等式x2+ax+b<c的解集为(x1,x2),且|x1-x2|=4,则c=4
【解析】选ABD.由题意得Δ=a2-4b=0,所以a2=4b,所以A正确;
对于B:a2+=a2+≥2=4,当且仅当a2=,即a=时等号成立,所以B正确;
对于C:由根与系数的关系,知x1x2=-b=-<0,所以C错误;
对于D:由根与系数的关系,知x1+x2=-a,x1x2=b-c=-c,
则|x1-x2|===2=4,解得c=4,所以D正确.
题12(多选题).下列关于一元二次不等式叙述正确的是( )
A.若一元二次不等式ax2+bx+c>0的解集为 ,则a<0,且Δ≤0
B.若==,则一元二次不等式a1x2+b1x+c1>0的解集与一元二次不等式a2x2+b2x+c2>0的解集相等
C.已知a∈Z,关于x的一元二次不等式x2-6x+a≤0的解集中有且仅有3个整数,则所有符合条件的a的值之和是22
D.若一元二次不等式ax2+bx+c≥0的解集为R,且b>a,则的最小值为3
【解析】选AD.对A,若一元二次不等式ax2+bx+c>0的解集为 ,
则ax2+bx+c≤0恒成立,所以a<0,且Δ≤0,故A正确;
对B,若a1和a2的符号相反,则两个一元二次不等式解集不同,故B错误;
对C,设f(x)=x2-6x+a=(x-3)2+a-9,
有,解得5<a≤8,由a∈Z,知a=6,7,8,和为21,故C错误;
对D,则有a>0,Δ=b2-4ac=0,所以b>a>0,
令t=,则t>1,t-1>0,
=====++≥2+=3,
当且仅当=,即t=4时取等号,故D正确.
题13.若-10<a<b<8,则a+b的取值范围是__________;+b的取值范围是__________.
【解析】当a≥0时,0≤a<8,0<b<8,故0<a+b<16,
而+b=a+b,所以0<+b<16;
当a<0时,-10<a<0,故0<=-a<10,
又-10<b<8,所以-20<a+b<8,-10<+b<18,
又a<b,所以+b>0,所以0<+b<18.
综上,a+b的取值范围是(-20,16),+b的取值范围是(0,18).
答案:(-20,16) (0,18)
题14.已知正实数a,b满足a+b=1,则+的最小值是__________.
【解析】+=+=1++
=++3≥2+3=3+2,当且仅当a=2-,b=-1时取等号.
所以+的最小值是3+2.
答案:3+2
题15.若正实数x,y满足x++y+=10,则-的最大值是__________.
【解析】由题意可得x++y+-10=0,
所以-=x++y+-10≥2+2-10=-4,
所以-≤4,
当且仅当时,等号成立,
因此-的最大值是4.
答案:4
题16.若A=(-2,5),则以A为解集的一个一元二次不等式可以是__________.
【解析】设关于x的一元二次不等式ax2+bx+c<0的解集为(-2,5).
则-2和5是关于x的一元二次不等式ax2+bx+c=0的两根,且a>0.
即,不妨设a=1,解得b=-3,c=-10.
所以以A为解集的一个一元二次不等式可以是x2-3x-10<0.
答案:x2-3x-10<0(答案不唯一)
题17.某种商品计划提价,现有四种方案:
方案(1)先提价m%,再提价n%;
方案(2)先提价n%,再提价m%;
方案(3)分两次提价,每次提价%;
方案(4)一次性提价(m+n)%.
已知m>n>0,那么四种提价方案中,提价最多的是哪种方案?
【解析】依题意,设单价为1,方案(1)提价后的价格是(1+)(1+)=1++;
方案(2)提价后的价格是=1++;
方案(3)提价后的价格是=1++;
方案(4)提价后的价格是1+,
所以,提价最少的是方案(4),方案(1)和方案(2)提价后的价格是一样的,
只需比较与的大小即可,因为m>n>0,则(m-n)2>0,
所以-==>0,所以(1+)2>(1+)(1+),因此方案(3)提价最多.
题18.若a,b,c都是正数,求证:a2+b2+c2≥++.
【证明】欲证原不等式即证:
++≥++.即可分别证明如下三个不等式:≥,≥,≥.
而要证≥,可寻找适当的媒介不等式.
因为a,b都是正数,所以≥,≥,
于是++≥++.
因为≥,
所以a2+b2+c2≥++成立.
这样原不等式一定成立.
题19.设二次函数y=ax2+bx+c(a≠0).
(1)若b=2,c=-1且二次函数的最大值为正数,求a的取值范围.
(2)若ax2-x-2<0的解集是,求y>c2的解集.
(3)设二次函数y=ax2+bx+c(a>0)的两个零点分别为x1,x2,满足0<x1<x2<,证明:当x∈(0,x1)时,0<y<x1-x.
【解析】(1)当b=2,c=-1时,y=ax2+2x-1,
由最大值为正数可得a<0,4+4a>0,
则-1<a<0,即a的取值范围是(-1,0).
(2)由题意知b,2为方程ax2-x-2=0两解,
则b+2=,2b=,解得a=1,b=-1,又y>c2,
即x2-x+c>c2,又x2-x-(c2-c)>0,则[x+(c-1)](x-c)>0,
当-(c-1)<c,即c>时,解集为(-∞,-c+1)∪(c,+∞);
当-(c-1)=c,即c=时,解集为(-∞,)∪(,+∞);
当-(c-1)>c,即c<时,解集为(-∞,c)∪(-c+1,+∞).
(3)由二次函数y=ax2+bx+c(a>0)的两个零点分别为x1,x2,
可得y=a(x-x1)(x-x2),x∈(0,x1)时,x-x1<0,x-x2<0,a>0,则y>0;
y+x-x1=a(x-x1)(x-x2)+x-x1=(x-x1)[a(x-x2)+1],
由0<x1<x2<,x∈(0,x1)时-<x-x2<0,则a(x-x2)+1>0,
由x-x1<0,则y+x-x1<0,y<x1-x.
综上,0<y<x1-x.
题20.中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为3 m,底面积为12 m2,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体的报价为每平方米150元,屋顶和地面以及其他报价共计7 200元,设屋子的左右两面墙的长度均为x m(2≤x≤6).
(1)当左右两面墙的长度为多少米时,甲工程队的报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(a>0);若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,求a的取值范围.
【解析】(1)设甲工程队的总造价为y元,依题意左右两面墙的长度均为x m(2≤x≤6),则屋子前面新建墙体长为 m,
则y=3(150×2x+400×)+7 200=900(x+)+7 200(2≤x≤6).
因为900+7 200≥900×2×+7 200=14 400.
当且仅当x=,即x=4时等号成立.
所以当x=4时,ymin=14 400,
即当左右两面墙的长度为4 m时,甲工程队的报价最低为14 400元.
(2)由题意可得,900(x+)+7 200>对任意的x∈[2,6]恒成立.
即>,从而>a,即x+1++6>a恒成立,
又x+1++6≥2+6=12.
当且仅当x+1=,即x=2时等号成立.
所以0<a<12,即a的取值范围是{a|0<a<12}.
- 0 -
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
