数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系 课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 744.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 19:11:37 | ||
图片预览





文档简介
(共19张PPT)
2.5.1
直线与圆的位置关系
学习目标
1.会用代数法和几何法探讨直线与圆的位置关系。
2.理解几何法和代数法在解决不同问题的优劣。
3.会利用直线与圆的位置关系解决相关问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
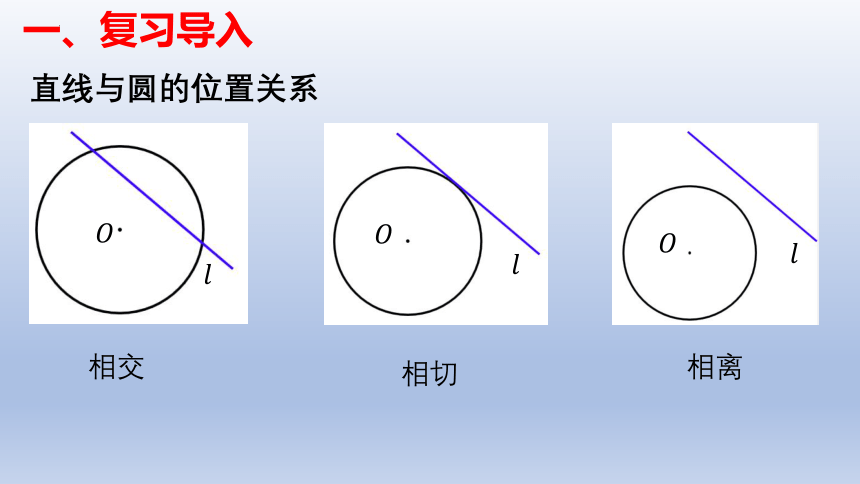
直线与圆的位置关系
相交
相切
相离
问题1:如何判断直线与圆的位置关系?
通过直线与圆的公共点个数判断
相交
有2个公共点
有1个公共点
相切
相离
有0个公共点
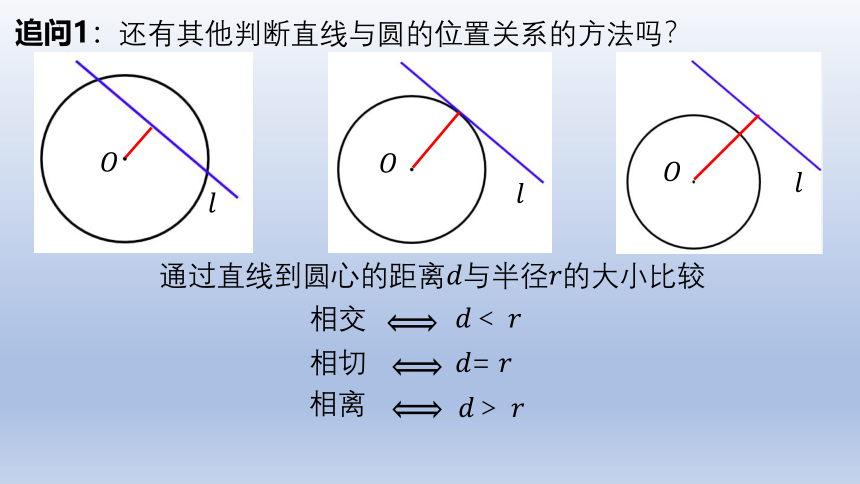
追问1:还有其他判断直线与圆的位置关系的方法吗?
通过直线到圆心的距离与半径的大小比较
相交
<
相切
=
相离
>
问题1:类比两直线的位置关系的研究过程,如何通过代数方法,研究直线与圆的位置关系?
二、新课讲授
1、直线与圆的位置关系
:3, :
法一:画图观察判断
法二(代数法):解方程组,由解的情况来判断
解得
画图:不能得到交点具体的位置,即无法得到交点的坐标.
问题1:类比两直线的位置关系的研究过程,如何通过代数方法,研究直线与圆的位置关系?
两直线的位置关系
联立两直线方程
方程组解的情况
直线与圆的位置关系
联立直线与圆方程
方程组解的情况
例1 已知直线:3和圆心为的圆 .
(1)判断直线与圆的位置关系;
(2)如果相交,求直线圆锁截得的弦长.
解法一:(1)联立直线与圆方程,得
消去,得: ,
由,可知方程有两组实数解.
所以直线与圆相交,有两个公共点.
(2)由(1)可知 ,解得
1
将 1分别代入方程①,可得
3
所以直线与圆的两个交点是
因此直线圆锁截得的弦长为
解题思路1:
几何—代数→联立、解方程组→代数—几何
位置关系 公共点个数
解题思路2:
几何—代数→求圆心的距离与半径→代数—几何
位置关系 与的比较
解法二:(1)圆的方程可化为=5,
因此圆心的坐标为(0,1),半径为,圆心到直线的距离为
= = <
所以直线与圆相交,有两个公共点.
B
C
A
解法二:(2)如图,由垂径定理,得
小结:
相交:直线与圆有两个公共点
相切:直线与圆有一个公共点
相离:直线与圆没有公共点
法一
法二
两组解
一组解
无解
<
=
>
联立方程
计算点线距离
三、巩固新知
例2 求过点作圆: =1的切线,求切线的方程.
追问1:点与圆的位置关系是什么?
点在圆外
追问2:过圆外一点做圆的切线,能做几条切线?
两条
追问3:如何刻画直线与圆相切?
公共点的个数;圆心到直线的距离
追问4:直线方程选择什么形式?
点斜式;两点式
点斜式
,圆心(0,0),半径1
= →
注意:运用点斜式必须先判断斜率是否存在
P
解法一:如图,首先考虑斜率不存在的情况,此时与圆相离,因此切线的斜率存在.
设切线的斜率为,则切线方程为
因为直线与圆相切,所以方程组
只有一组解.
消元,得
因为该方程只有一个解,所以
,
解得
所以,所求切线的方程为1,或0.
解法二:设切线的斜率为,则切线的方程为
即0
由圆心(0,0)到切线的距离等于圆的半径1,得
= = ,
解得
因此,所求切线的方程为1,或0.
两点式
联立方程,
求出切点A坐标,设切点A坐标为( ).
小结:两种方法的差异
直线与圆相切
直线方程
四、课堂小结
1、直线与圆的位置关系
五、作业布置
课本P93:练习 第2、3题
①联立直线与圆的方程,由判断实数解的个数,得到位置关系
②利用圆心到直线的距离与半径的大小关系判断,得到位置关系
2、由几何问题转化为代数问题:数形结合的思想
2.5.1
直线与圆的位置关系
学习目标
1.会用代数法和几何法探讨直线与圆的位置关系。
2.理解几何法和代数法在解决不同问题的优劣。
3.会利用直线与圆的位置关系解决相关问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
直线与圆的位置关系
相交
相切
相离
问题1:如何判断直线与圆的位置关系?
通过直线与圆的公共点个数判断
相交
有2个公共点
有1个公共点
相切
相离
有0个公共点
追问1:还有其他判断直线与圆的位置关系的方法吗?
通过直线到圆心的距离与半径的大小比较
相交
<
相切
=
相离
>
问题1:类比两直线的位置关系的研究过程,如何通过代数方法,研究直线与圆的位置关系?
二、新课讲授
1、直线与圆的位置关系
:3, :
法一:画图观察判断
法二(代数法):解方程组,由解的情况来判断
解得
画图:不能得到交点具体的位置,即无法得到交点的坐标.
问题1:类比两直线的位置关系的研究过程,如何通过代数方法,研究直线与圆的位置关系?
两直线的位置关系
联立两直线方程
方程组解的情况
直线与圆的位置关系
联立直线与圆方程
方程组解的情况
例1 已知直线:3和圆心为的圆 .
(1)判断直线与圆的位置关系;
(2)如果相交,求直线圆锁截得的弦长.
解法一:(1)联立直线与圆方程,得
消去,得: ,
由,可知方程有两组实数解.
所以直线与圆相交,有两个公共点.
(2)由(1)可知 ,解得
1
将 1分别代入方程①,可得
3
所以直线与圆的两个交点是
因此直线圆锁截得的弦长为
解题思路1:
几何—代数→联立、解方程组→代数—几何
位置关系 公共点个数
解题思路2:
几何—代数→求圆心的距离与半径→代数—几何
位置关系 与的比较
解法二:(1)圆的方程可化为=5,
因此圆心的坐标为(0,1),半径为,圆心到直线的距离为
= = <
所以直线与圆相交,有两个公共点.
B
C
A
解法二:(2)如图,由垂径定理,得
小结:
相交:直线与圆有两个公共点
相切:直线与圆有一个公共点
相离:直线与圆没有公共点
法一
法二
两组解
一组解
无解
<
=
>
联立方程
计算点线距离
三、巩固新知
例2 求过点作圆: =1的切线,求切线的方程.
追问1:点与圆的位置关系是什么?
点在圆外
追问2:过圆外一点做圆的切线,能做几条切线?
两条
追问3:如何刻画直线与圆相切?
公共点的个数;圆心到直线的距离
追问4:直线方程选择什么形式?
点斜式;两点式
点斜式
,圆心(0,0),半径1
= →
注意:运用点斜式必须先判断斜率是否存在
P
解法一:如图,首先考虑斜率不存在的情况,此时与圆相离,因此切线的斜率存在.
设切线的斜率为,则切线方程为
因为直线与圆相切,所以方程组
只有一组解.
消元,得
因为该方程只有一个解,所以
,
解得
所以,所求切线的方程为1,或0.
解法二:设切线的斜率为,则切线的方程为
即0
由圆心(0,0)到切线的距离等于圆的半径1,得
= = ,
解得
因此,所求切线的方程为1,或0.
两点式
联立方程,
求出切点A坐标,设切点A坐标为( ).
小结:两种方法的差异
直线与圆相切
直线方程
四、课堂小结
1、直线与圆的位置关系
五、作业布置
课本P93:练习 第2、3题
①联立直线与圆的方程,由判断实数解的个数,得到位置关系
②利用圆心到直线的距离与半径的大小关系判断,得到位置关系
2、由几何问题转化为代数问题:数形结合的思想
