人教A版必修第一册高一数学4.5.1函数的零点与方程的解 同步培优题典(含详细解析)
文档属性
| 名称 | 人教A版必修第一册高一数学4.5.1函数的零点与方程的解 同步培优题典(含详细解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 576.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 00:00:00 | ||
图片预览




文档简介
人教A版必修第一册高一数学4.4函数的零点与方程的解同步培优题典(原卷版)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·沈阳二中北校高三其他(文))函数的零点所在的区间是( )
A. B. C. D.
2.(2020·全国高三(文))函数的零点个数为( )
A.1 B.2 C.3 D.4
3.(2020·全国高三(文))已知函数在区间内有零点,则正数的取值范围为( )
A. B. C. D.
4.(2020·全国高三(文))若函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确到0.1)为( )
A.1.2 B.1.3 C.1.4 D.1.5
5.(2020·全国高一专题练习)某同学用二分法求方程在x∈(1,2)内近似解的过程中,设
,且计算f(1)<0,f(2)>0,f(1.5)>0,则该同学在第二次应计算的函数值为
A.f(0.5) B.f(1.125)
C.f(1.25) D.f(1.75)
6.(2020·浙江高一课时练习)当时,,,的大小关系是( )
A. B.
C. D.
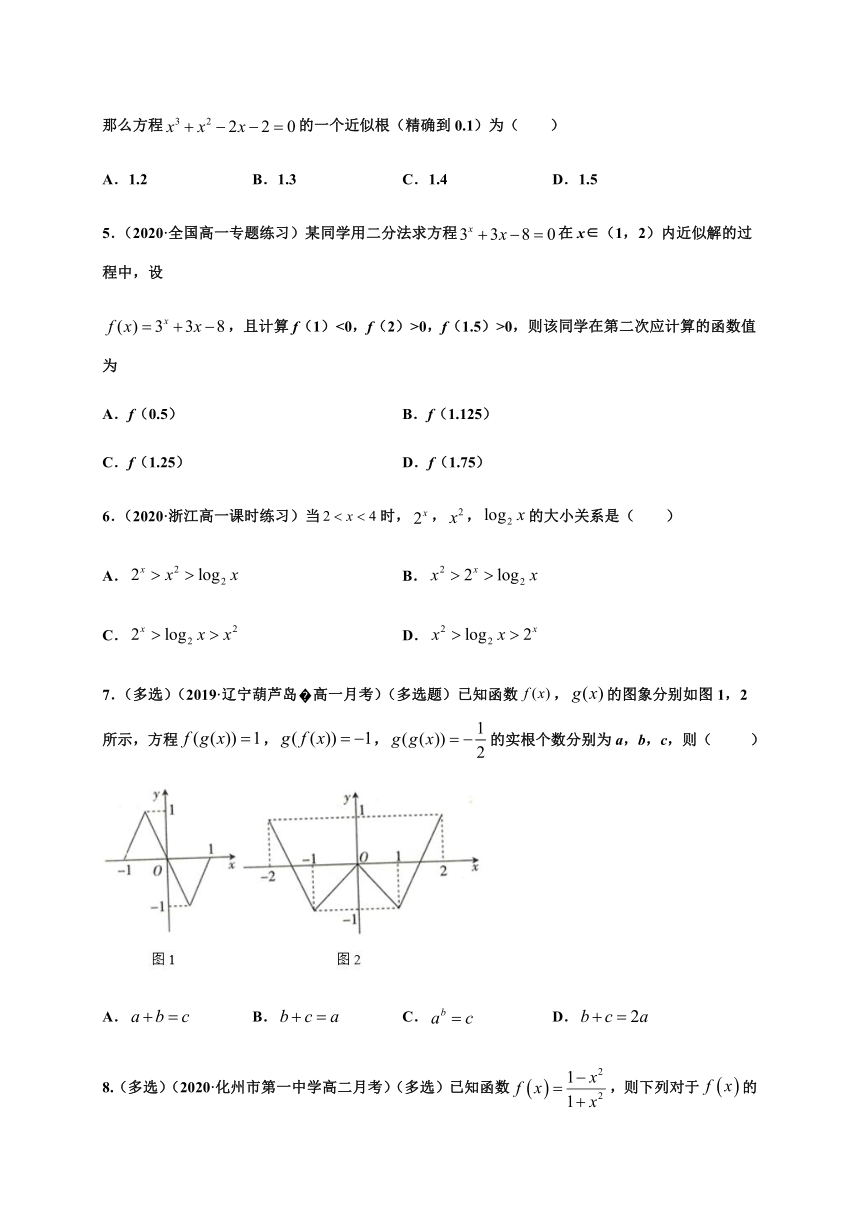
7.(多选)(2019·辽宁葫芦岛 高一月考)(多选题)已知函数,的图象分别如图1,2所示,方程,,的实根个数分别为a,b,c,则( )
A. B. C. D.
8.(多选)(2020·化州市第一中学高二月考)(多选)已知函数,则下列对于的性质表述正确的是( )
A.为偶函数
B.
C.在上的最大值为
D.在区间上至少有一个零点
二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
9.(2020·全国高一课时练习)若二次函数的两个零点分别是和,则的值为________.
10.(2020·全国高一课时练习)若函数有零点,则实数k的取值范围是________.
11.(2020·全国高三(文))若函数的一个零点在区间内,则实数的取值范围是________.
12.(一题双空)(2018·北京海淀 人大附中高三零模(理))已知函数,
①若a=1,f(x)的最小值是_____;
②若f(x)恰好有2个零点,则实数a的取值范围是_____.
三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
13.(2020·浙江高一课时练习)如图,建立平面直角坐标系,轴在地平面上,轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上,其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标不超过多少时,炮弹可以击中它?请说明理由.
14.(2020·浙江高一单元测试)研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数,单位是,其中x表示鲑鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是8100个单位时,它的游速是多少?
(2)计算一条鲑鱼静止时耗氧量的单位数.
(3)若鲑鱼A的游速大于鲑鱼B的游速,问这两条鲑鱼谁的耗氧量较大?并说明理由.
15.(2020·浙江高一课时练习)某企业生产一种机器的固定成本(即固定投入)为0.5万元,但每生产1百台时又需可变成本(即需另增加投入)0.25万元,市场对此商品的需求量为5百台,销售收入(单位:万元)的函数为,其中x是产品生产并售出的数量(单位:百台).
(1)把利润表示为年产量的函数.
(2)年产量为多少时,企业所得利润最大?
(3)年产量为多少时,企业才不亏本(不赔钱)?
16.(2020·浙江高一单元测试)甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图所示(1),该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1)(2)
(1)写出图(1)表示的销售价格与时间的函数关系式,写出图(2)表示的日销售量与时间的函数关系式及日销售金额M(元)与时间的函数关系式.
(2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系式为,试比较4月份每天两商店销售金额的大小关系。
人教A版必修第一册高一数学4.4函数的零点与方程的解同步培优题典(原卷版)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·沈阳二中北校高三其他(文))函数的零点所在的区间是( )
A. B. C. D.
【答案】B
【解析】∵,,则,
∴函数的零点所在区间是 ,
当,且时,
,
,
,
ACD中函数在区间端点的函数值均同号,根据零点存在性定理,B为正确答案.故选:B.
2.(2020·全国高三(文))函数的零点个数为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】函数f(x)=ex|lnx|﹣2的零点可以转化为:|lnx|的零点;
在坐标系中画出两个函数的图象,根据图象可得有两个交点;
故原函数有两个零点.故选:B.
3.(2020·全国高三(文))已知函数在区间内有零点,则正数的取值范围为( )
A. B. C. D.
【答案】A
【解析】由题得,且函数在定义域内单调递增(增+增=增),
所以,得.故选:A
4.(2020·全国高三(文))若函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确到0.1)为( )
A.1.2 B.1.3 C.1.4 D.1.5
【答案】C
【解析】由表中参考数据可得,,,
所以,由二分法定义得零点应该存在于区间内,又
精确度为,且,故方程的一个近似根为.
故选:C
5.(2020·全国高一专题练习)某同学用二分法求方程在x∈(1,2)内近似解的过程中,设
,且计算f(1)<0,f(2)>0,f(1.5)>0,则该同学在第二次应计算的函数值为
A.f(0.5) B.f(1.125)
C.f(1.25) D.f(1.75)
【答案】C
【解析】∵f(1)<0,f(2)>0,f(1.5)>0,∴在区间(1,1.5)内函数f(x)=3x+3x–8存在一个零点,该同学在第二次应计算的函数值1.25,故选C.
6.(2020·浙江高一课时练习)当时,,,的大小关系是( )
A. B.
C. D.
【答案】B
【解析】在平面直角坐标系中,作出,,在时的图象如下图所示:
由图象可知,当时,
故选:
7.(多选)(2019·辽宁葫芦岛 高一月考)(多选题)已知函数,的图象分别如图1,2所示,方程,,的实根个数分别为a,b,c,则( )
A. B. C. D.
【答案】AD
【解析】由图,方程,,此时对应4个解,故;
方程,得或者,此时有2个解,故;
方程,取到4个值,如图所示:
即或或或,则对应的的解,有6个,故.
根据选项,可得A,D成立.故选:AD.
8.(多选)(2020·化州市第一中学高二月考)(多选)已知函数,则下列对于的性质表述正确的是( )
A.为偶函数
B.
C.在上的最大值为
D.在区间上至少有一个零点
【答案】ABCD
【解析】因为,所以其的定义域为,
A选项,,所以函数为偶函数,故A正确;
B选项,,故B正确;
C选项,因为,当,单调递增,所以单调递减,因此,故C正确;
D选项,因为,所以,,
即,由零点存在性定理可得:在区间上存在零点,故D正确;故选ABCD
二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
9.(2020·全国高一课时练习)若二次函数的两个零点分别是和,则的值为________.
【答案】
【解析】由于二次函数的两个零点分别是和,由韦达定理得,解得,因此,.故答案为:.
10.(2020·全国高一课时练习)若函数有零点,则实数k的取值范围是________.
【答案】(0,1]
【解析】有零点,即k∈ 而-|x|≤0,0<≤20=1,∴的值域为(0,1].所以k的取值范围是(0,1]故答案为:(0,1]
11.(2020·全国高三(文))若函数的一个零点在区间内,则实数的取值范围是________.
【答案】.
【解析】由条件可知函数在上单调递增,所以,即,解之得.所以实数的取值范围是.
故答案为:
12.(一题双空)(2018·北京海淀 人大附中高三零模(理))已知函数,
①若a=1,f(x)的最小值是_____;
②若f(x)恰好有2个零点,则实数a的取值范围是_____.
【答案】﹣
【解析】(1)由题意,
时,单调递增,,
时,,,
所以时,;
(2)若,则,恰有两个零点0和1,满足题意,
若,则时,无零点,
但时,有两个零点和,满足题意,
当时,则时,是增函数,,有一个零点,
时,由得或,因为只有两个零点,所以,解得,综上,的取值范围是.
三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
13.(2020·浙江高一课时练习)如图,建立平面直角坐标系,轴在地平面上,轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上,其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标不超过多少时,炮弹可以击中它?请说明理由.
【答案】(1)炮的最大射程是10千米.
(2)当不超过6千米时,炮弹可以击中目标.
【解析】(1)令y=0,得kx-(1+k2)x2=0,
由实际意义和题设条件知x>0,k>0,
故x==≤=10,当且仅当k=1时取等号.所以炮的最大射程为10千米.
(2)因为a>0,所以炮弹可击中目标
存在k>0,使3.2=ka-(1+k2)a2成立
关于k的方程a2k2-20ak+a2+64=0有正根
判别式Δ=(-20a)2-4a2(a2+64)≥0
a≤6.
所以当a不超过6(千米)时,可击中目标.
14.(2020·浙江高一单元测试)研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数,单位是,其中x表示鲑鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是8100个单位时,它的游速是多少?
(2)计算一条鲑鱼静止时耗氧量的单位数.
(3)若鲑鱼A的游速大于鲑鱼B的游速,问这两条鲑鱼谁的耗氧量较大?并说明理由.
【答案】(1);(2)一条鲑鱼静止时的耗氧量为100个单位;(3)鲑鱼A的耗氧量较大.
【解析】(1)将代入函数关系式,得,
所以一条鲑鱼的耗氧量是8100个单位时,它的游速是.
(2)令,得,即,则,所以一条鲑鱼静止时的耗氧量为100个单位.
(3)鲑鱼A的耗氧量较大.
理由:由,得,即,则,
所以鲑鱼A的耗氧量较大.
15.(2020·浙江高一课时练习)某企业生产一种机器的固定成本(即固定投入)为0.5万元,但每生产1百台时又需可变成本(即需另增加投入)0.25万元,市场对此商品的需求量为5百台,销售收入(单位:万元)的函数为,其中x是产品生产并售出的数量(单位:百台).
(1)把利润表示为年产量的函数.
(2)年产量为多少时,企业所得利润最大?
(3)年产量为多少时,企业才不亏本(不赔钱)?
【答案】(1);(2)475台;(3)年产量在11台到4800台之间时,企业不亏本.
【解析】(1)设利润为y万元,
得
即
(2)显然当时,企业会获得最大利润,
此时,,
,即年产量为475台时,企业所得利润最大.
(3)要使企业不亏本,则.
即或
得或,即.
即年产量在11台到4800台之间时,企业不亏本.
16.(2020·浙江高一单元测试)甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图所示(1),该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1)(2)
(1)写出图(1)表示的销售价格与时间的函数关系式,写出图(2)表示的日销售量与时间的函数关系式及日销售金额M(元)与时间的函数关系式.
(2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系式为,试比较4月份每天两商店销售金额的大小关系。
【答案】(1);(2)4月份的前11天甲商店每天的销售金额比乙商店少,以后乙商店每天的销售金额均比甲商店少
【解析】(1)设销售价格与时间之间的函数关系式是,
将(0,15),(30,30)代入得解得
∴.
设日销售量与时间之间的函数关系式为,
将(0,160),(30,40)代入得解得,
∴
故
(2)∵,
∴.
当时,;当时,.
即4月份的前11天甲商店每天的销售金额比乙商店少,以后乙商店每天的销售金额均比甲商店少.
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·沈阳二中北校高三其他(文))函数的零点所在的区间是( )
A. B. C. D.
2.(2020·全国高三(文))函数的零点个数为( )
A.1 B.2 C.3 D.4
3.(2020·全国高三(文))已知函数在区间内有零点,则正数的取值范围为( )
A. B. C. D.
4.(2020·全国高三(文))若函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确到0.1)为( )
A.1.2 B.1.3 C.1.4 D.1.5
5.(2020·全国高一专题练习)某同学用二分法求方程在x∈(1,2)内近似解的过程中,设
,且计算f(1)<0,f(2)>0,f(1.5)>0,则该同学在第二次应计算的函数值为
A.f(0.5) B.f(1.125)
C.f(1.25) D.f(1.75)
6.(2020·浙江高一课时练习)当时,,,的大小关系是( )
A. B.
C. D.
7.(多选)(2019·辽宁葫芦岛 高一月考)(多选题)已知函数,的图象分别如图1,2所示,方程,,的实根个数分别为a,b,c,则( )
A. B. C. D.
8.(多选)(2020·化州市第一中学高二月考)(多选)已知函数,则下列对于的性质表述正确的是( )
A.为偶函数
B.
C.在上的最大值为
D.在区间上至少有一个零点
二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
9.(2020·全国高一课时练习)若二次函数的两个零点分别是和,则的值为________.
10.(2020·全国高一课时练习)若函数有零点,则实数k的取值范围是________.
11.(2020·全国高三(文))若函数的一个零点在区间内,则实数的取值范围是________.
12.(一题双空)(2018·北京海淀 人大附中高三零模(理))已知函数,
①若a=1,f(x)的最小值是_____;
②若f(x)恰好有2个零点,则实数a的取值范围是_____.
三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
13.(2020·浙江高一课时练习)如图,建立平面直角坐标系,轴在地平面上,轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上,其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标不超过多少时,炮弹可以击中它?请说明理由.
14.(2020·浙江高一单元测试)研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数,单位是,其中x表示鲑鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是8100个单位时,它的游速是多少?
(2)计算一条鲑鱼静止时耗氧量的单位数.
(3)若鲑鱼A的游速大于鲑鱼B的游速,问这两条鲑鱼谁的耗氧量较大?并说明理由.
15.(2020·浙江高一课时练习)某企业生产一种机器的固定成本(即固定投入)为0.5万元,但每生产1百台时又需可变成本(即需另增加投入)0.25万元,市场对此商品的需求量为5百台,销售收入(单位:万元)的函数为,其中x是产品生产并售出的数量(单位:百台).
(1)把利润表示为年产量的函数.
(2)年产量为多少时,企业所得利润最大?
(3)年产量为多少时,企业才不亏本(不赔钱)?
16.(2020·浙江高一单元测试)甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图所示(1),该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1)(2)
(1)写出图(1)表示的销售价格与时间的函数关系式,写出图(2)表示的日销售量与时间的函数关系式及日销售金额M(元)与时间的函数关系式.
(2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系式为,试比较4月份每天两商店销售金额的大小关系。
人教A版必修第一册高一数学4.4函数的零点与方程的解同步培优题典(原卷版)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·沈阳二中北校高三其他(文))函数的零点所在的区间是( )
A. B. C. D.
【答案】B
【解析】∵,,则,
∴函数的零点所在区间是 ,
当,且时,
,
,
,
ACD中函数在区间端点的函数值均同号,根据零点存在性定理,B为正确答案.故选:B.
2.(2020·全国高三(文))函数的零点个数为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】函数f(x)=ex|lnx|﹣2的零点可以转化为:|lnx|的零点;
在坐标系中画出两个函数的图象,根据图象可得有两个交点;
故原函数有两个零点.故选:B.
3.(2020·全国高三(文))已知函数在区间内有零点,则正数的取值范围为( )
A. B. C. D.
【答案】A
【解析】由题得,且函数在定义域内单调递增(增+增=增),
所以,得.故选:A
4.(2020·全国高三(文))若函数的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程的一个近似根(精确到0.1)为( )
A.1.2 B.1.3 C.1.4 D.1.5
【答案】C
【解析】由表中参考数据可得,,,
所以,由二分法定义得零点应该存在于区间内,又
精确度为,且,故方程的一个近似根为.
故选:C
5.(2020·全国高一专题练习)某同学用二分法求方程在x∈(1,2)内近似解的过程中,设
,且计算f(1)<0,f(2)>0,f(1.5)>0,则该同学在第二次应计算的函数值为
A.f(0.5) B.f(1.125)
C.f(1.25) D.f(1.75)
【答案】C
【解析】∵f(1)<0,f(2)>0,f(1.5)>0,∴在区间(1,1.5)内函数f(x)=3x+3x–8存在一个零点,该同学在第二次应计算的函数值1.25,故选C.
6.(2020·浙江高一课时练习)当时,,,的大小关系是( )
A. B.
C. D.
【答案】B
【解析】在平面直角坐标系中,作出,,在时的图象如下图所示:
由图象可知,当时,
故选:
7.(多选)(2019·辽宁葫芦岛 高一月考)(多选题)已知函数,的图象分别如图1,2所示,方程,,的实根个数分别为a,b,c,则( )
A. B. C. D.
【答案】AD
【解析】由图,方程,,此时对应4个解,故;
方程,得或者,此时有2个解,故;
方程,取到4个值,如图所示:
即或或或,则对应的的解,有6个,故.
根据选项,可得A,D成立.故选:AD.
8.(多选)(2020·化州市第一中学高二月考)(多选)已知函数,则下列对于的性质表述正确的是( )
A.为偶函数
B.
C.在上的最大值为
D.在区间上至少有一个零点
【答案】ABCD
【解析】因为,所以其的定义域为,
A选项,,所以函数为偶函数,故A正确;
B选项,,故B正确;
C选项,因为,当,单调递增,所以单调递减,因此,故C正确;
D选项,因为,所以,,
即,由零点存在性定理可得:在区间上存在零点,故D正确;故选ABCD
二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
9.(2020·全国高一课时练习)若二次函数的两个零点分别是和,则的值为________.
【答案】
【解析】由于二次函数的两个零点分别是和,由韦达定理得,解得,因此,.故答案为:.
10.(2020·全国高一课时练习)若函数有零点,则实数k的取值范围是________.
【答案】(0,1]
【解析】有零点,即k∈ 而-|x|≤0,0<≤20=1,∴的值域为(0,1].所以k的取值范围是(0,1]故答案为:(0,1]
11.(2020·全国高三(文))若函数的一个零点在区间内,则实数的取值范围是________.
【答案】.
【解析】由条件可知函数在上单调递增,所以,即,解之得.所以实数的取值范围是.
故答案为:
12.(一题双空)(2018·北京海淀 人大附中高三零模(理))已知函数,
①若a=1,f(x)的最小值是_____;
②若f(x)恰好有2个零点,则实数a的取值范围是_____.
【答案】﹣
【解析】(1)由题意,
时,单调递增,,
时,,,
所以时,;
(2)若,则,恰有两个零点0和1,满足题意,
若,则时,无零点,
但时,有两个零点和,满足题意,
当时,则时,是增函数,,有一个零点,
时,由得或,因为只有两个零点,所以,解得,综上,的取值范围是.
三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
13.(2020·浙江高一课时练习)如图,建立平面直角坐标系,轴在地平面上,轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程表示的曲线上,其中与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标不超过多少时,炮弹可以击中它?请说明理由.
【答案】(1)炮的最大射程是10千米.
(2)当不超过6千米时,炮弹可以击中目标.
【解析】(1)令y=0,得kx-(1+k2)x2=0,
由实际意义和题设条件知x>0,k>0,
故x==≤=10,当且仅当k=1时取等号.所以炮的最大射程为10千米.
(2)因为a>0,所以炮弹可击中目标
存在k>0,使3.2=ka-(1+k2)a2成立
关于k的方程a2k2-20ak+a2+64=0有正根
判别式Δ=(-20a)2-4a2(a2+64)≥0
a≤6.
所以当a不超过6(千米)时,可击中目标.
14.(2020·浙江高一单元测试)研究鲑鱼的科学家发现鲑鱼的游速可以表示为函数,单位是,其中x表示鲑鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是8100个单位时,它的游速是多少?
(2)计算一条鲑鱼静止时耗氧量的单位数.
(3)若鲑鱼A的游速大于鲑鱼B的游速,问这两条鲑鱼谁的耗氧量较大?并说明理由.
【答案】(1);(2)一条鲑鱼静止时的耗氧量为100个单位;(3)鲑鱼A的耗氧量较大.
【解析】(1)将代入函数关系式,得,
所以一条鲑鱼的耗氧量是8100个单位时,它的游速是.
(2)令,得,即,则,所以一条鲑鱼静止时的耗氧量为100个单位.
(3)鲑鱼A的耗氧量较大.
理由:由,得,即,则,
所以鲑鱼A的耗氧量较大.
15.(2020·浙江高一课时练习)某企业生产一种机器的固定成本(即固定投入)为0.5万元,但每生产1百台时又需可变成本(即需另增加投入)0.25万元,市场对此商品的需求量为5百台,销售收入(单位:万元)的函数为,其中x是产品生产并售出的数量(单位:百台).
(1)把利润表示为年产量的函数.
(2)年产量为多少时,企业所得利润最大?
(3)年产量为多少时,企业才不亏本(不赔钱)?
【答案】(1);(2)475台;(3)年产量在11台到4800台之间时,企业不亏本.
【解析】(1)设利润为y万元,
得
即
(2)显然当时,企业会获得最大利润,
此时,,
,即年产量为475台时,企业所得利润最大.
(3)要使企业不亏本,则.
即或
得或,即.
即年产量在11台到4800台之间时,企业不亏本.
16.(2020·浙江高一单元测试)甲商店某种商品4月份(30天,4月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如图所示(1),该商品日销售量Q(件)与时间t(天)的函数关系如图(2)所示.
(1)(2)
(1)写出图(1)表示的销售价格与时间的函数关系式,写出图(2)表示的日销售量与时间的函数关系式及日销售金额M(元)与时间的函数关系式.
(2)乙商店销售同一种商品,在4月份采用另一种销售策略,日销售金额N(元)与时间t(天)之间的函数关系式为,试比较4月份每天两商店销售金额的大小关系。
【答案】(1);(2)4月份的前11天甲商店每天的销售金额比乙商店少,以后乙商店每天的销售金额均比甲商店少
【解析】(1)设销售价格与时间之间的函数关系式是,
将(0,15),(30,30)代入得解得
∴.
设日销售量与时间之间的函数关系式为,
将(0,160),(30,40)代入得解得,
∴
故
(2)∵,
∴.
当时,;当时,.
即4月份的前11天甲商店每天的销售金额比乙商店少,以后乙商店每天的销售金额均比甲商店少.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
