第四章 图形的相似 单元复习题(含解析)北师大版九年级数学上册
文档属性
| 名称 | 第四章 图形的相似 单元复习题(含解析)北师大版九年级数学上册 |

|
|
| 格式 | docx | ||
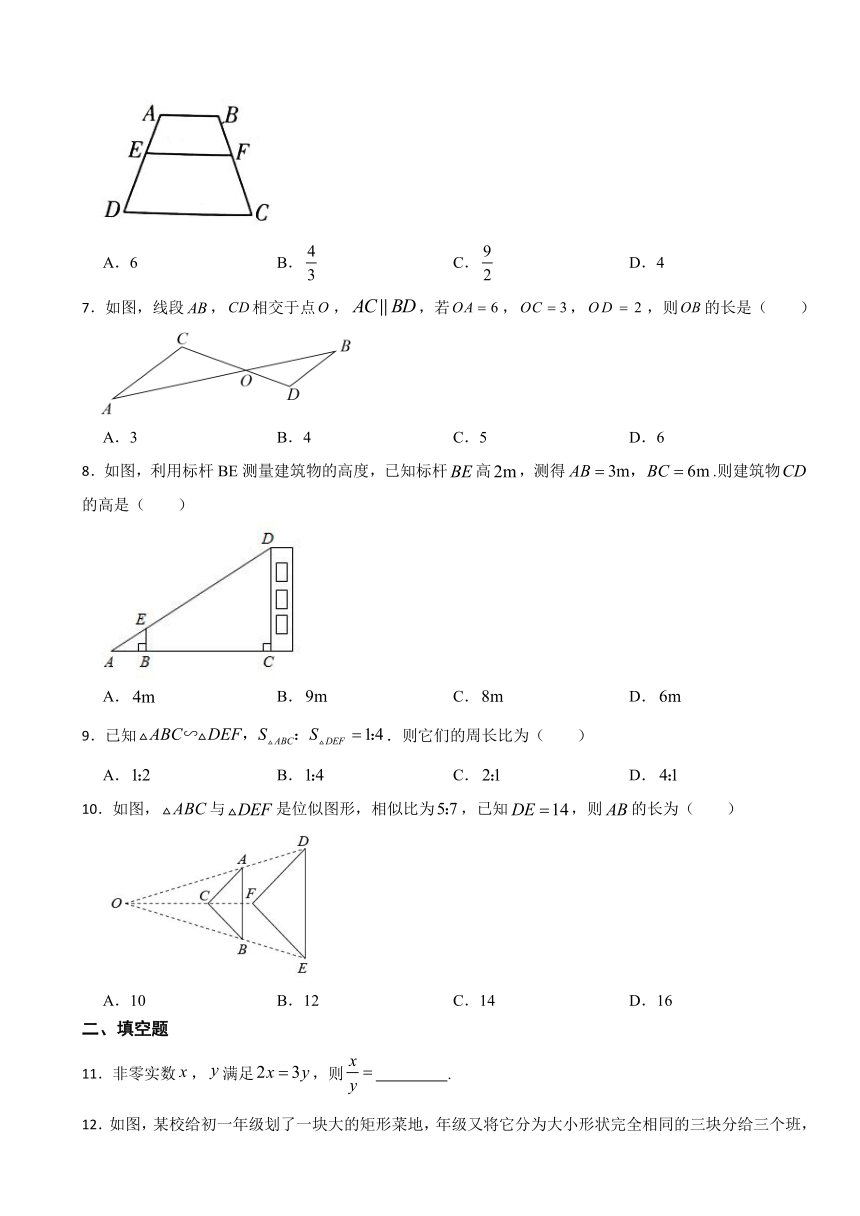
| 文件大小 | 555.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-07 00:00:00 | ||
图片预览



文档简介
北师大版九年级数学上册第四章图形的相似单元复习题
一、选择题
1.若(),则下列比例式成立的是( )
A. B. C. D.
2.已知线段a、b、c,作线段x,使,下列每个图的两条虚线都是平行线,则正确的作法是( )
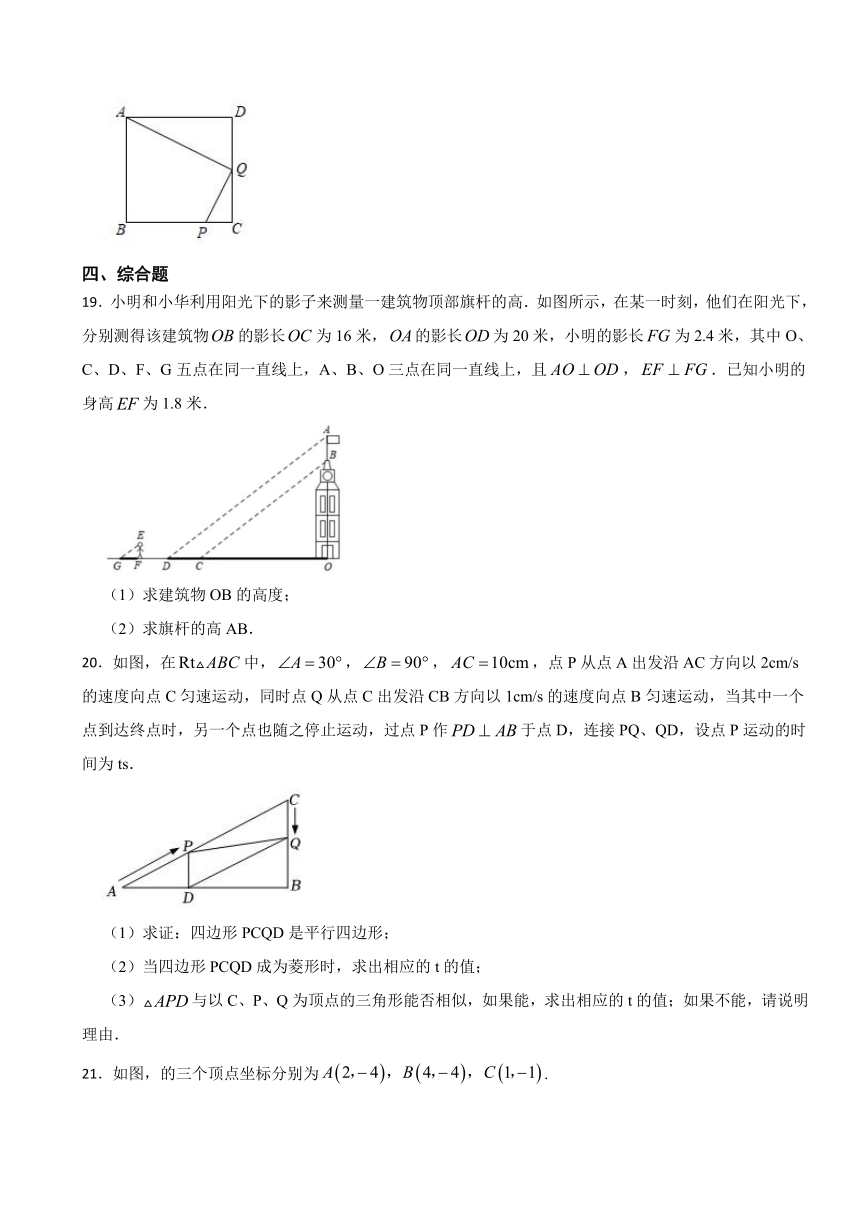
A. B.
C. D.
3.下列说法错误的是( )
A.有一个锐角相等的两个直角三角形相似
B.顶角相等的两个等腰三角形相似
C.任意两个菱形一定相似
D.位似图形一定是相似图形
4.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A.∠AED=∠B B.
C.AD·BC= DE·AC D.DE//BC
5.已知线段,,如果线段c是线段a、b的比例中项,那么c=( )
A.±3 B.3 C.4.5 D.5
6.如图,已知四边形四边形,,,则的长是( ).
A.6 B. C. D.4
7.如图,线段,相交于点,,若,,,则的长是( )
A.3 B.4 C.5 D.6
8.如图,利用标杆BE测量建筑物的高度,已知标杆高,测得.则建筑物的高是( )
A. B. C. D.
9.已知.则它们的周长比为( )
A. B. C. D.
10.如图,与是位似图形,相似比为,已知,则的长为( )
A.10 B.12 C.14 D.16
二、填空题
11.非零实数,满足,则 .
12.如图,某校给初一年级划了一块大的矩形菜地,年级又将它分为大小形状完全相同的三块分给三个班,同学们测量后惊奇的发现,每块小菜地都与原大矩形菜地相似,则原矩形菜地的宽与长之比为 .
13.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为 .
14.如图,正方形与正方形是位似图形,点O为位似中心,相似比为,点D的坐标为,则点B的坐标为 .
三、解答题
15.已知,,求的值.
16.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE//AC、AE//DF,BD:AD=3:2,BF=6,求EF和FC的长.
17.如图,四边形ABCD∽四边形A1B1C1D1,∠A=80°,∠B=75°,∠C=125°,求x,∠D1.
18.如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
四、综合题
19.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物的影长为16米,的影长为20米,小明的影长为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且,.已知小明的身高为1.8米.
(1)求建筑物OB的高度;
(2)求旗杆的高AB.
20.如图,在中,,,,点P从点A出发沿AC方向以2cm/s的速度向点C匀速运动,同时点Q从点C出发沿CB方向以1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,过点P作于点D,连接PQ、QD,设点P运动的时间为ts.
(1)求证:四边形PCQD是平行四边形;
(2)当四边形PCQD成为菱形时,求出相应的t的值;
(3)与以C、P、Q为顶点的三角形能否相似,如果能,求出相应的t的值;如果不能,请说明理由.
21.如图,的三个顶点坐标分别为.
(1)直接写出关于轴对称的三个顶点的坐标;
(2)画出绕点逆时针旋转后的;
(3)以点为位似中心,在网格中画出的位似图形,使与的相似比为.
答案解析部分
1.【答案】A
【解析】【解答】解:A、∵,∴4x=3y,故此选项正确,符合题意;
B、∵,∴3x=4y,故此选项错误,不符合题意;
C、∵,∴3x=4y,故此选项错误,不符合题意;
D、∵,∴xy=12,故此选项错误,不符合题意.
故答案为:A.
【分析】根据比例的性质,两内项之积等于两外项之积,将各个选项中的比例式,变形为等积式,与题干给的等积式进行比较即可判断得出答案.
2.【答案】B
【解析】【解答】解:∵,
∴,
观察选项可知,选项B符合题意,
故答案为:B.
【分析】根据平行线分线段成比例的性质进行判断即可.
3.【答案】C
【解析】【解答】解:A、根据两角对应相等的两个三角形相似可知,有一个锐角相等的两个直角三角形相似,不符合题意;
B、顶角相等的两个等腰三角形,它们的底角也相等,故这两个三角形相似,不符合题意;
C、∵两个菱形的对应角不一定相等,
∴两个菱形不一定相似,符合题意;
D、位似图形一定是相似图形,不符合题意;
故答案为:C.
【分析】根据相似图形的判定方法求解即可。
4.【答案】C
【解析】【解答】解:A、∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,故A不符合题意;
B、∵,∠A=∠A,
∴△ADE∽△ACB,故B不符合题意;
C、∵AD·BC= DE·AC,
∴,
而无夹角相等,
∴不能判定△ADE∽△ACB,故C符合题意;
D、∵DE//BC,
∴△ADE∽△ACB,故D不符合题意;
故答案为:C.
【分析】根据有两组角对应相等的两个三角形相似可判断A选项;根据有两组边成比例且夹角相等的两个三角形相似可判断B、C;根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似可判断D.
5.【答案】B
【解析】【解答】解:根据比例中项的概念结合比例的基本性质,得:
比例中项的平方等于两条线段的乘积.
则,
解得(线段是正数,负值舍去),
所以.
故答案为:B.
【分析】根据线段c是线段a、b的比例中项可得c2=ab,代入求解即可.
6.【答案】C
【解析】【解答】解:∵四边形四边形,
∴,
∵,,
∴,
故答案为:C.
【分析】由相似多边形的对应边成比例即可求解.
7.【答案】B
【解析】【解答】解:∵,
∴,
∴,
∵,,,
∴,
解得:,
故答案为:B.
【分析】易证△AOC∽△BOD,然后根据相似三角形的对应边成比例进行计算.
8.【答案】D
【解析】【解答】解:∵,
∴,
∴,
∵高,,
∴,
∴,
故答案为:D.
【分析】易证△AEB∽△ADC,然后将已知数据代入进行计算.
9.【答案】A
【解析】【解答】解:∵,
∴△ABC与△DEF的相似比是,
∴它们的周长比为.
故答案为:A.
【分析】根据相似三角形的性质:相似三角形的周长之比等于相似比求解即可。
10.【答案】A
【解析】【解答】解:∵与是位似图形,相似比为,,
∴
∴,
故答案为:A.
【分析】根据位似图形的相似比等于对应边的比进行解答.
11.【答案】
【解析】【解答】解:∵,
∴,
故答案为:.
【分析】根据比例的性质:两内项之积等于两外项之积,将等积式改为比例式即可.
12.【答案】
【解析】【解答】解:设原矩形的长为x,宽为y,
∵年级又将它分为大小形状完全相同的三块分给三个班,
∴小矩形的长为y,宽为x
∵ 每块小菜地都与原大矩形菜地相似 ,
∴
解之:,
∴.
故答案为:
【分析】设原矩形的长为x,宽为y,可表示出最小的矩形的长和宽,再根据每块小菜地都与原大矩形菜地相似 ,可得到对应边成比例,即可表示出x的值,然后求出y与x的比值即可.
13.【答案】16cm
【解析】【解答】解:∵△ABC∽△A′B′C′,且,即相似三角形的相似比为,
∵△ABC的周长为12cm
∴△A′B′C′的周长为12÷=16cm.
故答案为:16cm.
【分析】根据相似三角形的周长比等于相似比进行计算.
14.【答案】
【解析】【解答】解:∵正方形与正方形是位似图形,点O是位似中心,相似比为,点D的坐标为,
∴,则,
∴点B的坐标是:.
故答案为:.
【分析】根据相似三角形的性质可得,则,即可得到点B的坐标为。
15.【答案】解:
设,,
将,,代入
得,解得
,,
故答案为:2
【解析】【分析】设,,,再结合可得,求出,最后求出a、b、c的值并代入计算即可。
16.【答案】解:,
,即,
,
,
,
,即,
,
.
【解析】【分析】根据平行线分线段成比例的性质可得,即,求出,求出BE的长,再根据,即,求出,最后利用线段的和差求出CF的长即可。
17.【答案】解:∵,
∴.
∵四边形 四边形,
∴,,
即.
∴.
【解析】【分析】根据四边形内角和为360°可得∠D=80°,由相似图形的性质可得∠D1=∠D,,据此求解.
18.【答案】证明:∵四边形是正方形
∴,
∵
∴
∵是的中点
∴
∵,
∴
∵
∴.
【解析】【分析】先证明,再结合,可得。
19.【答案】(1)解:根据题意得:,
∴,
,
∴,
∴,即,
∴米
(2)解:根据题意得:,
∴,
,
∴,
∴,即,
∴米,
由(1)得米,
∴(米),
∴旗杆的高是米.
【解析】【分析】(1)证明, 利用相似三角形的对应边成比例即可求解;
(2) 证明, 可得,据此求出AO的长,利用AB=AO-BO即可求解.
20.【答案】(1)证明:由题意,,
∵,
∴
∴
∵,
∴
∴四边形PCQD是平行四边形.
(2)解:四边形PCQD是菱形,则
∵,
∴
∴
∴
∴当四边形PCQD是菱形时,
(3)解:由题意,,,
当时,
即,解得
当,
即,解得
∴当或时,与以C、P、Q为顶点的三角形相似.
【解析】【分析】(1)由题意可得AP=2t,CQ=t,根据含30°角的直角三角形的性质可得PD=AP=t,则CQ=PD,根据垂直于同一直线的两直线互相平行可得PD∥CQ,然后根据平行四边形的判定定理进行证明;
(2)由菱形的性质可得PC=CQ,由题意可得PC=10-2t,CQ=t,据此可得t的值;
(3)由题意可得∠APD=∠C,AP=2t,PD=CQ=t,PC=10-2t,然后分△APD∽△PCQ、△APD∽△QCP,根据相似三角形的对应边成比例可得t的值.
21.【答案】(1)解:
(2)解:绕点逆时针旋转,如图所示,
即为所求图形的位置.
(3)解:∵,,,点为位似中心,相似比为,即位似比为,
∴,,,
∴延长到,使得,即,延长到,使得,即,连接,,得;
反向延长到,使得,即,反向延长到,使得,即,连接,,得,如图所示,
∴点为位似中心,相似比为,,都是所求图形.
【解析】【解答】解:(1)关于轴对称的三个顶点的坐标,横坐标变为原来的相反数,纵坐标不变,,
∴.
【分析】(1)关于y轴对称的点:横坐标互为相反数,纵坐标相同,据此不难得到点A1、B1、C1的坐标;
(2)根据旋转的性质,分别将点A、B、C绕点O逆时针旋转90°得到点A2、B2、C2,然后顺次连接即可;
(3)分别延长AB、CB,或反向延长BA、BC,使A3B=2AB,C3B=2CB,然后顺次连接即可.
一、选择题
1.若(),则下列比例式成立的是( )
A. B. C. D.
2.已知线段a、b、c,作线段x,使,下列每个图的两条虚线都是平行线,则正确的作法是( )
A. B.
C. D.
3.下列说法错误的是( )
A.有一个锐角相等的两个直角三角形相似
B.顶角相等的两个等腰三角形相似
C.任意两个菱形一定相似
D.位似图形一定是相似图形
4.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件不能满足△ADE∽△ACB的条件是( )
A.∠AED=∠B B.
C.AD·BC= DE·AC D.DE//BC
5.已知线段,,如果线段c是线段a、b的比例中项,那么c=( )
A.±3 B.3 C.4.5 D.5
6.如图,已知四边形四边形,,,则的长是( ).
A.6 B. C. D.4
7.如图,线段,相交于点,,若,,,则的长是( )
A.3 B.4 C.5 D.6
8.如图,利用标杆BE测量建筑物的高度,已知标杆高,测得.则建筑物的高是( )
A. B. C. D.
9.已知.则它们的周长比为( )
A. B. C. D.
10.如图,与是位似图形,相似比为,已知,则的长为( )
A.10 B.12 C.14 D.16
二、填空题
11.非零实数,满足,则 .
12.如图,某校给初一年级划了一块大的矩形菜地,年级又将它分为大小形状完全相同的三块分给三个班,同学们测量后惊奇的发现,每块小菜地都与原大矩形菜地相似,则原矩形菜地的宽与长之比为 .
13.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为 .
14.如图,正方形与正方形是位似图形,点O为位似中心,相似比为,点D的坐标为,则点B的坐标为 .
三、解答题
15.已知,,求的值.
16.如图,在△ABC中,D、E、F分别是AB、BC上的点,且DE//AC、AE//DF,BD:AD=3:2,BF=6,求EF和FC的长.
17.如图,四边形ABCD∽四边形A1B1C1D1,∠A=80°,∠B=75°,∠C=125°,求x,∠D1.
18.如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
四、综合题
19.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物的影长为16米,的影长为20米,小明的影长为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且,.已知小明的身高为1.8米.
(1)求建筑物OB的高度;
(2)求旗杆的高AB.
20.如图,在中,,,,点P从点A出发沿AC方向以2cm/s的速度向点C匀速运动,同时点Q从点C出发沿CB方向以1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,过点P作于点D,连接PQ、QD,设点P运动的时间为ts.
(1)求证:四边形PCQD是平行四边形;
(2)当四边形PCQD成为菱形时,求出相应的t的值;
(3)与以C、P、Q为顶点的三角形能否相似,如果能,求出相应的t的值;如果不能,请说明理由.
21.如图,的三个顶点坐标分别为.
(1)直接写出关于轴对称的三个顶点的坐标;
(2)画出绕点逆时针旋转后的;
(3)以点为位似中心,在网格中画出的位似图形,使与的相似比为.
答案解析部分
1.【答案】A
【解析】【解答】解:A、∵,∴4x=3y,故此选项正确,符合题意;
B、∵,∴3x=4y,故此选项错误,不符合题意;
C、∵,∴3x=4y,故此选项错误,不符合题意;
D、∵,∴xy=12,故此选项错误,不符合题意.
故答案为:A.
【分析】根据比例的性质,两内项之积等于两外项之积,将各个选项中的比例式,变形为等积式,与题干给的等积式进行比较即可判断得出答案.
2.【答案】B
【解析】【解答】解:∵,
∴,
观察选项可知,选项B符合题意,
故答案为:B.
【分析】根据平行线分线段成比例的性质进行判断即可.
3.【答案】C
【解析】【解答】解:A、根据两角对应相等的两个三角形相似可知,有一个锐角相等的两个直角三角形相似,不符合题意;
B、顶角相等的两个等腰三角形,它们的底角也相等,故这两个三角形相似,不符合题意;
C、∵两个菱形的对应角不一定相等,
∴两个菱形不一定相似,符合题意;
D、位似图形一定是相似图形,不符合题意;
故答案为:C.
【分析】根据相似图形的判定方法求解即可。
4.【答案】C
【解析】【解答】解:A、∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,故A不符合题意;
B、∵,∠A=∠A,
∴△ADE∽△ACB,故B不符合题意;
C、∵AD·BC= DE·AC,
∴,
而无夹角相等,
∴不能判定△ADE∽△ACB,故C符合题意;
D、∵DE//BC,
∴△ADE∽△ACB,故D不符合题意;
故答案为:C.
【分析】根据有两组角对应相等的两个三角形相似可判断A选项;根据有两组边成比例且夹角相等的两个三角形相似可判断B、C;根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似可判断D.
5.【答案】B
【解析】【解答】解:根据比例中项的概念结合比例的基本性质,得:
比例中项的平方等于两条线段的乘积.
则,
解得(线段是正数,负值舍去),
所以.
故答案为:B.
【分析】根据线段c是线段a、b的比例中项可得c2=ab,代入求解即可.
6.【答案】C
【解析】【解答】解:∵四边形四边形,
∴,
∵,,
∴,
故答案为:C.
【分析】由相似多边形的对应边成比例即可求解.
7.【答案】B
【解析】【解答】解:∵,
∴,
∴,
∵,,,
∴,
解得:,
故答案为:B.
【分析】易证△AOC∽△BOD,然后根据相似三角形的对应边成比例进行计算.
8.【答案】D
【解析】【解答】解:∵,
∴,
∴,
∵高,,
∴,
∴,
故答案为:D.
【分析】易证△AEB∽△ADC,然后将已知数据代入进行计算.
9.【答案】A
【解析】【解答】解:∵,
∴△ABC与△DEF的相似比是,
∴它们的周长比为.
故答案为:A.
【分析】根据相似三角形的性质:相似三角形的周长之比等于相似比求解即可。
10.【答案】A
【解析】【解答】解:∵与是位似图形,相似比为,,
∴
∴,
故答案为:A.
【分析】根据位似图形的相似比等于对应边的比进行解答.
11.【答案】
【解析】【解答】解:∵,
∴,
故答案为:.
【分析】根据比例的性质:两内项之积等于两外项之积,将等积式改为比例式即可.
12.【答案】
【解析】【解答】解:设原矩形的长为x,宽为y,
∵年级又将它分为大小形状完全相同的三块分给三个班,
∴小矩形的长为y,宽为x
∵ 每块小菜地都与原大矩形菜地相似 ,
∴
解之:,
∴.
故答案为:
【分析】设原矩形的长为x,宽为y,可表示出最小的矩形的长和宽,再根据每块小菜地都与原大矩形菜地相似 ,可得到对应边成比例,即可表示出x的值,然后求出y与x的比值即可.
13.【答案】16cm
【解析】【解答】解:∵△ABC∽△A′B′C′,且,即相似三角形的相似比为,
∵△ABC的周长为12cm
∴△A′B′C′的周长为12÷=16cm.
故答案为:16cm.
【分析】根据相似三角形的周长比等于相似比进行计算.
14.【答案】
【解析】【解答】解:∵正方形与正方形是位似图形,点O是位似中心,相似比为,点D的坐标为,
∴,则,
∴点B的坐标是:.
故答案为:.
【分析】根据相似三角形的性质可得,则,即可得到点B的坐标为。
15.【答案】解:
设,,
将,,代入
得,解得
,,
故答案为:2
【解析】【分析】设,,,再结合可得,求出,最后求出a、b、c的值并代入计算即可。
16.【答案】解:,
,即,
,
,
,
,即,
,
.
【解析】【分析】根据平行线分线段成比例的性质可得,即,求出,求出BE的长,再根据,即,求出,最后利用线段的和差求出CF的长即可。
17.【答案】解:∵,
∴.
∵四边形 四边形,
∴,,
即.
∴.
【解析】【分析】根据四边形内角和为360°可得∠D=80°,由相似图形的性质可得∠D1=∠D,,据此求解.
18.【答案】证明:∵四边形是正方形
∴,
∵
∴
∵是的中点
∴
∵,
∴
∵
∴.
【解析】【分析】先证明,再结合,可得。
19.【答案】(1)解:根据题意得:,
∴,
,
∴,
∴,即,
∴米
(2)解:根据题意得:,
∴,
,
∴,
∴,即,
∴米,
由(1)得米,
∴(米),
∴旗杆的高是米.
【解析】【分析】(1)证明, 利用相似三角形的对应边成比例即可求解;
(2) 证明, 可得,据此求出AO的长,利用AB=AO-BO即可求解.
20.【答案】(1)证明:由题意,,
∵,
∴
∴
∵,
∴
∴四边形PCQD是平行四边形.
(2)解:四边形PCQD是菱形,则
∵,
∴
∴
∴
∴当四边形PCQD是菱形时,
(3)解:由题意,,,
当时,
即,解得
当,
即,解得
∴当或时,与以C、P、Q为顶点的三角形相似.
【解析】【分析】(1)由题意可得AP=2t,CQ=t,根据含30°角的直角三角形的性质可得PD=AP=t,则CQ=PD,根据垂直于同一直线的两直线互相平行可得PD∥CQ,然后根据平行四边形的判定定理进行证明;
(2)由菱形的性质可得PC=CQ,由题意可得PC=10-2t,CQ=t,据此可得t的值;
(3)由题意可得∠APD=∠C,AP=2t,PD=CQ=t,PC=10-2t,然后分△APD∽△PCQ、△APD∽△QCP,根据相似三角形的对应边成比例可得t的值.
21.【答案】(1)解:
(2)解:绕点逆时针旋转,如图所示,
即为所求图形的位置.
(3)解:∵,,,点为位似中心,相似比为,即位似比为,
∴,,,
∴延长到,使得,即,延长到,使得,即,连接,,得;
反向延长到,使得,即,反向延长到,使得,即,连接,,得,如图所示,
∴点为位似中心,相似比为,,都是所求图形.
【解析】【解答】解:(1)关于轴对称的三个顶点的坐标,横坐标变为原来的相反数,纵坐标不变,,
∴.
【分析】(1)关于y轴对称的点:横坐标互为相反数,纵坐标相同,据此不难得到点A1、B1、C1的坐标;
(2)根据旋转的性质,分别将点A、B、C绕点O逆时针旋转90°得到点A2、B2、C2,然后顺次连接即可;
(3)分别延长AB、CB,或反向延长BA、BC,使A3B=2AB,C3B=2CB,然后顺次连接即可.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
