图形的相似[下学期]
图片预览





文档简介
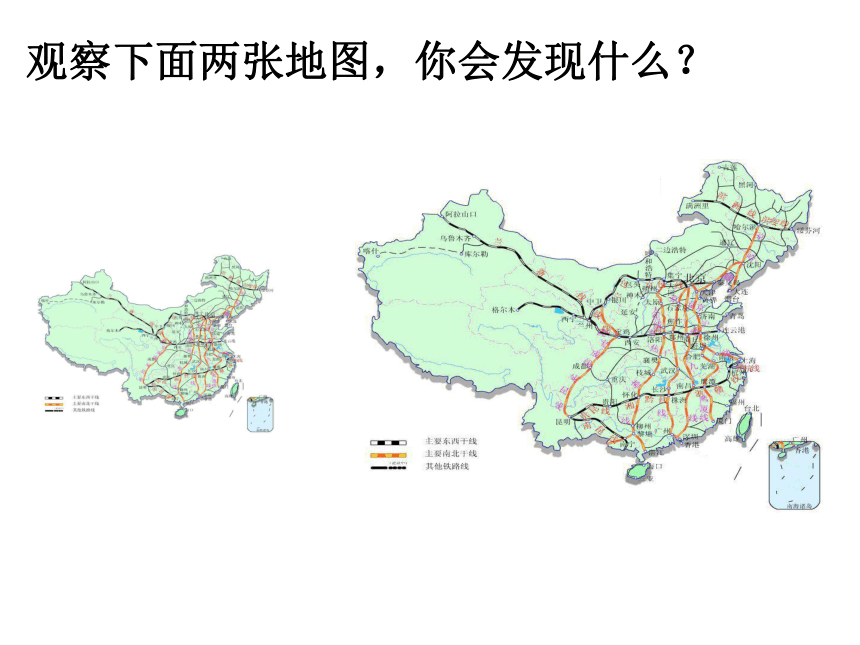
课件33张PPT。 图形的相似 图形的相似 图形的相似 图形的相似 图形的相似观察下面两张地图,你会发现什么?想一想:我们刚才所看到的两副图形有什么相同点和不同点?相同点: 形状相同.
不同点: 大小不一定相同.满足以上两个条件即形状相同,大小不一定相同的图形相似图形请列举生活中相似图形的例子! 说一说 同一底片印出来的不同尺寸的照片也是相似图形. 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。 放电影时胶片上的图像和它映射到屏幕上的图像,都是彼此相似的.思考:
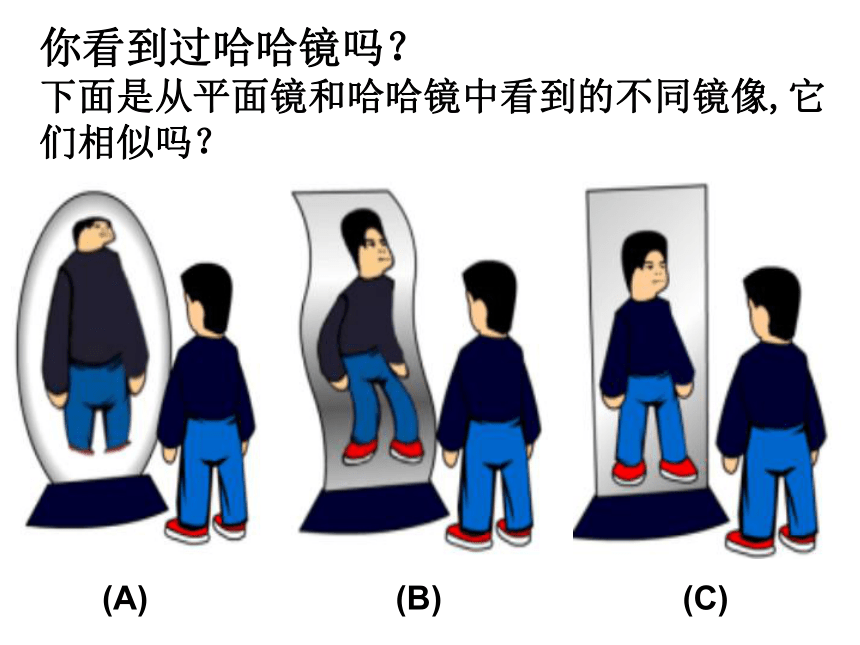
相似图形与全等图形的关系怎样呢?你看到过哈哈镜吗?
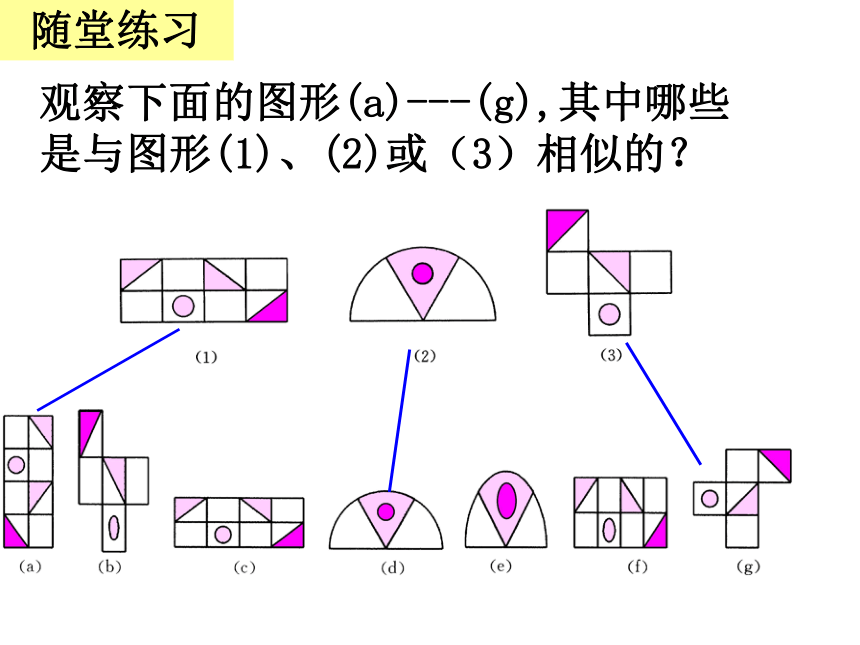
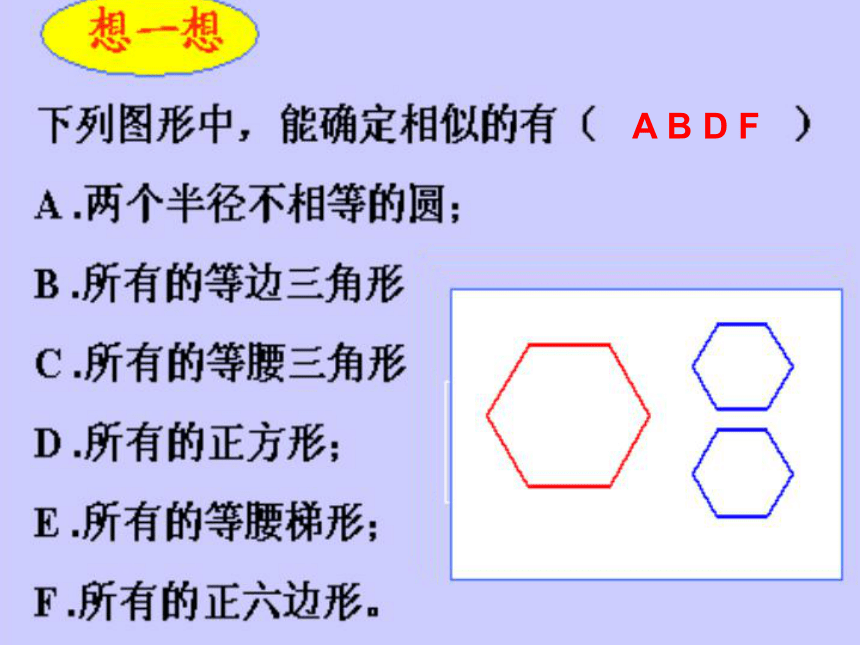
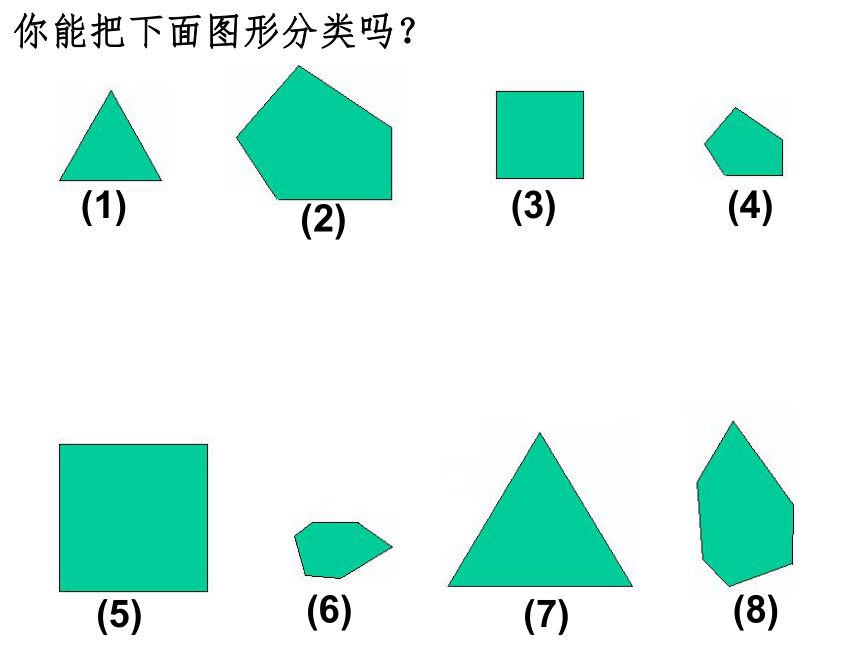
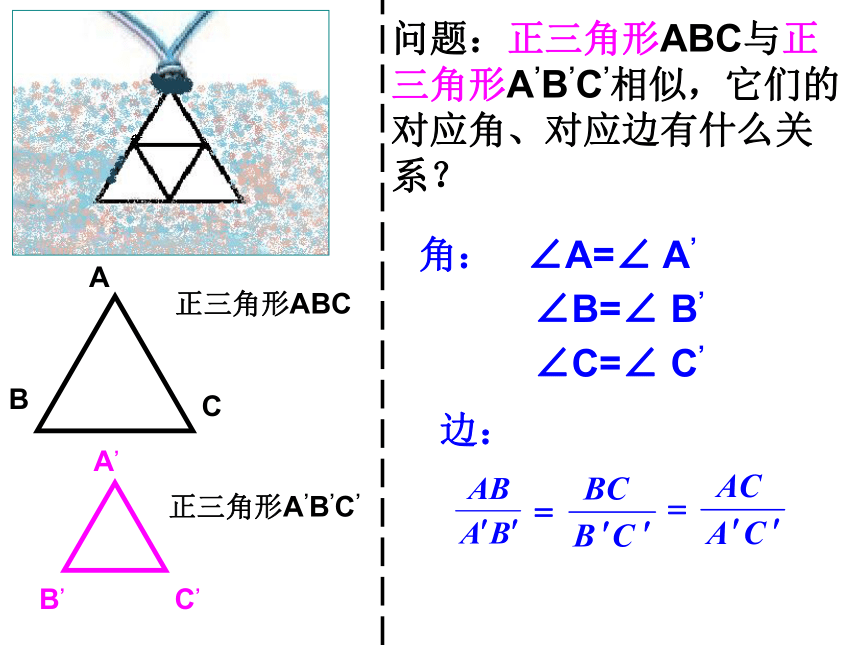
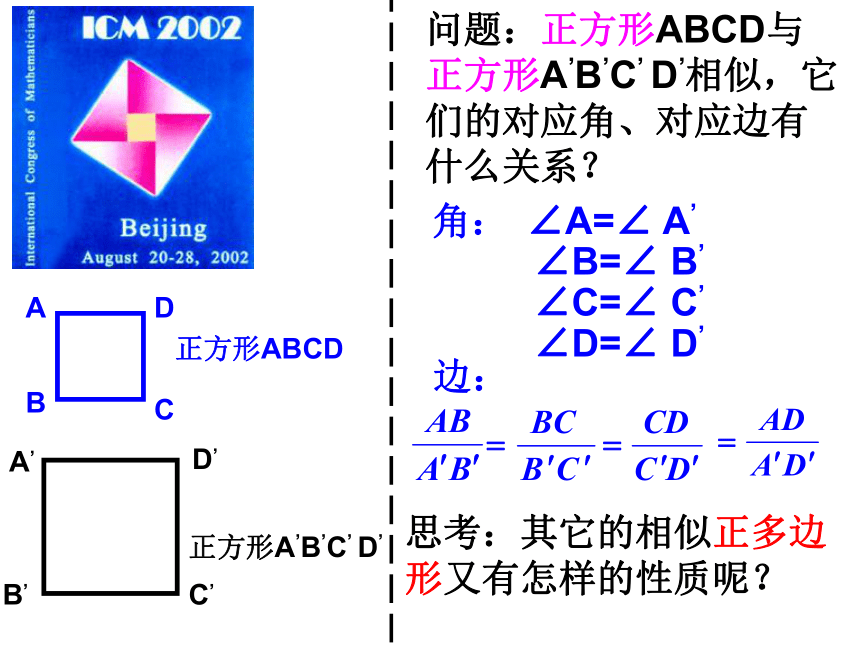
下面是从平面镜和哈哈镜中看到的不同镜像,它们相似吗?(A)(B)(C)观察下面的图形(a)---(g),其中哪些是与图形(1)、(2)或(3)相似的?随堂练习A B D F(1)(2)(3)(4)(7)(8)你能把下面图形分类吗?(5)(6)相似多边形相似多边形相似多边形正三角形ABC正三角形A,B,C,问题:正三角形ABC与正三角形A,B,C,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:正方形ABCD正方形A,B,C, D,问题:正方形ABCD与正方形A,B,C, D,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:∠D=∠ D,思考:其它的相似正多边形又有怎样的性质呢?问题:这两 个相似四边形对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:∠D=∠ D,探究 新知..EE,思考:你认为两个相似多边形对应角、对应边有什么关系?相似多边形的性质:相似多边形对应角相等,对应边的比相等相似多边形对应边的比称为相似比
记作:k? 新知思考:相似比为1时,相似的两个图形有什么关系?? 新知全等图形是一种特殊的相似图形应用相似多边形的性质解决问题:1、如图,△ABC与△ A,B,C, 相似,
则∠B,= ;
BC= ;
△ABC与△ A,B,C, 相似比为 。应用新知72°404︰1△ A,B,C, 与△ABC相似比为 。1︰4应用相似多边形的性质解决问题:2、如图,四边形ABCD与EFGH相似,求角α、β的大小和EH的长度x解:∵四边形ABCD与EFGH相似∴∠α=∠C=83°∠A=∠E=118°在四边形ABCD中∠β=360°-(78°+83°+118°)=81°又∵∴解得:x=28cm应用新知 所有的等腰直角三角形都相似吗?利用你手中的等腰直角三角形观察内外两个三角形的边角有什么关系?81145.5abcdBAFEDC比例线段 对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即
那么这四条线段叫做成比例线段,简称比例线段。判断下列各组长度的线段是否成比例?
(1) 1厘米,2厘米,2厘米,4厘米;
(2) 2厘米,10厘米,4厘米,5厘米;
(3) 2厘米,3厘米,4厘米,5厘米。
随堂练习问题:现有一长为30cm,宽为15cm的矩形奔马图,在其四周表上宽为2cm的木质边框。那么内外边缘所成的矩形相似吗?2
cm2cm2cm2
cm探究 新知30cm15cm34cm19cm∵∴内外边缘所成的矩形不相似。? 新知相似多边形的判定(定义法)如果两个多边形对应角相等,对应边的比相等,那么这两个多边形相似。思考1:如果两个多边形角对应相等,那么它们相似吗?为什么?请举例说明。正方形矩形思考2:如果两个多边形对应边的比相等,那么它们相似吗?为什么?请举例说明。正方形菱形两个多边形相似对应角相等对应边的比相等答:不一定相似。因为虽然它们对应边是成比例的,但它们的对应角不一定相等。答:不一定相似。因为虽然它们对应角相等,但它们对应边不一定成比例。问题:现有一长为30cm,宽为15cm的矩形奔马图,请动手设计边框,使所得内外边缘所成的矩形相似。动手 设计应用相似多边形的判定解决问题:1、如图所示的两个三角形相似吗?为什么?解:∵∠A=∠D=90°∠B=∠E=45°∠C=∠F=45°在Rt△ABC中BC=在Rt△DEF中EF=∴两个三角形相似应用新知注意:要比较所有对应角与对应边的比。
应用相似多边形的判定解决问题:2、如图所示的两个四边形相似吗?为什么?解:∴两个四边形不相似变式:若EH=60,那么这两个四边形相似吗?60应用新知注意:举出一组对应角或对应边的比不相等即可说明不相似。思维的发散与创新1、已知A4纸的宽度为21cm,如图将其对折后,所得的矩形都和原来的矩形相似,求A4纸的长度。
A421cm对折x0.5x21cm对折0.5x10.5cm解:∵对折后矩形和原来的矩形相似∴解得:思维的发散与创新变式:若一张矩形的纸片沿较长边的中点对折,如果得到的两个矩形和原来矩形相似,那么原来的矩形的长宽比是多少?
对折a0.5ab对折0.5a0.5bb解:∵对折后矩形和原来的矩形相似∴∴∴喜谈收获相似多边形性质作业:同步训练ABCDA,B,C, D,数据记录:∠A=∠A,=∠B=∠B,=∠C=∠C,=∠D=∠D,=AB=C,D,=AD=B,C,=CD=BC=A,B,=A,D,=发现:发现:应用相似多边形的性质解决问题:3、如图,五边形ABCDE和FMNPQ相似,求未知数x,y,z的长度和角α,β的大小。E应用新知
不同点: 大小不一定相同.满足以上两个条件即形状相同,大小不一定相同的图形相似图形请列举生活中相似图形的例子! 说一说 同一底片印出来的不同尺寸的照片也是相似图形. 两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。 放电影时胶片上的图像和它映射到屏幕上的图像,都是彼此相似的.思考:
相似图形与全等图形的关系怎样呢?你看到过哈哈镜吗?
下面是从平面镜和哈哈镜中看到的不同镜像,它们相似吗?(A)(B)(C)观察下面的图形(a)---(g),其中哪些是与图形(1)、(2)或(3)相似的?随堂练习A B D F(1)(2)(3)(4)(7)(8)你能把下面图形分类吗?(5)(6)相似多边形相似多边形相似多边形正三角形ABC正三角形A,B,C,问题:正三角形ABC与正三角形A,B,C,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:正方形ABCD正方形A,B,C, D,问题:正方形ABCD与正方形A,B,C, D,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:∠D=∠ D,思考:其它的相似正多边形又有怎样的性质呢?问题:这两 个相似四边形对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:∠D=∠ D,探究 新知..EE,思考:你认为两个相似多边形对应角、对应边有什么关系?相似多边形的性质:相似多边形对应角相等,对应边的比相等相似多边形对应边的比称为相似比
记作:k? 新知思考:相似比为1时,相似的两个图形有什么关系?? 新知全等图形是一种特殊的相似图形应用相似多边形的性质解决问题:1、如图,△ABC与△ A,B,C, 相似,
则∠B,= ;
BC= ;
△ABC与△ A,B,C, 相似比为 。应用新知72°404︰1△ A,B,C, 与△ABC相似比为 。1︰4应用相似多边形的性质解决问题:2、如图,四边形ABCD与EFGH相似,求角α、β的大小和EH的长度x解:∵四边形ABCD与EFGH相似∴∠α=∠C=83°∠A=∠E=118°在四边形ABCD中∠β=360°-(78°+83°+118°)=81°又∵∴解得:x=28cm应用新知 所有的等腰直角三角形都相似吗?利用你手中的等腰直角三角形观察内外两个三角形的边角有什么关系?81145.5abcdBAFEDC比例线段 对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即
那么这四条线段叫做成比例线段,简称比例线段。判断下列各组长度的线段是否成比例?
(1) 1厘米,2厘米,2厘米,4厘米;
(2) 2厘米,10厘米,4厘米,5厘米;
(3) 2厘米,3厘米,4厘米,5厘米。
随堂练习问题:现有一长为30cm,宽为15cm的矩形奔马图,在其四周表上宽为2cm的木质边框。那么内外边缘所成的矩形相似吗?2
cm2cm2cm2
cm探究 新知30cm15cm34cm19cm∵∴内外边缘所成的矩形不相似。? 新知相似多边形的判定(定义法)如果两个多边形对应角相等,对应边的比相等,那么这两个多边形相似。思考1:如果两个多边形角对应相等,那么它们相似吗?为什么?请举例说明。正方形矩形思考2:如果两个多边形对应边的比相等,那么它们相似吗?为什么?请举例说明。正方形菱形两个多边形相似对应角相等对应边的比相等答:不一定相似。因为虽然它们对应边是成比例的,但它们的对应角不一定相等。答:不一定相似。因为虽然它们对应角相等,但它们对应边不一定成比例。问题:现有一长为30cm,宽为15cm的矩形奔马图,请动手设计边框,使所得内外边缘所成的矩形相似。动手 设计应用相似多边形的判定解决问题:1、如图所示的两个三角形相似吗?为什么?解:∵∠A=∠D=90°∠B=∠E=45°∠C=∠F=45°在Rt△ABC中BC=在Rt△DEF中EF=∴两个三角形相似应用新知注意:要比较所有对应角与对应边的比。
应用相似多边形的判定解决问题:2、如图所示的两个四边形相似吗?为什么?解:∴两个四边形不相似变式:若EH=60,那么这两个四边形相似吗?60应用新知注意:举出一组对应角或对应边的比不相等即可说明不相似。思维的发散与创新1、已知A4纸的宽度为21cm,如图将其对折后,所得的矩形都和原来的矩形相似,求A4纸的长度。
A421cm对折x0.5x21cm对折0.5x10.5cm解:∵对折后矩形和原来的矩形相似∴解得:思维的发散与创新变式:若一张矩形的纸片沿较长边的中点对折,如果得到的两个矩形和原来矩形相似,那么原来的矩形的长宽比是多少?
对折a0.5ab对折0.5a0.5bb解:∵对折后矩形和原来的矩形相似∴∴∴喜谈收获相似多边形性质作业:同步训练ABCDA,B,C, D,数据记录:∠A=∠A,=∠B=∠B,=∠C=∠C,=∠D=∠D,=AB=C,D,=AD=B,C,=CD=BC=A,B,=A,D,=发现:发现:应用相似多边形的性质解决问题:3、如图,五边形ABCDE和FMNPQ相似,求未知数x,y,z的长度和角α,β的大小。E应用新知
