切线的性质和判定[上学期]
文档属性
| 名称 | 切线的性质和判定[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 276.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-14 00:00:00 | ||
图片预览





文档简介
课件22张PPT。—— 切线长定理24.2.2直线与圆的位置关系(3)学无止境迎难而上1.切线的判定定理:经过半径的外端并且垂直于这条半径的
直线是圆的切线.2.切线的性质定理:圆的切线垂直于过切点的半径温故而知新探究:如图:PA为⊙O的一条切线,沿着直线PO将图形对折,设圆上与点A重合的点为B,这时OB是⊙O一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性说明图中的PA与PB,∠APO与∠BPO有什么关系?PABOOB也是的⊙O半径,PB也是切线,
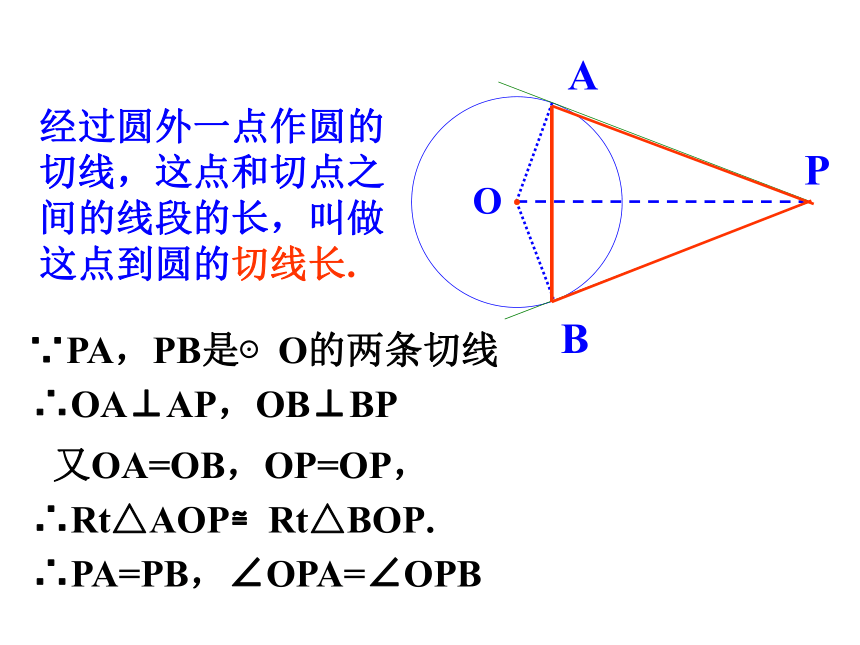
PA=PB ,∠APO=∠BPO ,ABPO经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.∵PA,PB是⊙O的两条切线∴OA⊥AP,OB⊥BP又OA=OB,OP=OP,∴Rt△AOP≌Rt△BOP.∴PA=PB,∠OPA=∠OPB切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.平分切点所成的两弧,垂直平分切点所成的弦.已知,如图,PA、PB是⊙O的两条切线,
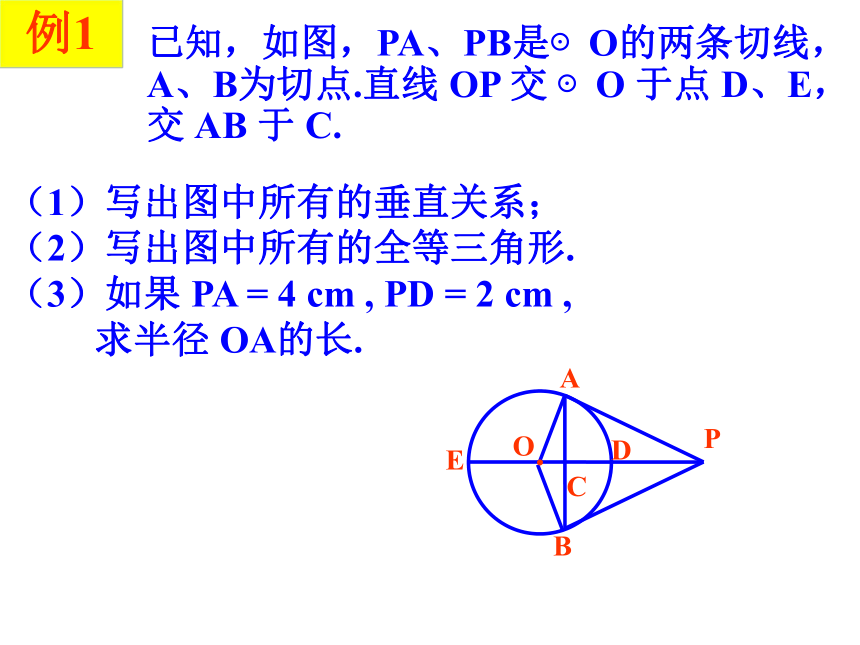
A、B为切点.直线 OP 交 ⊙O 于点 D、E,
交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形.
(3)如果 PA = 4 cm , PD = 2 cm ,
求半径 OA的长.例1例1解:(1) OA⊥PA , OB⊥PB , OP⊥AB(2) △OAP ≌△ OBP , △OCA≌△OCB ,
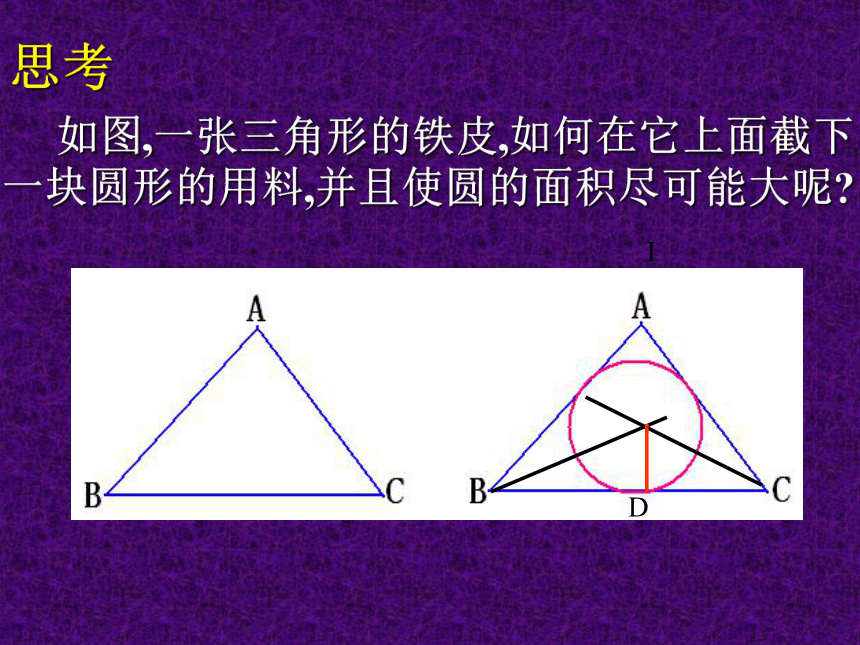
△ACP≌△BCP.(3) 设 OA = x cm , 则 PO = PD + x = (2 + x )cm 在 Rt△OAP 中,由勾股定理,得 PA 2 + OA 2 = OP 2 即 4 2 + x 2 = (x + 2 ) 2 解得 x = 3 所以,半径 OA 的长为 3 cm. 思考 如图,一张三角形的铁皮,如何在它上面截下
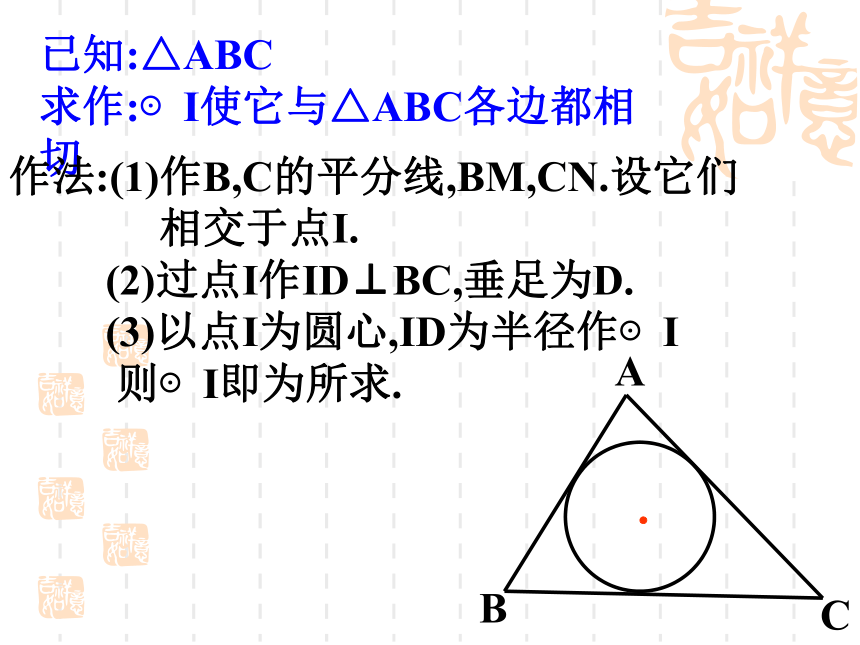
一块圆形的用料,并且使圆的面积尽可能大呢?ID已知:△ABC
求作:⊙I使它与△ABC各边都相切作法:(1)作B,C的平分线,BM,CN.设它们
相交于点I.
(2)过点I作ID⊥BC,垂足为D.
(3)以点I为圆心,ID为半径作⊙I
则⊙I即为所求.内切圆和内心的定义:与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫
做三角形的内心.
这个三角形叫做圆的
外切三角形有关概念例2 △ABC的内切圆⊙O与BC、CA、AB分别相切
于点D、E、F,且AB=9cm,BC=14cm,
CA=13cm,求AF、BD、CE的长.解:设AF=x(cm),则AE=x(cm)∴CD=CE=AC-AE=13-x
BD=BF=AB-AF=9-x由 BD+CD=BC可得
(13-x)+(9-x)=14解得 x=4∴ AF=4(cm), BD=5(cm), CE=9(cm).练习:P106:1.2作业:P110:5,11,12记忆:1. Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.11.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.基础题:1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.EFHG正方形22cm2cm4.已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.∠CAE=∠BAB⊥FE∠BAC+∠CAE=90°H5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.1、已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,以腰DC的中点 E 为圆心的圆与 AB 相切,梯形的上底 AD 与底 BC 是方程 x 2-10x + 16 = 0 的两根,求 ⊙E 的半径 r .F想一想:圆的外切四边形的两组对边有什么关系?说明你的结论的正确性.ABCDOLMNP谢谢大家的合作!
祝大家学习进步,万事如意!
直线是圆的切线.2.切线的性质定理:圆的切线垂直于过切点的半径温故而知新探究:如图:PA为⊙O的一条切线,沿着直线PO将图形对折,设圆上与点A重合的点为B,这时OB是⊙O一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性说明图中的PA与PB,∠APO与∠BPO有什么关系?PABOOB也是的⊙O半径,PB也是切线,
PA=PB ,∠APO=∠BPO ,ABPO经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.∵PA,PB是⊙O的两条切线∴OA⊥AP,OB⊥BP又OA=OB,OP=OP,∴Rt△AOP≌Rt△BOP.∴PA=PB,∠OPA=∠OPB切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.平分切点所成的两弧,垂直平分切点所成的弦.已知,如图,PA、PB是⊙O的两条切线,
A、B为切点.直线 OP 交 ⊙O 于点 D、E,
交 AB 于 C.
(1)写出图中所有的垂直关系;
(2)写出图中所有的全等三角形.
(3)如果 PA = 4 cm , PD = 2 cm ,
求半径 OA的长.例1例1解:(1) OA⊥PA , OB⊥PB , OP⊥AB(2) △OAP ≌△ OBP , △OCA≌△OCB ,
△ACP≌△BCP.(3) 设 OA = x cm , 则 PO = PD + x = (2 + x )cm 在 Rt△OAP 中,由勾股定理,得 PA 2 + OA 2 = OP 2 即 4 2 + x 2 = (x + 2 ) 2 解得 x = 3 所以,半径 OA 的长为 3 cm. 思考 如图,一张三角形的铁皮,如何在它上面截下
一块圆形的用料,并且使圆的面积尽可能大呢?ID已知:△ABC
求作:⊙I使它与△ABC各边都相切作法:(1)作B,C的平分线,BM,CN.设它们
相交于点I.
(2)过点I作ID⊥BC,垂足为D.
(3)以点I为圆心,ID为半径作⊙I
则⊙I即为所求.内切圆和内心的定义:与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫
做三角形的内心.
这个三角形叫做圆的
外切三角形有关概念例2 △ABC的内切圆⊙O与BC、CA、AB分别相切
于点D、E、F,且AB=9cm,BC=14cm,
CA=13cm,求AF、BD、CE的长.解:设AF=x(cm),则AE=x(cm)∴CD=CE=AC-AE=13-x
BD=BF=AB-AF=9-x由 BD+CD=BC可得
(13-x)+(9-x)=14解得 x=4∴ AF=4(cm), BD=5(cm), CE=9(cm).练习:P106:1.2作业:P110:5,11,12记忆:1. Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半径是_______.11.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.F2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC于点D,试判断△AED的形状,并
说明理由.基础题:1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O边长为2cm的正方形ABCD的内切圆,E、F切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.EFHG正方形22cm2cm4.已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)图甲,AB为直径,要使得EF是⊙O切线,还需添加的条件
(只需写出三种情况)①___________②_____________
③______________.
(2)图乙, AB为非直径的弦,∠CAE=∠B.求证:EF是⊙O的
切线.∠CAE=∠BAB⊥FE∠BAC+∠CAE=90°H5.小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用图乙,说
明她这样做的道理.1、已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,以腰DC的中点 E 为圆心的圆与 AB 相切,梯形的上底 AD 与底 BC 是方程 x 2-10x + 16 = 0 的两根,求 ⊙E 的半径 r .F想一想:圆的外切四边形的两组对边有什么关系?说明你的结论的正确性.ABCDOLMNP谢谢大家的合作!
祝大家学习进步,万事如意!
同课章节目录
