1.1.2空间向量的数量积运算 课件(共14张PPT)
文档属性
| 名称 | 1.1.2空间向量的数量积运算 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-08 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
延时符
复习巩固
1
2
3
当
当
当
A
B
C
O
A
O
Q
P
M
N
与平面向量一样,空间向量的线性运算满足以下运算律(其中λ,μ∈R):
交换律: ;
结合律: ;
分配律:(λ+μ)=+μ ,
(a+b)=+.
延时符
第一章 空间向量与立体几何
1.1.2空间向量的数量积运算
授课人:张龙吉 日期:2023年8月7日
学 习 目 标
延时符
掌握空间向量的夹角的概念,培养数学抽象的核心素养.
3
掌握空间向量的数量积的定义、性质、运算律,提升数学抽象的核心素养.
了解空间向量投影的概念以及投影向量的意义,培养直观想象的核心素养.
能用空间向量的数量积解决立体几何中的垂直、夹角、长度等问题,强化数学运算的核心素养.
4
延时符
新课导入
如图,已知两个非零向量,在空间任取一点O,作=,=则∠AOB叫做向量的夹角,记作.
O
B
A
O
B
A
如果=,那么向量互相垂直,记作.
一 空间向量的夹角
5
延时符
新课知识
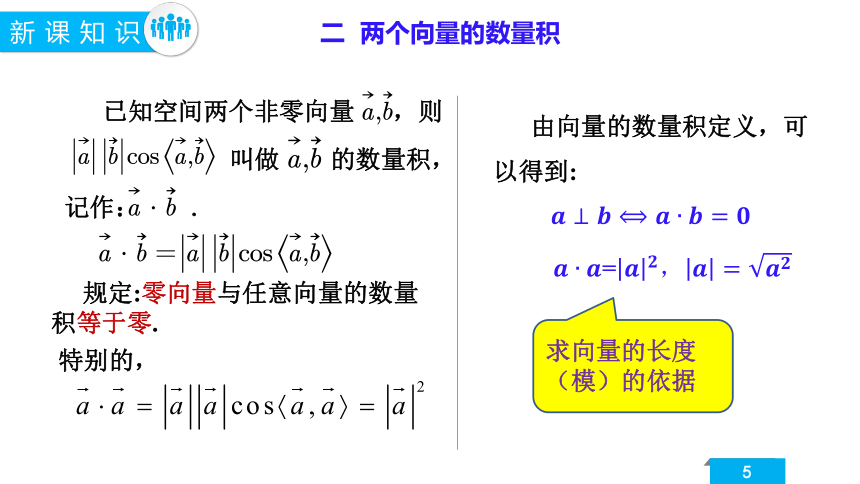
规定:零向量与任意向量的数量积等于零.
特别的,
二 两个向量的数量积
已知空间两个非零向量 ,则
叫做 的数量积,
记作: .
由向量的数量积定义,可以得到:
=
求向量的长度(模)的依据
6
延时符
新课知识
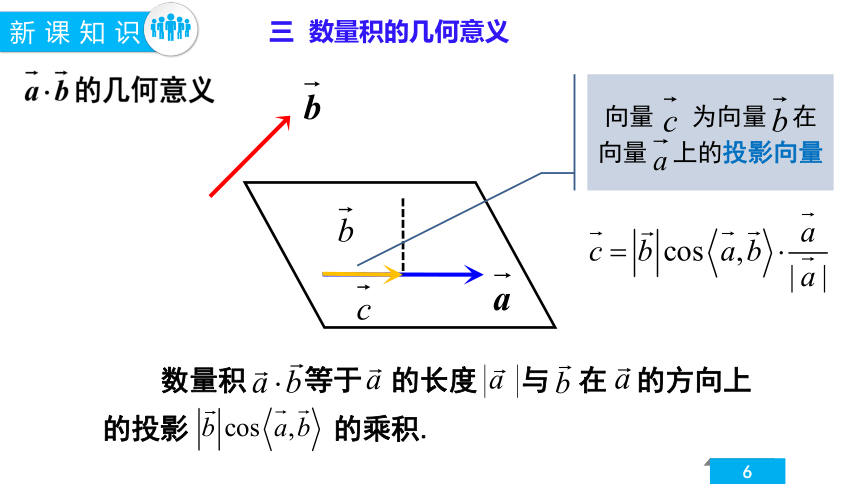
数量积 等于 的长度 与 在 的方向上的投影 的乘积.
向量 为向量 在向量 上的投影向量
三 数量积的几何意义
7
延时符
例题精讲
四 空间向量数量积的运算
空间向量的数量积满足如下的运算律:
()·=(·),∈R
·=·(交换律)
·(+)=·+· (分配律)
8
延时符
例题精讲
A
B
C
D
9
延时符
例题精讲
10
延时符
例题精讲
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
l
m
n
g
11
延时符
例题精讲
l
m
n
g
12
延时符
课堂小结
1. 本节课学习的概念有哪些?
2. 在解决问题时,用到了哪些数学思想?
本课作业
必做 二
必做 一
必做 三
教材 9 页
习题 1.1 4
教材 10页
习题1.1 7~10
2
01
02
03
谢
谢
聆
听
作者:梅河口市朝鲜族中学
2023年8月7日
延时符
复习巩固
1
2
3
当
当
当
A
B
C
O
A
O
Q
P
M
N
与平面向量一样,空间向量的线性运算满足以下运算律(其中λ,μ∈R):
交换律: ;
结合律: ;
分配律:(λ+μ)=+μ ,
(a+b)=+.
延时符
第一章 空间向量与立体几何
1.1.2空间向量的数量积运算
授课人:张龙吉 日期:2023年8月7日
学 习 目 标
延时符
掌握空间向量的夹角的概念,培养数学抽象的核心素养.
3
掌握空间向量的数量积的定义、性质、运算律,提升数学抽象的核心素养.
了解空间向量投影的概念以及投影向量的意义,培养直观想象的核心素养.
能用空间向量的数量积解决立体几何中的垂直、夹角、长度等问题,强化数学运算的核心素养.
4
延时符
新课导入
如图,已知两个非零向量,在空间任取一点O,作=,=则∠AOB叫做向量的夹角,记作.
O
B
A
O
B
A
如果=,那么向量互相垂直,记作.
一 空间向量的夹角
5
延时符
新课知识
规定:零向量与任意向量的数量积等于零.
特别的,
二 两个向量的数量积
已知空间两个非零向量 ,则
叫做 的数量积,
记作: .
由向量的数量积定义,可以得到:
=
求向量的长度(模)的依据
6
延时符
新课知识
数量积 等于 的长度 与 在 的方向上的投影 的乘积.
向量 为向量 在向量 上的投影向量
三 数量积的几何意义
7
延时符
例题精讲
四 空间向量数量积的运算
空间向量的数量积满足如下的运算律:
()·=(·),∈R
·=·(交换律)
·(+)=·+· (分配律)
8
延时符
例题精讲
A
B
C
D
9
延时符
例题精讲
10
延时符
例题精讲
由于空间向量的线性运算和数量积运算具有鲜明的几何背景,空间图形的许多性质可以由向量的线性运算及数量积运算表示出来,因此,立体几何中的许多问题可以用向量运算的方法加以解决.
l
m
n
g
11
延时符
例题精讲
l
m
n
g
12
延时符
课堂小结
1. 本节课学习的概念有哪些?
2. 在解决问题时,用到了哪些数学思想?
本课作业
必做 二
必做 一
必做 三
教材 9 页
习题 1.1 4
教材 10页
习题1.1 7~10
2
01
02
03
谢
谢
聆
听
作者:梅河口市朝鲜族中学
2023年8月7日
